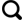1 引 言
影像匹配问题的提出是在20世纪70年代,经过多年发展,相关匹配方法和策略也被大量提出,逐渐成为影像处理分析中各个领域的研究热点和重点,同时也是最基础、应用最广泛的技术之一 [8] 。Le Moigne等 [9, 10, 11] 采用Wavelet特征实现了遥感影像的自动匹配。Dawn等 [12, 13, 14] 对遥感影像的匹配方法和应用进行了总结和综述。对于卫星摄影测量来说,最小二乘匹配 [15] 、跨接法影像匹配 [15] 和几何约束的互相关算法 [16] 等已成为多视三维重建和数字表面模型生成等应用的主流匹配方法。其中,最小二乘影像匹配是以局部范围影像灰度值作为匹配实体,以搜索窗口中心位置为待定参数,使模板窗口和搜索窗口的灰度值差的平方和最小,从面确定共轭实体 [17] 。而相位相关影像匹配的理论基础是傅里叶变换的卷积定理和平移特性。相关研究有:Kuglin等 [18] 提出了正像素级相位相关方法;Tzimiropoulos等 [19] 提出了以影像梯度为影像表达的梯度相关;Ojansivu等 [20] 对相位相关匹配性能进行了分析。
由于最小二乘匹配和相位相关匹配等都有其各自的局限性,本文首先选用SIFT匹配算法进行粗匹配,然后采用以最小二乘和相位相关匹配在序列影像窗口下对粗匹配的同名点对进行纠正,并计算和比较相关系数测度,以相关系数的大小作为衡量同名匹配正确与否的指标,选择相关系数最大的匹配结果来作为最终的结果,通过实验验证本方法能够对粗匹配的同名点对进行匹配纠正,提高匹配准确度。
2 影像匹配算法
2.1 SIFT匹配
SIFT匹配算法( 图1)最早是由David Lowe于1999年提出,其主要思想是将图像之间的匹配转化为特征向量之间的匹配 [ 21] 。首先通过对原始影像进行尺度变换,获得图像多尺度下的尺度空间表示序列,并对其进行主轮廓提取获取特征向量,然后通过比较每一个像素点与其相邻点寻找高斯差分金字塔的极值点,完成关键点初步检测。由于初步检测的关键点有很多点不稳定或者错误,因此需要对初步检测的关键点进行复筛,得到稳定关键点的精确点位,这也保证了关键点在尺度空间的不变性。但是当影像进行视角改变或者旋转时,稳定关键点不具有不变性。因此通过求解每个关键点的梯度方向进行方向赋值实现视角和旋转的不变性。然后对稳定关键点及其周围有贡献的临域点以数学公式的方式进行定义,从而确立左右影像的匹配实体的对应关系。
图1
2.2 最小二乘匹配法
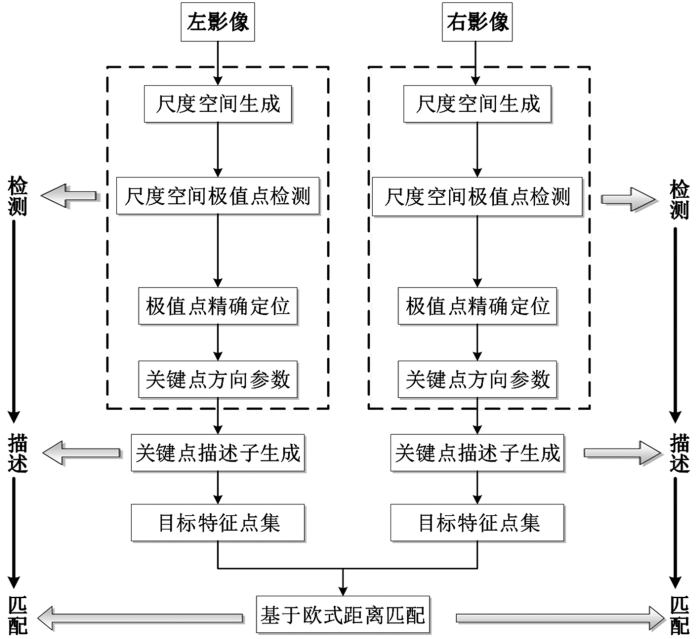
最小二乘匹配算法是灰度匹配算法中的典型算法,其是以协方差最小求解影像中几何畸变参数和辐射畸变参数,并以协方差最小作为迭代的条件最终使影像的误差平方和最小 [ 23] 。根据影像中的辐射畸变和几何畸变,将最小二乘匹配分为仅考虑辐射畸变的最小二乘匹配、仅考虑几何畸变的最小二乘匹配以及单点最小二乘匹配 [ 24] 。单点最小二乘匹配充分地考虑了影像的几何畸变和辐射畸变,其首先使用一定大小的匹配窗口,一般在一次多项式下进行几何变形的纠正,将左右影像的灰度阵列进行统一。然后对左影像相对右影像的线性灰度变形进行纠正。对于经过几何畸变纠正和辐射畸变纠正的立体像对,可以列出误差方程式并进行线性化,从而建立法方程求解出系统参数的改正数,并设定一定的阈值,作为求解的循环条件,直到计算出阈值之内的最佳匹配点位 [ 24, 29] ( 图2)。
图2
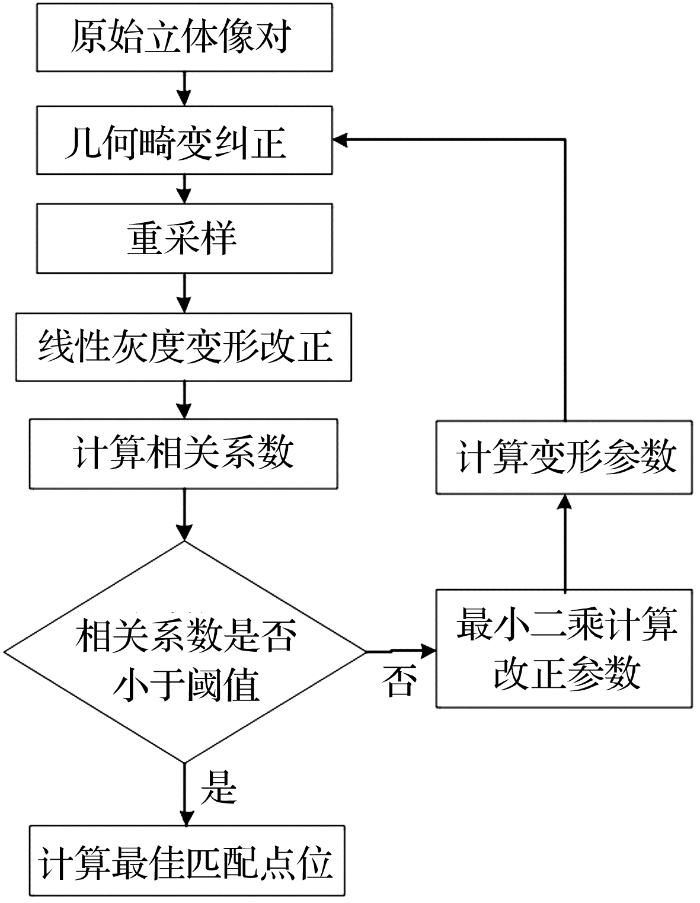
2.3 最小二乘匹配法
图3
2.4 本文算法策略
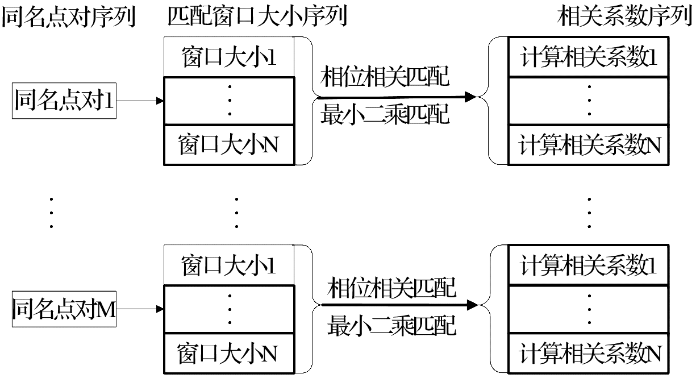
本文算法融合利用了最小二乘和相位相关匹配算法。一般来说,粗匹配结果是经过相关系数匹配等一系列方法得出,本文利用SIFT匹配 [ 27] 获得起始的粗匹配结果,作为后续匹配纠正的基础。粗匹配后会获得立体像对的若干对同名点,以其中每一对同名点作为基准,在原始立体像对的左右影像中分别开一个大小相同的匹配窗口。此匹配窗口在最小二乘和相位相关匹配中具有不同的作用,其中对于最小二乘算法来说,窗口是为了计算相关系数,而在相位相关匹配中,其目的在于计算同名像点的归一化互相关功率谱从而确定位移量。对于不同性质的原始影像来说,其在影像分辨率、影像成像方式、影像地面特征等方面存在很大的不同,采用不同的影像时应该选择不同大小的搜索窗口,并且匹配窗口的大小与立体像对的性质没有直接的规律,因此我们考虑对于粗匹配的每一个同名点对使用大小逐渐变化的序列窗口。以最小二乘和相位相关匹配在大小不同的序列影像搜索窗口下对sift算法初匹配后的同名点结果进行匹配纠正,并计算和比较相关系数测度,以相关系数测度的大小作为衡量同名匹配正确与否的指标,选择相关系数最大的匹配结果作为最终的结果。其主要策略如 图4所示。
图4
3 实验数据
本文实验数据来源于山西某区域,区域面积约8.9 km 2。此区域地处黄土高原,地形多样,丘陵、山地等共存,地面裸露区域较多,植被覆盖相对较简单。整个区域呈现西北、东南高,中间低,丘陵垣地为主。区域的海拔高度在400~800 m不等,其中北部区域海拔约680~750 m,相对高度250 m,中部和南部区域海拔约500~600 m,相对高度145 m。本区域气候呈现温带大陆性气候,昼夜温差较大,四季分明,年日照平均时数约2 450 h,年平均风速约2.0 m/s,年平均气温约8~15 ℃。因此针对无人机的特点和当地气候、降雨、日照、风速、季节等合理选择影像拍摄日期。
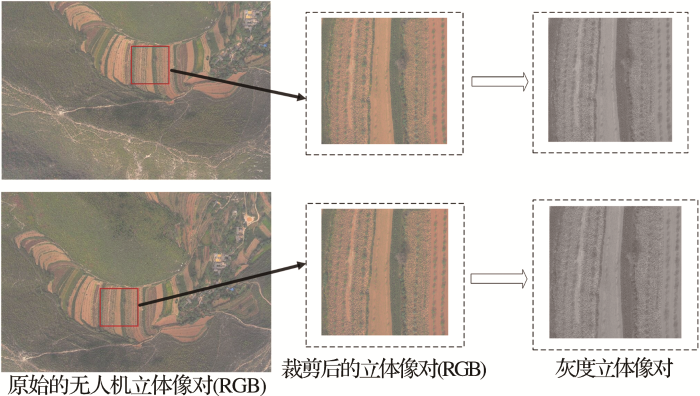
对于影像性质来说,本文选用的是基于固定翼的无人机影像,此影像由尼康D800-9002902于2017年10月23日下午4点左右于飞行高度735 m拍摄,无人机平台选用的武汉智能鸟KC-2000,坐标系采用的是CGCS2000坐标系,投影方式为高斯-克吕格投影。此次飞行相机的主要参数如下:相机焦距为36.054 99 mm,像元大小4.88 μm,像幅为7 360×4 912像素,相机的主点 x0为-0.096 mm,主点 y0为0.109 mm,检校时以影像中心为坐标原点, x轴向右, y轴向上。为了降低运算的复杂性,在原始的彩色立体像对上裁剪出一个1 000×1 000的区域,并且由于无人机影像为彩色三波段影像,将裁剪出来的彩色立体像对转换成灰度立体像对,如 图5所示,此裁剪区域地表相对平坦,地区简单。为了解决由于实验范围相对较小、实验区域地表平坦,地物简单所造成实验结果的偶然性,在区域北部高差大的区域裁剪出一个2 000×2 000的验证区域对上述区域的实验结果进行验证。本2 000×2 000区域相比1 000×1 000区域特点如下:地物更加复杂、裸露地块比例更低。区域高差大,属于北部山地区域,范围增加4倍。整个实验中,以1 000×1 000区域进行主导实验数据,以2 000×2 000的区域作为验证实验区域。
图5
图6
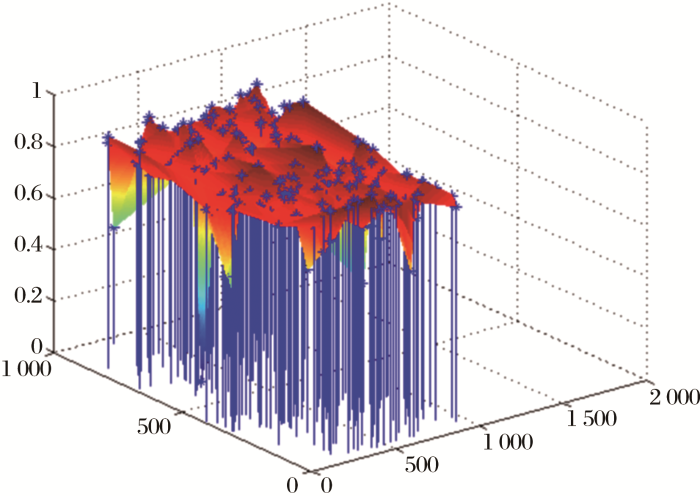
图6
sift粗匹配后的同名点对分布
Fig.6
The distribution of corresponding points after sift matching
图7
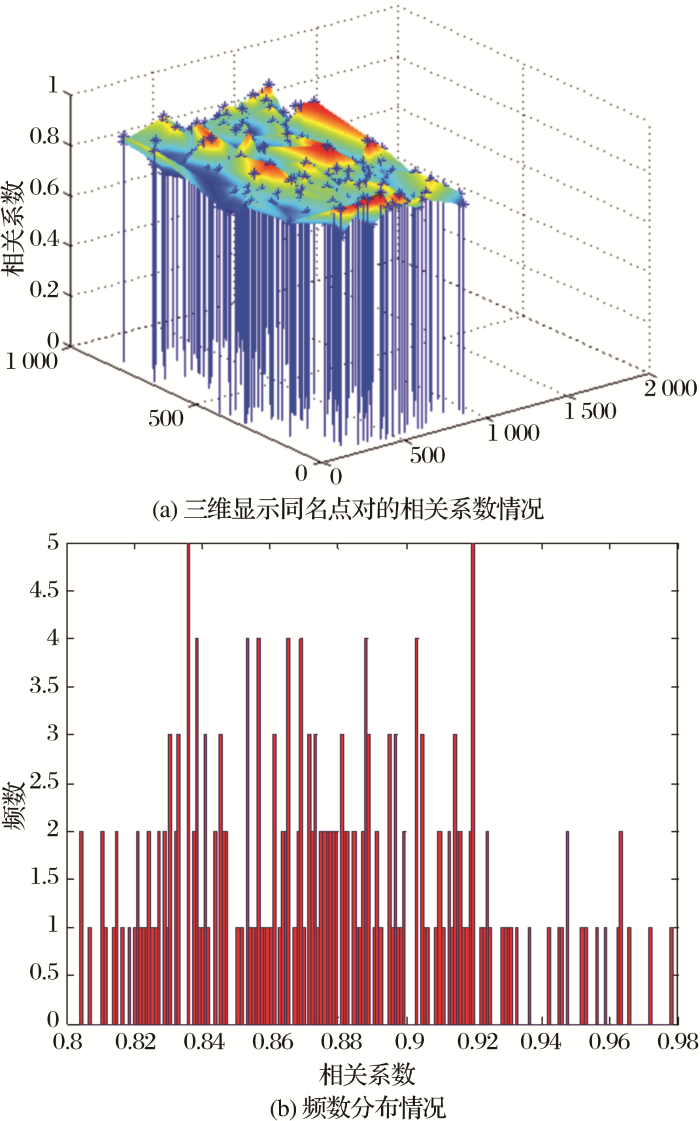
图7
相关系数介于0.8~1.0的同名点对频数分布
Fig.7
Frequency distribution of corresponding points whose correlation coefficients are ranging from 0.8 to 1.0
4 实验与分析
基于此基础数据,主要的实验方案如 表1所示。
表1 主要实验方案
Table 1
| 方案 | 误匹配剔除方法 | 序列窗口 |
|---|---|---|
| A | 单独最小二乘 | 否 |
| B | 单独相位相关 | 否 |
| C | 单独最小二乘 | 是 |
| D | 单独相位相关 | 是 |
| E | 融合最小二乘和相位相关 | 是 |
4.1 固定窗口下单独使用最小二乘
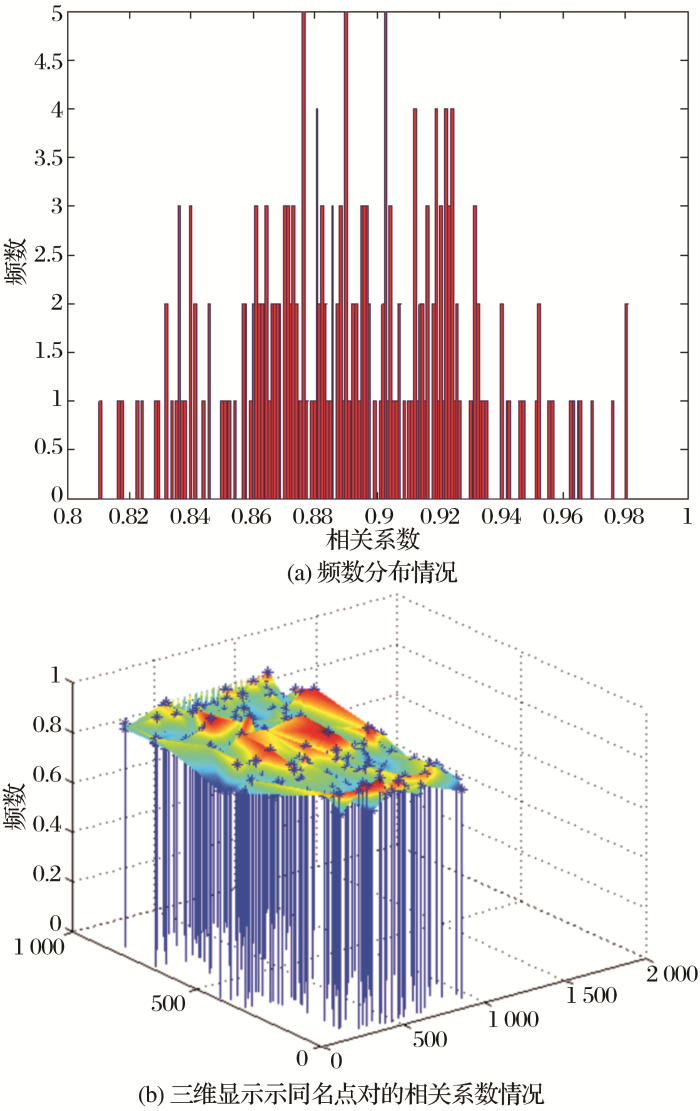
在固定窗口下单独使用最小二乘对粗匹配结果进行精化,精化后的同名点对为211对,其中相关系数介于0.8~0.9的有124对,相关系数介于0.9~1.0的有87对。 图8为在不使用序列窗口单独使用最小二乘的频数分布和相关系数显示情况。
图8
图8
在不使用序列窗口下单独使用最小二乘
Fig.8
Distribution of corresponding points after using Least Squares in fixed windows
4.2 在不使用序列窗口下单独相位相关
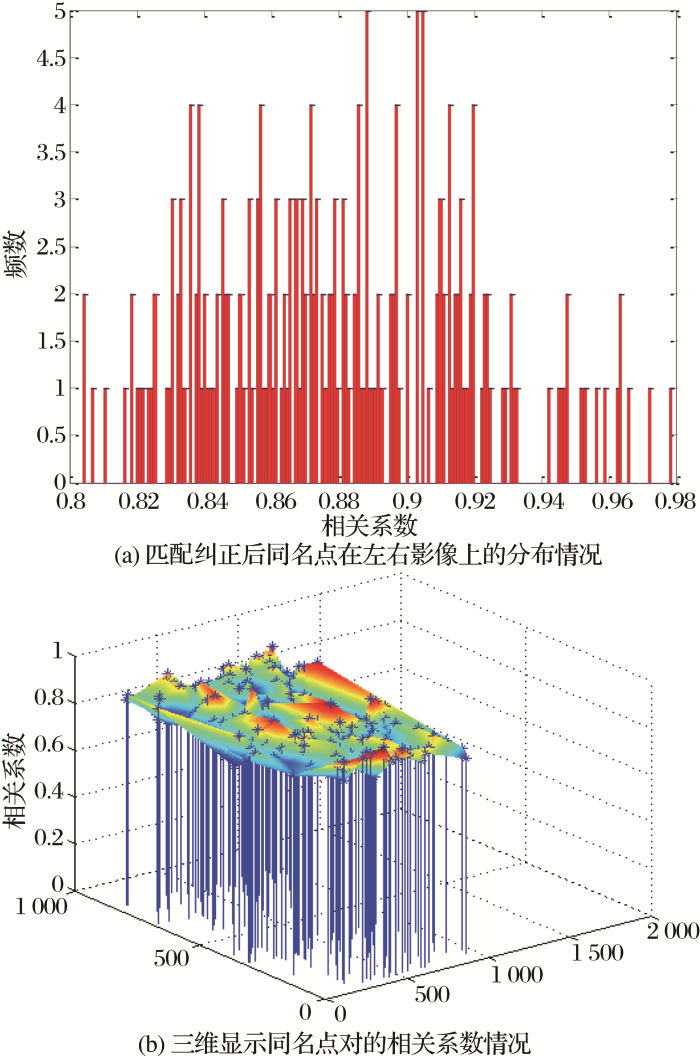
如 图9在不使用序列窗口下单独使用相位相关的同名点对的分布和相关系数情况,在固定窗口下单独使用相位相关对粗匹配结果进行精化,精化后的同名点对为211对,其中相关系数介于0.8~0.9的有144对,相关系数介于0.9~1.0的有67对。
图9
图9
在不使用序列窗口下单独使用相位相关
Fig.9
Distribution of corresponding points after using Phase Correlation in fixed windows
4.3 在序列窗口下单独最小二乘
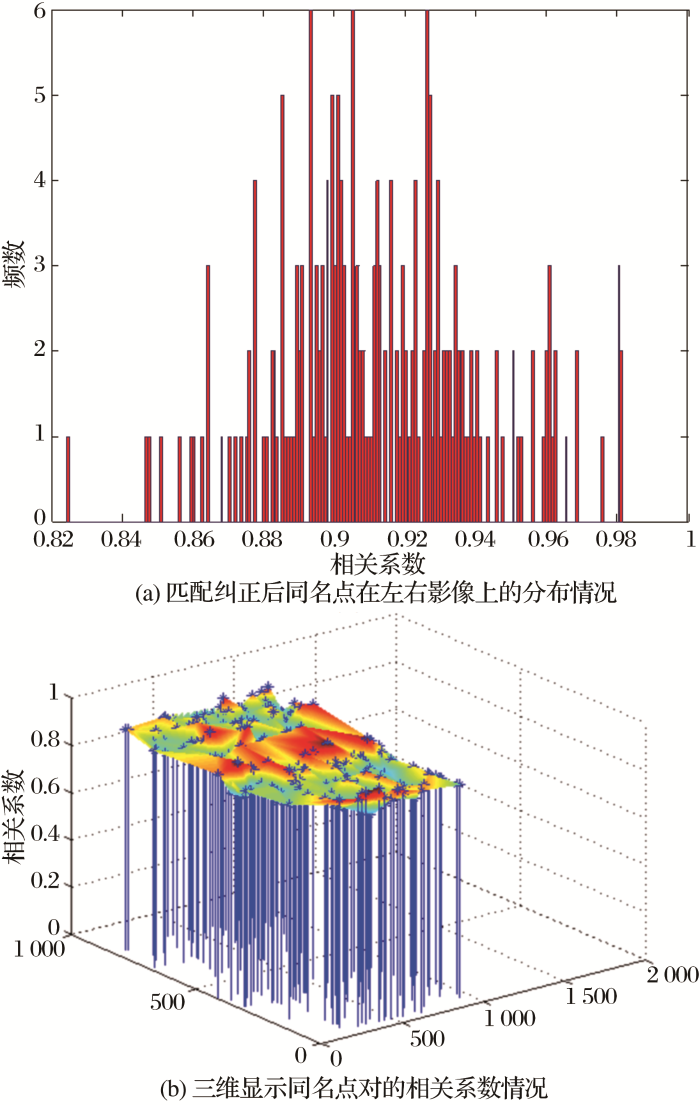
在序列窗口下单独使用最小二乘对粗匹配结果进行精化,精化后同名点对为211对,其中相关系数介于0.8~0.9的有71对,相关系数介于0.9~1.0的有140对。 图10为在序列窗口下单独使用最小二乘的频数分布和相关系数显示情况。
图10
图10
在序列窗口下单独使用最小二乘
Fig.10
Distribution of corresponding points after using Least Squares in window series
4.4 在序列窗口下单独相位相关
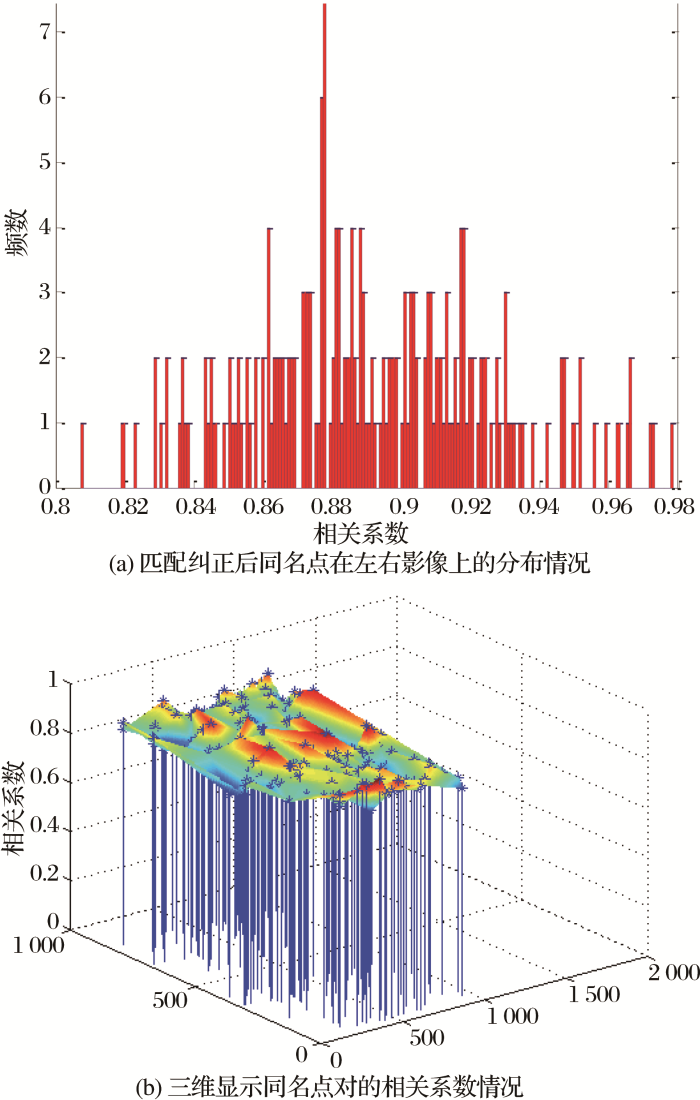
在序列窗口下单独使用相位相关对粗匹配结果进行精化,精化后同名点对为211对,其中相关系数介于0.8~0.9的有124对,相关系数介于0.9~1.0的有87对。如 图11在序列窗口下单独使用相位相关的同名点对的分布和相关系数情况。
图11
图11
在序列窗口下单独使用相位相关
Fig.11
Distribution of corresponding points after using Phase Correlation in window series
4.5 本文序列窗口下融合最小二乘和相位相关
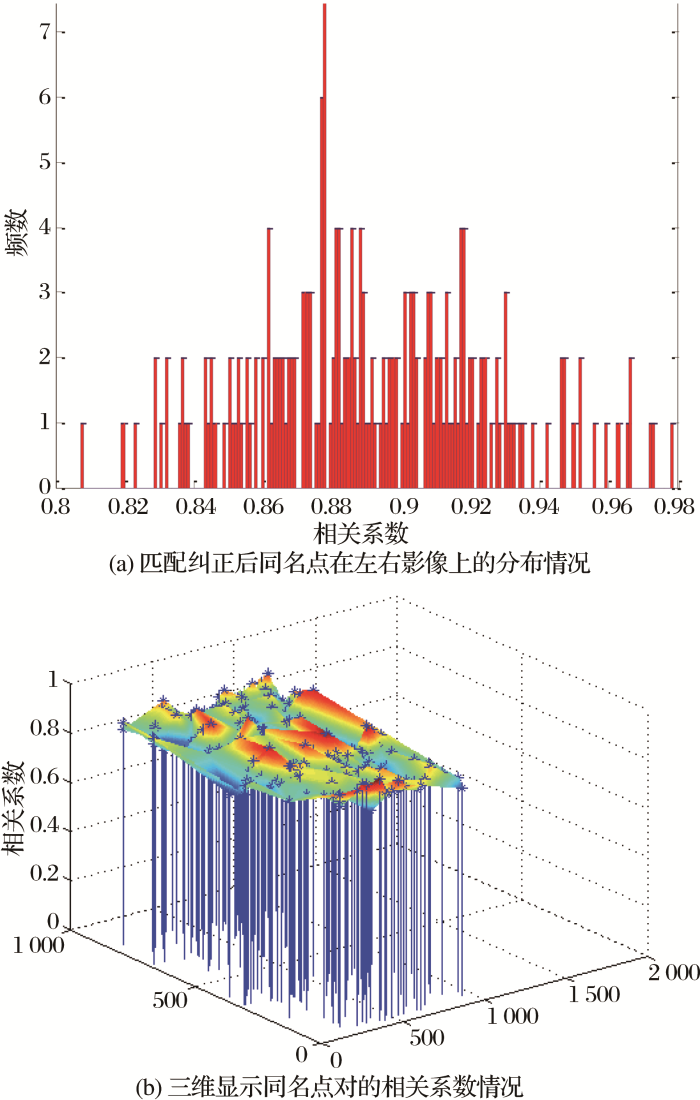
在序列窗口下融合最小二乘和相位相关对粗匹配结果进行精化,精化后的同名点对为211对,其中相关系数介于0.8~0.9的有65对,相关系数介于0.9~1.0的有146对。如 图12为本文序列窗口下融合最小二乘和相位相关的同名点在左右影像上的分布情况和相关系数情况。
图12
图12
本文序列窗口下融合最小二乘和相位相关
Fig.12
Distribution of corresponding points after Integrating Phase Correlation and Least Squares in window series
5 讨 论
上述实验后,几种方案下的同名点对总数为211对,实验结果如 表2所示,ρ为相关系数。主要分析如下:
表2 主要实验结果
Table 2
| 实验方案 | ρ∈[0.8,0.9] | ρ∈[0.9,1.0] |
|---|---|---|
| 基础数据 | 153 | 58 |
| 方案A | 124 | 87 |
| 方案B | 144 | 67 |
| 方案C | 71 | 140 |
| 方案D | 124 | 87 |
| 方案E | 65 | 146 |
(1)由实验方案,(A)和(B)方案分别是在不使用序列窗口下对基础数据单独进行最小二乘和相位相关,从实验结果看,基于单独最小二乘的匹配纠正后,相关系数介于0.9~1.0的同名点对由58对增加到87对,基于单独相位相关的匹配纠正后,相关系数介于0.9~1.0的同名点对由58对增加到67对。相较于基础数据,在此两种方法对基础数据进行匹配点纠正后,相关系数介于0.9~1.0的同名点对数都有了比较大的提升,其中基于单独最小二乘总体上要优于基于相位相关的匹配纠正。
(2)由实验方案(C)和(A),在序列窗口下进行最小二乘的匹配纠正后,相关系数介于0.9~1.0的同名点对由87对增加到140对,效果要优于在固定窗口下的匹配纠正。同理,将实验方案(D)与(B)比较,在序列窗口下进行单位相位相关的匹配纠正要远远优于在固定窗口下的匹配纠正。
将本文提出的基于序列窗口的融合最小二乘和相位相关与基础数据、实验方案(A)~(D)的结果进行比较,本文提出的方法将基础数据中相关系数介于0.9~1.0的同名点对由58对增加到146对,能够最好地对基础数据进行精化。
为了排除上述实验由于区域范围小、区域地表平坦,地物简单所造成实验结果的偶然性,采用北部区域裁剪的地物更加复杂、裸露地块比例更低、高差更大的2 000×2 000的山地区域数据执行上述实验步骤,进行实验验证。其基于2 000×2 000山地区域的实验结果如 表3所示。
表3 验证实验主要实验结果
Table 3
| 实验方案 | ρ∈[0.8,0.9] | ρ∈[0.9,1.0] |
|---|---|---|
| 基础数据 | 313 | 363 |
| 方案A | 167 | 509 |
| 方案B | 264 | 412 |
| 方案C | 114 | 562 |
| 方案D | 212 | 464 |
| 方案E | 69 | 607 |
从 表3可以看出:将本文提出的基于序列窗口的融合最小二乘和相位相关与基础数据、实验方案(A)~(D)的结果进行比较,本文提出的方法将基础数据中相关系数介于0.9~1.0的同名点对由363对增加到607对,能够最好地对基础数据进行精化。同时也是对1 000×1 000实验结果的验证,表明:在北部区域裁剪的地物更加复杂、裸露地块比例更低、高差更大山地区域,本方法的改进效果会更加明显。
6 结 语
本文以SIFT匹配后相关系数介于0.8~1.0的211对同名点对作为实验的基础数据,分别执行固定窗口下的单独最小二乘和单独相位相关、序列窗口下的单独最下二乘和单独相位相关以及本文提出的基于序列窗口的融合最小二乘和相位相关,主要结论如下:
(1) 无论是单独最小二乘还是单独相位相关,使用序列窗口能够明显地提升匹配精度。并且,在序列窗口和固定窗口下,单独最小二乘载总体上要优于基于相位相关的匹配纠正。
(2) 本文提出的基于序列窗口的融合最小二乘和相位相关能够有效地对粗匹配的同名点对进行纠正,其效果要优于序列窗口和固定窗口下单独进行最小二乘或相位相关。
本文提出的基于序列窗口的融合最小二乘和相位相关影像匹配算法与传统的最小二乘或相位相关匹配算法相比,能够极大地提高匹配点精度,达到精匹配的目的,并且对于地物地貌复杂、高差较大的山地区域也能取得比较好的效果,能够一定程度上为西部地区的成图作业提供帮助。但是毫无疑问,基于序列窗口匹配虽然能提高匹配点对的精化精度,但同时带来时间消耗的增加,这种劣势在大范围区域成图时必将带来大量时间浪费。因此针对更大规模和范围的无人机影像,如何加入并行化等策略,将是下一步研究的重点和核心。
参考文献
A Survey of Image Registration Techniques
[J].
Gradient Consistency Operator for Multimodal Image Registration
[J].
多模态图像配准的梯度一致性算子
[J].
3D Change Detection-approaches and Applications
[J].
Multi-Source Remote Sensing Data Fusion: Status And Trends
[J].
Multi-image Matching for DSM Generation from IKONOS Imagery
[J].
State of The Art in High Density Image Matching
[J].
Object-based Image Information Fusion Using Multisensor Earth Observation Data over Urban Areas
[J].
Image Registration Algorithm Based on Local Features and Its Application
[D].
基于局部特征的图像配准算法及应用研究
[D].
An Automated Parallel Image Registration Technique based on the Correlation of Wavelet Features
[J].
Image Registration for Remote Sensing
[M].
Remote Sensing Image Registration Techniques: A Survey
[C]∥
Development and Status of Image Matching in Photogrammetry
[J].
Use of Multiresolution Wavelet Feature Pyramids for Automatic Registration of Multisensor Imagery
[J].
Digital Image Correlation: Performance and Potential Application in Photogrammetry
[J].
High Precision Automatic Registration of Remote Sensing Image
[J].
遥感影像的高精度自动配准
[J].
Adaptive Least Squares Correlation: a Powerful Image Matching Technique
[J].
"A Generalized Conjugate Gradient, Least Square Method
[J].
The Phase Correlation Image Alignment Method
[C]∥Proceedings of the International Conference on Cybernetics and Society,
Robust Fft-Based Scale-invariant Image Registration with Image Gradients
[J].
Image Registration Using Blur-Invariant Phase Correlation
[J].
SIFT: Predicting Amino Acid Changes That Affect Protein Function
[J].
The Realization and Research of Correlation Coefficient and Least Square Image Matching Algorithm
[J].
相关系数和最小二乘影像匹配算法的实现与研究
[J].
A Novel Sub-pixel Phase Correlation Method Using Singular Value Decomposition and Unified Random Sample Consensus
[J].
A Sub-pixel Image Matching Technique Using Phase-only Correlation
[C]∥International Symposium on Intelligent Signal Processing and Communications,
Extension of Phase Correlation to Subpixel Registration
[J].
Improved Video Stabilization Using Sift-Log Polar Technique for Unmanned Aerial Vehicles
[C]∥
The Extension of Phase Correlation To Image Perspective Distortions based on Particle Swarm Optimization
[J].
Weighted Least Square Method for Epipolar Rectification in Semi-Calibrated Image
[C]∥International Society for Optics and Photonics
Method for The Fpga-based Long Range Multi-View Stereo With Differential Image Rectification