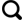由粗到细的高光谱图像多端元光谱混合分析

doi:10.11873/j.issn.1004-0323.2019.6.1305

由粗到细的高光谱图像多端元光谱混合分析

左成欢^,¹, 赵辽英¹, 陆海强², 厉小润^,³

1.杭州电子科技大学计算机应用技术研究所，浙江杭州 310018

2.嘉兴市恒创电力设备有限公司，浙江嘉兴 314033

3.浙江大学电气工程学院，浙江杭州 310027

A Corse-to-Fine Scheme for Multiple Endmember Spectral Mixture Analysis of Hyperspectral Images

Zuo Chenhuan^,¹, Zhao Liaoying¹, Lu Haiqiang², Li Xiaorun^,³

1.Institute of Computer Application Technology，Hangzhou Dianzi University，Hangzhou 310018，China

2.Jiaxing Hengchuang Electric Power Equipment Co. LTD，Jiaxing 314033，China

3.College of Electrical Engineering, Zhejiang University，Hangzhou 310027，China

通讯作者: 厉小润（1970-），男，浙江东阳人，研究员, 主要从事图像处理与模式识别方面的研究。E⁃mail: lxr@zju.edu.cn。

收稿日期: 2018-07-06 修回日期: 2019-10-25 网络出版日期: 2020-03-20

基金资助:

国家自然科学基金项目. 61671408. 61571170
教育部联合基金项目. 6141A02022314

Received: 2018-07-06 Revised: 2019-10-25 Online: 2020-03-20

作者简介 About authors

左成欢（1992-），女，安徽安庆人，硕士研究生，主要从事高光谱图像光谱混合分析方面的研究E⁃mail:2685119427@qq.com , E-mail：2685119427@qq.com

摘要

光谱可变性是影响高光谱图像光谱混合分析精度的重要因素，多端元光谱混合分析是解决该问题的有效手段。为了降低光谱混合分析时间复杂度的同时提高其精度，提出了一种由粗到细的多端元光谱混合分析算法，该算法首先基于扩展的端元集对每个像元进行全约束光谱混合粗分析，确定含所有地物的初始端元集，在此基础上进一步进行精细光谱混合分析，迭代光谱混合分析构建端元子集，最终根据重构误差变化量确定各个像元的最优端元集。实验结果表明:相比迭代光谱混合分析法和分层多端元光谱混合分析法，所提出的由粗到细的高光谱图像多端元光谱混合分析能有效降低算法反演丰度误差并改善计算效率。

关键词： 高光谱图像 ; 多端元 ; 光谱混合分析 ; 重构误差变化量

Abstract

Spectral variability is an important factor which influences the accuracy of spectral analysis in hyperspectral images. Multiple endmembers spectral mixture analysis is an effective method to solve this problem. In order to reduce the time complexity of spectral mixing analysis and improve the accuracy in the same time, a multiple endmember spectral mixture analysis algorithm based on corse-to-fine scheme is proposed. Based on the extended endmember set for each pixel, the proposed algorithm firstly make fully-constrained spectral mixing coarse analysis to determine the initial set of end-members containing all land cover material. On this basis, the algorithm further conducts fine spectral mixture analysis, iterative spectral mixture analysis to build end-member subsets and the optimal end-member set is finally determined according to the variation of reconstruction error. The experimental results show that compared with the iterative spectral mixture analysis method and the hierarchical multi-endmember spectral mixture analysis algorithm, the proposed algorithm reduces the error of inversion abundance and improves computational efficiency greatly.

Keywords： Hyperspectral images ; Multiple endmembers ; Spectral mixture analysis ; The variation of reconstruction error

PDF (5243KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

左成欢, 赵辽英, 陆海强, 厉小润. 由粗到细的高光谱图像多端元光谱混合分析. 遥感技术与应用[J], 2019, 34(6): 1305-1314 doi:10.11873/j.issn.1004-0323.2019.6.1305

Zuo Chenhuan, Zhao Liaoying, Lu Haiqiang, Li Xiaorun. A Corse-to-Fine Scheme for Multiple Endmember Spectral Mixture Analysis of Hyperspectral Images. Remote Sensing Technology and Application[J], 2019, 34(6): 1305-1314 doi:10.11873/j.issn.1004-0323.2019.6.1305

1 引言

高光谱成像技术以其光谱分辨率较高的特点受到国内外的广泛关注，高光谱图像广泛应用于食品安全监测、地质制图、植被调查、大气研究和环境监测，以及城市应用等多个领域。然而，由于地物的复杂多样性和传感器空间分辨率的限制，使得高光谱图像中存在大量的混合像元 ^{[1, 2]}。混合像元的存在严重影响后续图像处理的精度。为了提高高光谱应用效果，必须先进行光谱混合分析 ^{[3, 4]}，明确混合像元内包含的地物及其比例。光谱混合分析是高光谱遥感应用的关键问题之一。传统的光谱混合分析方法假定每类地物只有一种端元光谱，典型的方法有正交子空间投影法 ^[5]和各种最小二乘法，如非负约束最小二乘法、丰度全加约束的最小二乘法和全约束的最小二乘法（Fully Constrained Least Squares Linear Spectral Mixture Analysis ,FCLS） ^[6]。由于地物的复杂多样性和成像条件的影响，高光谱图像“同物异谱”和“异物同谱”现象普遍存在，同一种地物的纯像元光谱不一定完全相同，导致对所有像元用固定的端元集解混精度不高。近几年，国内外学者对考虑端元变异的光谱混合分析进行了研究，比较有代表性的工作主要有三方面：基于确定性模型，从多端元集中寻找每个像元的最优端元组合 ^{7, 8, 9]}；通过特征提取或波段选择降低光谱变异对解混结果的影响 ^{[10, 11]}；对光谱变异程度建模，基于统计模型进行光谱混合分析 ^{[12, 13, 14, 15]}。文献[16, 17]对基于确定性模型和基于统计模型的两种方法进行了比较研究，结果表明当某种地物面积较小时确定性模型的精度高于统计模型。本文主要研究基于确定性模型的多端元光谱混合分析方法。

Roberts等 ^[5]提出的多端元光谱混合分析(MESMA，Multiple Endmember Spectral Mixture Analysis)是目前应用最广泛的确定性模型法，该算法为每个像元生成端元类别和个数均可变的所有候选端元集合并求相应的丰度，选择重构误差最小为的端元集解混相应的像元。MESMA算法虽然精度相对较高，但是计算量大。为了降低计算量，Derek等提出了迭代光谱混合分析（ISMA,Iterative Spectral Mixture Analysis） ^[8]，对每个像元，通过迭代剔除丰度最小的端元生成候选端元集，再根据重构误差变化量确定最优端元集解混相应的像元，当端元集较大时，ISMA算法的计算量仍然比较大。赵春晖等 ^[9]在MESMA算法的基础上提出了基于分层的多端元光谱解混(HMESMA, Hierarchical Multiple Endmember Spectral Mixture Analysis）算法,对每个像元，根据每类端元的最大丰度选择单端元构成其初始单端元集，进而根据解混误差变化量再分层确定最优端元集,进一步降低了计算复杂度。HMESMA分层求解过程中没有结合丰度信息，而是每次根据光谱角距离近似判断最优端元组合，影响了解混精度。利用HMESMA的初始单端元确定方法，结合ISMA的迭代端元子集构建思想，本文提出了一种由粗到细的多端元光谱混合分析(CFSMA，Coarse-to-Fine Spectral Mixture Analysis)算法，兼顾了光谱混合分析的计算复杂度和精度。

2 多端元光谱混合分析模型

光谱混合本质上分为线性混合和非线性混合，由于结构简单、物理含义明确，线性混合模型是传统光谱混合分析中常用的模型 ^{[18, 19]}。

设 $x$ 为高光谱图像中的一个像元， $e_{i}$ 表示第 $i$ 条端元， $a_{i}$ 示第 $i$ 条端元在像元 $x$ 中的丰度， $M$ 是端元数量， $ε$ 代表误差分量，线性光谱解混模型为:

x = E a + ε^{k}

其中： $E = [e_{1}, e_{2}, \dots, e_{M}]$ ， $a = [a_{1}, a_{2}, \dots, a_{M}]^{T}$ 。

为了使得求解得到的丰度系数符合物理意义，更好地反映混合像元中各端元之间的真实情况，需要满足丰度全加约束和丰度非负约束 ^[6]两个限制条件:

非负约束： $a_{i} \geq 0$ (2)

全加约束： $\overset{M}{\sum_{i}} a_{i} = 1$ (3)

不考虑端元的可变性，每类地物一个端元集构成固定的端元矩阵，基于线性混合模型(1)~(3)，利用FCLS方法可以很好地实现光谱混合分析。

考虑端元可变性，每类地物含多个端元，构成一个端元子集。设 $n_{i}$ 为第 $i$ 类地物类内端元光谱数，第 $i$ 类端元子集为 $E_{i} = [e_{i 1}, e_{i 2}, \dots, e_{i n_{i}}]$ ,丰度子集为 $a_{i} = [a_{i 1}, a_{i 2}, \dots, a_{i n_{i}}]^{T}$ ，其中 $e_{i j}$ 表示第 $i$ 类地物内的第 $j$ 条光谱， $a_{i j}$ 为其相应丰度，则整个端元集可以表示为 $\overset{̆}{E} = [E_{1}, E_{2}, \dots, E_{M}]$ ，待求丰度矩阵为 $\overset{̆}{a} = [a_{1}^{T}, a_{2}^{T}, \dots a_{M}^{T}]^{T}$ ，则相当于对每个像元用一个扩展后的单端元集进行光谱混合分析，扩展的线性混合模型为:

x = \overset{̆}{E} \overset{̆}{a} + ε

满足非负约束 ${\overset{̆}{a}}_{i} \geq 0$ 和全加性约束 $\overset{N}{\sum_{i}} {\overset{̆}{a}}_{i} = 1$ ， $N = \overset{M}{\sum_{i = 1}} n_{i}$ 为 $\overset{̆}{E}$ 中总的端元数。

基于扩展的多端元矩阵 $\overset{̆}{E}$ ，可以利用传统的光谱混合分析方法求丰度，但多选端元对像元进行光谱混合分析会导致过拟合现象，虽然重构的误差可能减小，但是丰度误差会增大，导致丰度反演精度降低 ^[20]。

高光谱图像中，不同像元包含的端元类别与端元个数是不同的。已知多端元集 $E$ ，考虑每个像元的实际端元组成，定义端元选择变量:

q_{i j} = \{\begin{matrix} 0 ， \\ 1 ， \end{matrix} \begin{matrix} x 中 含 e_{i j} \\ x 中 不 含 e_{i j} \end{matrix}

其中: $i = 1,2, \dots, M$ , $j = 1,2, \dots, N_{i}$ 。

设 $a_{i j}$ 表示第 $i$ 类地物内的第 $j$ 个光谱像元 $x$ 中所占的比例，基于线性光谱混合模型提出多端元光谱混合分析模型为:

x = \overset{M}{\sum_{i = 1}} \overset{N_{i}}{\sum_{j = 1}} q_{i j} a_{i j} e_{i j} + ε

其中： $\overset{M}{\sum_{i = 1}} \overset{N_{i}}{\sum_{j = 1}} q_{i j} a_{i j} = 1, 0 \leq a_{i j} \leq 1$ 。

基于模型（5）和（6）进行多端元光谱混合分析，首先通过一定的方法确定像元 $x$ 的端元选择变量 $q_{i j}$ 的值，根据端元选择变量从多端元集 $E$ 中选择 $q_{i j} = 1$ 对应的端元构成端元子集，并求取相应的丰度值。因此，基于确定性模型的多端元光谱混合分析就是端元子集选择与传统光谱混合分析的结合，如何选择端元子集是多端元光谱混合分析的关键。

3 CFSMA算法

3.1　算法描述

由粗到细的多端元光谱混合分析算法的基本思想是:首先用所有端元构成端元矩阵，对像元进行一次非精细的光谱混合分析，根据求得的丰度确定一个包含每类地物的初始端元集；然后基于初始端元集对像元进行精细光谱混合分析，确定其最优端元集和丰度。算法流程如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 CFSMA算法流程图

Fig.1 CFSMA algorithm flow chart

CFSMA算法过程及分析如下:

（1）光谱混合粗分析。根据公式（4），利用扩展的多端元矩阵 $\overset{̆}{E} = [E_{1}, E_{2}, \dots, E_{M}]$ (可以由光谱库中得到或者利用多端元提取算法从高光谱数据中提取)，　对高光谱数据 $x$ 求丰度，其中 $E_{i} = [e_{i 1}, e_{i 2}, \dots, e_{i n_{i}}]$ 表示第 $i$ 类内端元集合。考虑全加性和非负性约束，用全约束最小二乘法得到丰度向量 $\overset{̆}{a} = [a_{1}^{T}, a_{2}^{T}, \dots a_{M}^{T}]^{T}$ 。由于丰度最大的端元光谱最有可能是混合像元中包含的地物光谱，从每类端元子集 $E_{i}$ 中选取丰度最大的端元，构成初始端元集 ${\hat{E}}_{1}$ ，即:

{\hat{E}}_{1} = \{e_{i, a r g m a x (a_{i})}\} ， i = 1,2, \dots, M

(7)

（2）光谱混合细分析。光谱混合细分析的具体步骤如下：

Step1 初始化迭代次数 $t = 1$ 。

Step2 以 ${\hat{E}}_{t}$ 为端元集，用全约束最小二乘求丰度 ${\hat{a}}_{t}$ ，并计算重构误差：

r_{t} = \sqrt[]{{‖x - {\hat{E}}_{t} {\hat{a}}_{t}‖}_{2}^{2} / L}

(8)

其中: $L$ 表示波段数。

Step3 令 $k = a r g m i n ({\hat{a}}_{t})$ ，从 ${\hat{E}}_{t}$ 中去除第 $k$ 个端元，得到端元子集 ${\hat{E}}_{t + 1}$ ，更新 $t = t + 1$ 。

Step4 如果 ${\hat{E}}_{t}$ 中端元数大于1，则转Step2，否则， $r_{t} = \sqrt[]{{‖x - {\hat{E}}_{t}‖}_{2}^{2} / L}$ ， ${\hat{a}}_{t} = 1$ ，转Step5。

Step5 设定阈值 $T$ ，从 $i = ２$ 开始计算相连两次迭代的重构误差变化量:

∆ r_{i} = \frac{|r_{i} - r_{i - 1}|}{r_{i}}

(9)

如果 $∆ r_{i} > T$ ，则停止计算，结果 $x = {\hat{E}}_{i} {\hat{a}}_{i}$ ；否则如果 $i = Ｍ$ ，结果 $x = {\hat{E}}_{Ｍ} {\hat{a}}_{Ｍ}$ ；否则 $i = i ＋ 1$ ，重复计算公式(9)。

有3点需要说明：

(1)算法过程中的多次丰度求解必须满足全加性和非负性，因此选用全约束最小二乘。因为同类端元间通常光谱角距离很小（形状相似），但光谱值呈一定的比例，如果直接用不满足约束条件的最小二乘，不能保证丰度最大的端元最有可能是混合像元中包含的端元，也不能保证丰度最小的最不可能是端元。举个简单的例子，比如第一类地物的3个端元间满足关系： $e_{11} = 2 e_{12}$ ，像元 $x$ 的真实混合情况为 $x = 0.5 e_{11} + 0.5 e_{22}$ ，如果不考虑全加性约束条件，则 $x = 0.1 e_{11} + 0.8 e_{12} + 0.5 e_{22}$ 同样成立，丰度最大的 $e_{12}$ ，丰度最小的为 $e_{11}$ ，与实际不符。

(2)高光谱图像中大多数像元是由部分地物混合而成的，用包含所有地物的初始端元集对像元进行光谱混合粗分析，可能因为过拟合导致丰度反演精度下降 ^[7]，因此，需要进一步进行精细光谱分析，从 ${\hat{E}}_{1}$ 中找出冗余端元并去除，但是冗余端元的个数是未知的，因此需要迭代产生各种端元数的端元子集。

(3)光谱混合分析过程中，如果端元集中少一个实际端元，结果像元重构误差会明显变大，而冗余端元参与光谱解混，会导致过拟合现象，虽然重构误差减小了，但是丰度误差会增大，导致丰度反演精度降低 ^{[6, 7, 19]}。因此，直接根据重构误差不能准确反映光谱混合分析结果的优劣，根据重构误差变化量确定最优端元集比较合适。

3.2　算法时间复杂度分析与比较

为了便于描述，将含 $n$ 个端元的端元集求丰度的模型称为 $n$ -端元模型，一次 $n$ -端元模型运行时间记为 $T_{n}$ 。多端元光谱解混算法的解混端元模型数目由高光谱数据中包含 $M$ 类地物以及每类地物的类内端元数目 $n_{i}$ 决定。

以 $M = 4$ 类地物，每类地物含有的类内光谱个数 $n_{i}$ 都等于3，即: $E = {A 1, A 2, A 3, B 1, B 2, B 3, C 1,$

$C 2, C 3, D 1, D 2, D 3}$ 为例，比较分析各种多端元光谱混合分析算法的运行时间。

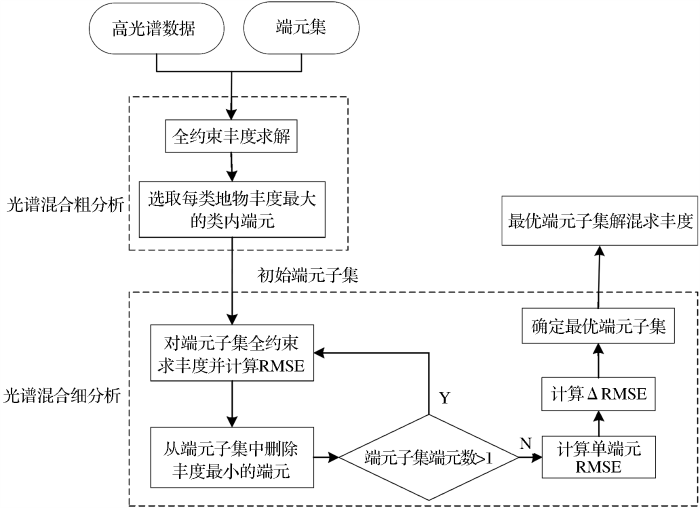
假设CFSMA算法对像元 $x$ 进行光谱分析的初始端元集为 ${\overset{́}{E}}_{1} = {A 1, B 1, C 1, D 1}$ ，迭代过程中依次删除端元 $D 1$ 、 $C 1$ ,和 $B 1$ ,其端元集构造过程如图2所示，则CFSMA算法的4-端元模型为1个，3-端元模型为1个，2-端元模型为1个，运行时间为 $T_{12} + T_{4} + T_{3} + T_{2} + T r s$ ，其中 $T r s$ 表示CFSMA算法中像元重构误差及变化量计算时间。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 CFSMA算法解混示意图

Fig.2 Schematic diagram of CFSMA unmixing algorithm

对于MESMA算法通过穷尽所有的端元组合模型，即4-端元模型为81个，2-端元模型为54个，3-端元模型为108个，运行时间为 $T_{12} + 81 \times T_{4} + 108 \times T_{3} + 54 \times T_{2} + T_{r M}$ ， $T_{r M}$ 表示MESMA算法中重构误差及变化量计算时间。

相比于MESMA算法，HMESMA算法通过考虑端元类别和端元个数分层寻找最优端元组合，而不必同时考虑端元类别和端元个数，即4-端元模型为1个，2-端元模型为3个，3-端元模型为2个，运行时间为 $T_{12} + T_{4} + 2 \times T_{3} + 3 \times T_{2} + T_{r M}$ ， $T_{r M}$ 表示HMESMA算法中重构误差及变化量计算时间。

而ISAM解混算法共有12个端元，因此有12个模型，运行时间为 $T_{12} + T_{11} + T_{10} + T_{9} + T_{8} + T_{7} + T_{6} + T_{5} + T_{4} + T_{3} + T_{2} + T_{1} + T_{r M}$ ， $T_{r M}$ 表示ISMA算法中重构误差及变化量计算时间。

根据上述分析可知，CFSMA端元组合模型个数远远小于MESMA、ISMA,以及HMESMA。对于 $M$ 类地物，每类地物的类内端元数目 $n_{i}$ 的情况，MESMA算法的M-端元模型数就有 $\overset{M}{\prod_{i = 1}} n_{i}$ ，其他模型数也有不少，随着端元个数和类内端元数的增加，MESMA算法的时间复杂度很高。ISMA算法的端元模型数从 $\overset{M}{\sum_{i = 1}} n_{i}$ 逐一减1，一直到2-端元模型，因此总的端元数增大，ISMA算法复杂度也变高。而CFSMA和HMESMA算法都是只做一次 M-端元模型分析，后续运算降为更低的端元模型，因此，总的端元个数对这两种算法时间复杂度的影响不大，并且总的模型数CFSMA最少。

4 实验结果与分析

为了验证改进算法的有效性，采用真实数据和模拟数据进行仿真实验，并将本文提出的CFSMA算法与sSMA ^[15]、HMESMA ^[6] 、ISMA ^[7] 3种算法做对比实验。为了评价高光谱混合像元解混的精度，主要采用定性和定量两种方法作为评价指标，定性分析采用求解得到的丰度图，即各个端元光谱在高光谱图像各个像元中所占的比例系数，用二维灰度图直观地显示，灰度图像越亮表示这种地物在该像元所占的比例系数越大，越暗表示这种地物在该像元所占的比例系数越小，每种地物都有相应的一幅解混分量图。而定量分析能在数值上分析解混的准确性，采用的定量分析方法是:丰度均方根误差RMSE。RMSE值越小代表解混效果越好，公式如下：

R M S E = \sqrt[]{\sum_{i = 1}^{N} {‖S_{i} - {\hat{S}}_{i}‖}_{2}^{2} / N}

其中 $: S_{i}$ 表示第 $i$ 个像元解混得到的丰度值; ${\hat{S}}_{i}$ 表示第 $i$ 个像元的真实丰度值; $N$ -代表总的像元个数。

4.1　仿真数据实验

分别做3组实验来验证算法的有效性。

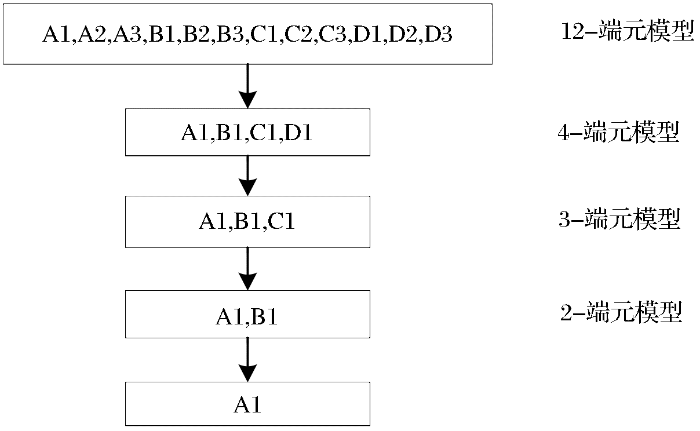
仿真实验1：仿真高光谱的数据，从美国地质勘探局USGA的矿物光谱库中选取4种矿物，分别为明矾石(Alunite)、橄榄石(Olivine)和绿泥石(Chlorite), 白云母(Muscovite)，每类矿物选取4条类内光谱，明矾石选取4条类内光谱分别用 A1、 A2、 A3、 A4表示，橄榄石选取4条类内光谱分别用 B1、 B2、 B3、 B4表示，绿泥石选取4条类内光谱分别用 C1、 C2、 C3、 C4表示，白云母选取4条类内光谱分别用 D1、 D2、 D3、 D4表示，各类地物端元光谱曲线如图3所示, 16种光谱合成大小为50×100的高光谱图像，其中有224个波段，仿真高光谱的第3波段合成数据如4所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 4类端元光谱曲线

Fig.3 Spectra of four endmenbers

合成高光谱图像方式：第1~50行、第1~20列，端元 A1、 B1以随机的比例系数合成，第1~50行、21~30列，端元 C1、 D1以随机的比例系数合成，第1~50行，31~50列，端元 A2, B2, C2以随机的比例系数合成，第1~50行，51~70列，端元 A3、 B3、 D2以随机的比例系数合成，第1~50行，71~90列，端元 A4、 B4、 C2、 D3以随机的比例系数合成, 第1~50行，91~100列，端元 C4、 D4以随机的比例系数合成。随机的比例系数都满足和为一，非负两个条件。为了更加贴近真实的高光谱数据，添加信噪比为30 dB的高斯白噪声,这样仿真的高光谱数据满足各个像元的地物类型和数目均不同的条件。各个地物端元的丰度图如图5所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 合成数据(第3波段）

Fig.4 Synthetic data(the third band)

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 4类端元的丰度图

Fig.5 Abundance maps of four endmenbers

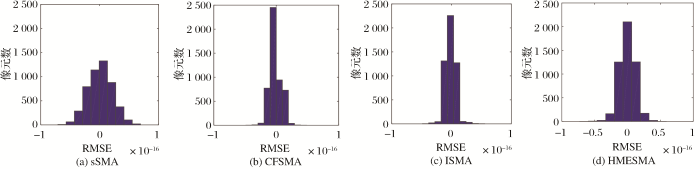
表1分别是sSMA、CFSMA、ISMA、HMESMA算法求得的丰度和真实丰度的RMSE对比。从表１可以看出CFSMA、ISMA、HMESMA算法明显优于sSMA，说明它们在克服类内光谱变化上均起到了积极作用，也说明多端元光谱混合分析模型更加合理，且CFSMA的解混丰度误差最低，CFSMA和ISMA算法的解混丰度误差明显低于HMESMA算法。图6给出了各种算法的丰度误差直方图，图6(a)为sSMA算法采用的是固定的端元集解混求得的丰度误差结果，其中丰度误差聚集在0值附近接近1 500个像元，图6(b) CFSMA算法解混求得的丰度误差结果，其中丰都误差聚集在0值附近接近2 500个像元，图6(c)和6(d) ISMA和HMESMA算法解混求得的丰度误差结果，其中丰都误差聚集在0值附近为2 000个像元左右，从4种算法的直方图可以看出CFSMA算法的解混丰度误差最低，sSMA算法的解混丰度误差最高。图7显示了4种算法的解混丰度图，自左向右分别代表sSMA、CFSMA、ISMA、HMESMA算法的解混丰度图，至上向下分别表示明矾石,橄榄石,绿泥石,白云母4种地物, 与图5的4类地物的真实丰度图对比，再一次验证CFSMA算法的优越性，CFSMA算法解混分量图不该含有该类别端元的区域丰度基本为零，而传统sSMA反演丰度值有很多应该为零的区域却不为零。

表1 解混丰度误差对比

Table 1 Unmixing abundance error contrast

算法	明矾石	橄榄石	绿泥石	白云母	平均
sSMA	0.12	0.06	0.14	0.10	0.10
CFSMA	0.03	0.03	0.03	0.03	0.03
ISMA	0.03	0.04	0.04	0.03	0.04
HMESMA	0.04	0.05	0.04	0.03	0.04

新窗口打开| 下载CSV

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 丰度误差直方图

Fig.6 Abundance error histograms of different algorithms

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 4类端元丰度图对比

至上向下分别表示明矾石、橄榄石、绿泥石和白云母

Fig.7 Abundance maps of four endmenbers

仿真实验2：将高斯噪声附加在实验1的合成图像中，得到10到60之间的6个逐渐增大的信噪比的合成图像，实验比较在不同信噪比的情况下实现解混的效果。图8分别给出了在信噪比从10到60变化的过程中3种算法解混下4种地物的平均丰度误差值（RMSE）变化,由图8可知随着高斯噪声的信噪比增加，ISMA、sSMA、HMESMA解混平均丰度误差在信噪比为30之前呈快速下降趋势，而sSMA呈缓慢下降趋势，解混平均丰度误差信噪比为30以后呈稳定趋势。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 不同信噪比下RMSE值

Fig.8 RMSE values for different SNRs

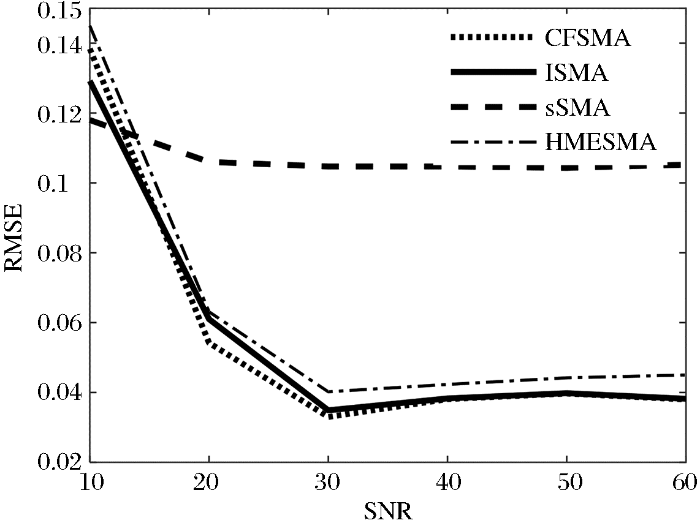
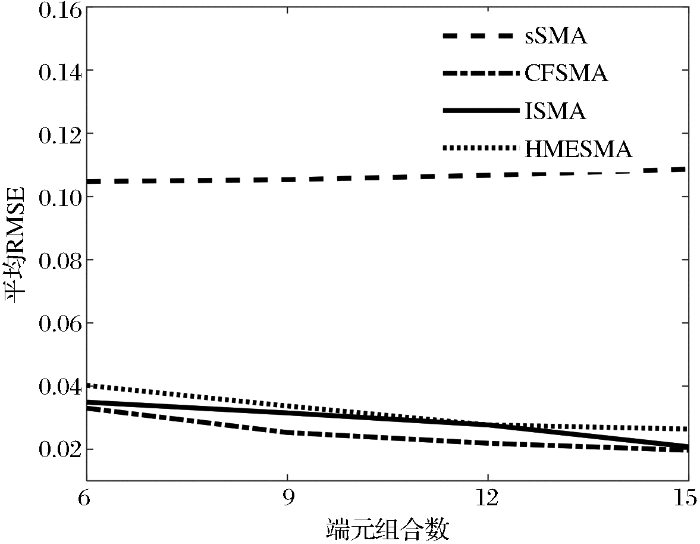
仿真实验3：实验中采用实验1使用的合成数据，且图像大小固定为50×100，信噪比固定为30 dB，端元组合为6到15依次变化，4种算法解混RMSE值变化如表2所示,可以看出sSMA算法解混丰度误差最高，而CFSMA算法解混误差始终最低,ISMA算法解混误差始终低于HMESMA。图9为4种解混算法平均丰都误差的曲线图，从图9可以更加直观地看出随着元组合数目的增加，sSMA算法解混丰度误差几乎保持不变，而CFSMA、ISMA、HMESMA算法的解混丰度误差随着端元组合的增加，丰度误差呈下降趋势，而CFSMA算法解混误差曲线始终位于其他解混算法曲线下面，而sSMA算法解混误差曲线始终在最上方。表3为4种解混算法在不同端元组合数目所消耗的时间比较，根据表3结果可知，sSMA、CFSMA、HMESMA算法随着端元组合数目的增加,解混时间保持不变，其中HMESMA算法消耗的时间最短，CFSMA算法消耗的时间比HMESMA算法多1 s左右，而IMSA的解混时间消耗最长，且随着端元组合数目的增加，解混时间有缓慢上涨的趋势。

表2 4种解混算法与端元组合数目的丰度误差比较

Table 2 Compare with unmixing abundance error between four unmixing algorithm and combinations of endmembers

端元组合数	算法	明矾石	橄榄石	绿泥石	白云母	均值
6	sSMA	0.12	0.06	0.14	0.10	0.10
	CFSMA	0.03	0.03	0.03	0.03	0.03
	ISMA	0.03	0.04	0.04	0.03	0.04
	HMESMA	0.04	0.05	0.04	0.03	0.04
9	sSMA	0.12	0.07	0.12	0.10	0.10
	CFSMA	0.02	0.03	0.03	0.02	0.03
	ISMA	0.02	0.04	0.04	0.02	0.03
	HMESMA	0.03	0.04	0.04	0.02	0.03
12	sSMA	0.10	0.11	0.10	0.11	0.11
	CFSMA	0.01	0.02	0.03	0.02	0.02
	ISMA	0.02	0.03	0.03	0.02	0.03
	HMESMA	0.02	0.04	0.04	0.02	0.03
15	sSMA	0.11	0.10	0.13	0.10	0.11
	CFSMA	0.01	0.03	0.02	0.01	0.02
	ISMA	0.02	0.02	0.03	0.01	0.02
	HMESMA	0.02	0.03	0.03	0.02	0.03

新窗口打开| 下载CSV

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 平均丰度误差曲线图

Fig.9 Average fractional abundance error

表3 4种解混算法与端元组合数目的时间比较（单位：s）

Table 3 Compare with time between four unmixing algorithm and combinations of endmembers(Unit:s)

端元组合数目	6	9	12	15
sSMA	0.34	0.36	0.35	0.35
CFSMA	4.72	4.73	4.73	4.73
ISMA	27.36	31.13	36.18	42.25
HMESMA	3.02	3.12	3.12	3.13

新窗口打开| 下载CSV

4.2　真实数据实验

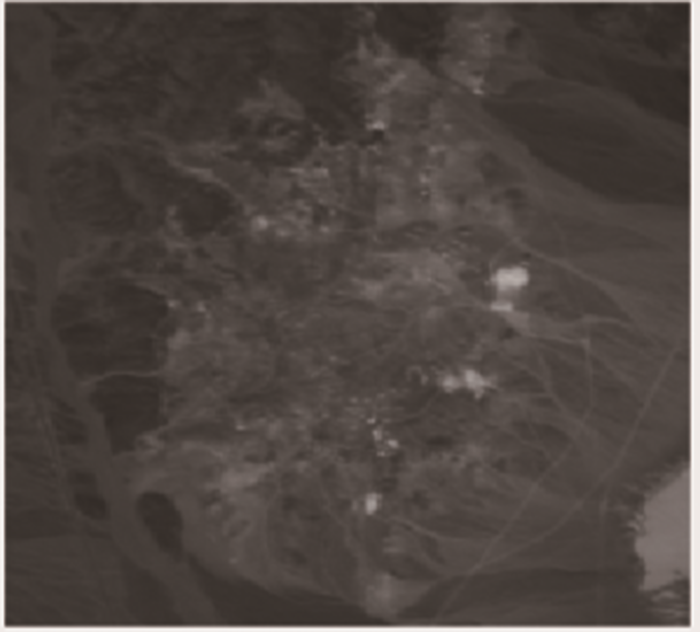
实验采用的是Cuprite 矿物数据如图10所示，像由 AVIRIS 传感器获得，实验所用数据大小为 250×191 像元，光谱范围为0.369~2.480 μm，共224波段，去除因水汽吸收和传感器噪声等低信噪比波段(1~2、104~113、148~167、221~224)，实验用的数据共 188 波段。参考[21]从Cuprite 矿物数据中选取了39条端元，分别为：Alunite（6条类内光谱）、Kaolinite（8条类内光谱）、Andradite（5条类内光谱）、Nontronite（5条类内光谱）、Muscovite（2条类内光谱）、Dumortierite（1条类内光谱）、Montmorillonite（10条类内光谱）、Buddingtonite（2条类内光谱）。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 Cuprite矿物数据(第20波段)

Fig.10 Cuprite subscene (the 20th Bands)

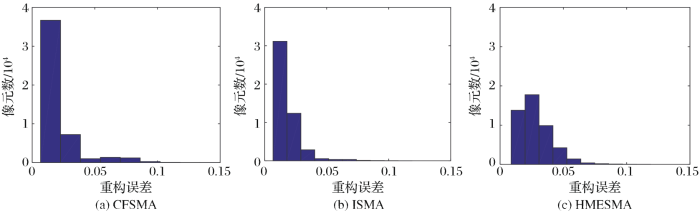
图11是3种算法解丰度图对比，其中灰度越亮代表该类别在所对应的混合像元中的丰度值越大，反之亦然，其中HMESMA算法解混的地物丰度图比较模糊，不能有效区分不同地物，由于HMESMA解混算法仅仅考虑到光谱角距离近似判断最优端元组合，解混效果不如ISMA和CFSMA算法解混效果，由于地物分布比较复杂，丰度图从视觉上无法直接给出更好的判断，为了更好地分析实验结果，使用重构误差评价解混效果，重构误差越低，解混效果越好，反之亦然，图12给出了3种解混算法的重构误差直方图,由图12可知，CFSMA重构误差在0.01占约38 000个像元，ISMA重构误差在0.01占约33 000个像元，HMESMA重构误差在0.01占约20 000个像元。表4为3种算法解混所消耗的时间对比，由表4可知，ISMA用时较长，时间复杂度比较高，不适合实际的应用，HMESMA算法消耗的时间最短，但是解混重构误差最大，而CFSMA算法解混重构误差最小，且消耗的时间只比HMESMA算法相接近，因此最适合实际的应用。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 Cuprite 8种端元丰度图

(左边为CFSMA解混丰度图，中间为ISMA解混丰度图，右边为HMESMA)

Fig.11 Abundance maps of eight endmenbers

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 3种算法重构误差直方图

Fig.12 Reconstruction error histograms of three algorithms

表4 3种解混算法消耗时间对比

Table 4 Compare with time of three unmixing algorithm

解混算法	CFSMA	ISMA	HMESMA
时间/s	148.16	5100．35	112.61

新窗口打开| 下载CSV

5 结语

为了有效降低计算复杂度的同时提高光谱解混精度，提出了一种新的多端元光谱混合分析方法。利用所有端元做一次全约束光谱混合分析确定每个像元的初始端元集，在此基础上基于ISMA 的思想完成每个像元的精细光谱分析。实验结果表明，本文提出的CFSMA算法可以克服类间光谱变化，CFSMA解混算法所消耗的时间远远小于ISMA，且CFSMA算法解混误差低于ISMA算法，当端元组合数增加的时候，解混的精度不会降低，如何自适应地选择阈值是下一步工作的重点。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Tong

Qingxi

, Zhang

Bing

, Zheng

Lanfen

Hyperspectral Remote Sensing

[M]. Beijing: Higher Education Press, 2006.