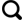遥感技术与应用, 2020, 35(3): 615-622 doi: 10.11873/j.issn.1004-0323.2020.3.0615

模型与反演

基于3种机器学习法的太阳辐射模拟研究

李净,, 温松楠,

西北师范大学 地理与环境科学学院，甘肃 兰州 730070

Simulation of Solar Radiation based on Three Machine Learning Methods

Li Jing,, Wen Songnan,

The College of Geographical and Environmental Science, Northwest Normal University, Lanzhou 730070, China

通讯作者: 温松楠(1995-)，女，甘肃天水人，硕士研究生，主要从事定量遥感与辐射模拟研究。E-mail:18893111471@163.com

收稿日期: 2019-06-04   修回日期: 2020-05-07   网络出版日期: 2020-07-03

基金资助: 国家自然科学基金项目.  41261016.  41761083.  41561016
西北师范大学青年教师科研能力提升计划项目.  NWNU-LKQN-14-4

Received: 2019-06-04   Revised: 2020-05-07   Online: 2020-07-03

作者简介 About authors

李净(1978-)，女，甘肃会宁人，副教授，硕士生导师，主要从事定量遥感研究E-mail:li_jinger@163.com , E-mail：li_jinger@163.com

摘要

定量模拟太阳辐射对认识黄土高原区气候变化至关重要，现有研究表明机器学习可以很好地模拟太阳辐射，但不同的机器学习法在不同区域模拟精度不同，为了实现黄土高原区太阳辐射数据的最优模拟，从而为农作物模型、水文模型以及气候变化模型提供精度更高的太阳辐射数据。基于随机森林（RF，Random Forest）、人工神经网络（ANN,Artificial Neural Network）和支持向量机（SVM,Support Vector Machine）3种机器学习法来模拟黄土高原地区的太阳辐射并对这3种算法进行比较研究，选取了2003~2009年14个辐射站点和2010~2016年10个辐射站点的实测数据和对应参数气压、云量、云光学厚度、臭氧、可降水水汽以及DEM、坡度、坡向作为模型的训练数据，随机选取2010~2016年4个辐射站点的太阳辐射实测数据对模拟结果进行验证。验证结果表明：RF模型在黄土高原及周边地区的模拟效果最优，平均偏差(MBE)为-0.17 MJ·m-2，均方根误差(RMSE)为1.48 MJ·m-2，拟合优度达到0.96。研究结果表明:RF模型与气象数据及遥感数据结合能够有效解决黄土高原无辐射观测区的太阳辐射模拟问题，对区域太阳辐射的研究具有重要意义。

关键词： 太阳辐射 ; 随机森林(RF) ; 人工神经网络（ANN) ; 支持向量机（SVM) ; 遥感

Abstract

Quantitative simulation of solar radiation is essential for understanding climate change 0n the Loess Plateau, Many machine learning methods were developed to estimate solar radiation well, but different machine learning methods have different simulation accuracy in different regions, In order to achieve optimal simulation of solar radiation on the Loess Plateau, this provides more higher precision solar radiation data for crop models, hydrological models, and climate change models. In this study, three machine learning methods, including Random Forest (RF), Artificial Neural Network (ANN) and Support Vector Machine (SVM), were applied to estimate solar radiation on the Loess Plateau, three machine learning methods were trained using ground measurements at fourteen radiation sites from 2003 to 2009 and ten radiation sites from 2010 to 2016 and corresponding parameter pressure, cloud fraction, cloud optical thickness, ozone, precipitation water vapor and DEM, slope, and aspect to train the three model, The solar radiation estimates based on three machine learning methods were evaluated using ground measurements at four radiation sites from 2010 to 2016. The validation results show that the RF model has the best simulation effect on the Loess Plateau and surrounding areas. The average deviation is -0.17 MJ·m-2, the root mean square error is 1.48 MJ·m-2, and has a good fit of 0.96. The results show that combined RF model and meteorological data and remote sensing data can effectively solve the problem about solar radiation simulation on the non-radiation observation area of the Loess Plateau, which is of great significance to the research of regional solar radiation.

Keywords： Solar radiation ; Random Forest(RF) ; Artificial Neural Network(ANN) ; Support Vector Machine(SVM) ; Remote sensing

PDF (3463KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

李净, 温松楠. 基于3种机器学习法的太阳辐射模拟研究. 遥感技术与应用[J], 2020, 35(3): 615-622 doi:10.11873/j.issn.1004-0323.2020.3.0615

Li Jing, Wen Songnan. Simulation of Solar Radiation based on Three Machine Learning Methods. Remote Sensing Technology and Application[J], 2020, 35(3): 615-622 doi:10.11873/j.issn.1004-0323.2020.3.0615

1 引 言

太阳辐射是地气系统最重要的能量来源和驱动力[1]，其变化对大气热力状况、生物生长以及人类活动等具有显著的影响[2]，太阳辐射数据也是农作物模型、水文模型及气候变化模型等的重要参数[3,4]。获取精确的太阳辐射数据是研究太阳辐射时空变化分布的重要前提，由于太阳辐射站点分布稀疏，很难通过稀少的站点插值得到空间连续分布的太阳辐射[5]，但气象站点分布相对比较密集再加上遥感数据可以提供部分模拟太阳辐射的大气参数[6]，因此，利用遥感数据结合气象数据模拟太阳辐射对区域太阳辐射研究具有重要意义。

目前太阳辐射模拟主要有理论参数模型[7,8]、经验模型[9,10]、人工智能模型[11,12,13]和卫星遥感反演模型[14,15]四类。理论参数模型计算公式复杂、经验模型只适合局部范围，卫星反演数据虽然可以提供大范围连续的空间分布信息，但卫星产品精度的提高需要地面观测资料的修正。很多研究表明机器学习算法模拟的太阳辐射精度较高，Sun等[16]利用空气污染指数基于随机森林模型估算日太阳辐射，并与经验模型做比较，结果表明随机森林模型模拟效果更优。Benali等[17]用智能持久性，人工神经网络和随机森林3种方法来估算了法国的太阳辐射，比较发现随机森林模型模拟精度更高。梁益同等[18]利用FY-2C气象卫星资料，利用神经网络方法估算了华中三省（湖北、湖南和河南）逐时的太阳辐射，并与统计方法做比较，结果表明人工神经网络方法模拟效果更优。Deo等[19]用MODIS地表温度数据基于人工神经网络模型估算了长时间连续的太阳辐射，并与其他回归模型模拟结果进行比较，结果表明ANN模型模拟精度较好。Fallahi等[20]利用人工神经网络模型和多元线性回归模型估算了伊朗库尔德斯坦省的月平均太阳辐射，结果表明，与多元线性回归模型相比，ANN模型模拟准确性更高。Yao等[21]基于支持向量机模型，以空气质量指数为输入参数，估算了全球太阳辐射，与其他模型相比，支持向量机模型与空气质量指数结合估算太阳辐射具有更高精度。由此可见，基于人工神经网络、随机森林、支持向量机3种机器学习法估算太阳辐射有很大的优势。同时有研究表明气象数据与遥感数据结合模拟太阳辐射精度更高，李净等[22]利用神经网络模型模拟太阳辐射，验证结果表明，将MODIS大气产品和常规气象站点数据结合作为输入参数之后，各项误差指标均小于仅用常规气象站点数据模拟的太阳辐射结果。

太阳辐射数据是农作物模型、水文模型以及气候变化模型等的重要参数，不同的机器学习法结合遥感和气象数据在不同区域模拟太阳辐射效果不同，为了解决黄土高原区辐射站点稀少造成的太阳辐射模拟精度低的问题，实现黄土高原区太阳辐射数据的最优模拟，基于随机森林（RF，Random Forest）、人工神经网络（ANN,Artificial Neural Network）和支持向量机（SVM,Support Vector Machine）3种机器学习法，结合气象数据和遥感数据来模拟黄土高原区的太阳辐射，并对这3种算法进行比较研究。

2 研究区及数据

2.1　研究区概况

黄土高原区位于中国中部偏北部，包含青海、甘肃、宁夏、陕西、山西、河南、内蒙古部分地区。选取黄土高原及周边地区作为研究区（如图1）对太阳辐射进行模拟研究，该区域位于99°21′~115°14′E，32°13′~41°15′N，面积约为130×104 km2。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   黄土高原地区辐射站点图

Fig.1   Radiation sites in Loess Plateau


2.2　数 据

选取的遥感数据为MODIS大气三级标准数据产品MOD08-D3（V005），来源于NASA官网，提取了MOD08-D3（V005）产品2003~2016年每月的云量（CF）、云光学厚度（COT）、臭氧（O3）、可降水水汽（PWV）的月均值数据，空间分辨率为1°×1°。

气象数据由中国气象数据网（http://data.cma.cn/）提供，考虑到数据完整性及时间序列一致性，选取了97个气象站点和14个辐射站点的数据进行研究，包括2003~2016年的月平均气压和太阳辐射月均值数据，辐射站点数据主要用于模型的训练和验证，其中，兰州2005年迁到了榆中。

3 研究方法

3.1　随机森林

随机森林是2001年由Breiman开发的一种基于套袋的方法，使用了回归树的集合机器学习技术[23]。通过Python中的Pandas准备数据框数据，导入Sklearn工具包，在Sklearn模块库中，与随机森林算法相关的函数都位于集成算法模块Ensemble中，利用一系列运算代码实现随机森林模型预测太阳辐射。

随机森林算法的具体步骤为：首先从N个总样本中重复取样n次，得到n个样本集作为一组训练集，未被抽取的部分组成袋外数据进行类别预测，并评估其误差；对每个决策树节点随机选取m个变量（m小于M，M为自变量个数），根据m个变量计算最佳分割方式；每棵树最大限度生长，不做裁剪；由生成的多棵决策树组成随机森林，用随机森林做回归分析，以每棵决策树输出结果的平均值作为预测值[24,25]，如下式所示：

Y(xi)=1n∑1nTn(xi)n=1,2,3,...,n

其中：Tn为每棵决策树，n为决策树的个数。

3.2　BP神经网络

目前人工神经网络模型已经有BP、RBF、MLP、GRNN等几十种结构，其自学能力较强[26,27]。本文利用LM（Levenberg-Marquardt）算法优化后的BP神经网络模型来模拟太阳辐射，LM算法又称阻尼最小二乘法，是梯度下降法与高斯—牛顿法的结合，由输入层、隐含层和输出层组成，对于一个输入样本，经过权值、阈值、激活函数运算后，得到一个输出点，然后让它与期望的样本进行比较，若有偏差，则从输出开始反向传播该偏差，进行权值、阈值调整，使网络输出逐渐与希望输出一致。LM-BP神经网络的训练函数采用trainlm，其学习规则为：

x(k+1)=x(k)-[JTJ=μI]-1JTe

其中：e为误差向量；J为网络误差对权值导数的Jacobian矩阵；I为单位矩阵；u为一标量，其值决定了算法是根据牛顿法还是梯度法来实现。当系数u为0时，上式即为牛顿法；当系数u的值很大时，上式变为步长较小的梯度下降法。

3.3　支持向量机

Vapnik等[28,29]提出的支持向量机（SVM）经过训练可以解决凸优化问题，以置信范围值最小化作为优化目标，其目标函数为：

min12pwp2+C∑i(ξi+ξi*)
yi-(wTxi+b)<ε+ξi(wTxi+b)+yi<ε+ξiξi,ξi*≥0

其中：ξi和ξi*是松弛系数，C是惩罚系数。为了解决上述优化问题，将非负拉格朗日引入乘数来消除约束项，此外，SVM中的核函数能够将非线性数据映射到高维空间，本文通过python尝试不同的核函数模拟效果，最终选取了径向基（RBF）核函数，公式如下：

K(xi,xj)=exp(-γpxi-xjp2)

其中：exp为以自然常数e为底的指数函数，pxi-xjp代表xii到xj的欧氏距离，γ是自定义参数。

4 结果分析

4.1　模型构建及性能比较

影响太阳辐射的因素很多，气象站点只能获取到部分影响因素的数据，因此本文还选取了MODIS的云量、云光学厚度、臭氧、可降水水汽遥感数据以及DEM、坡度、坡向数据，由于RF、ANN、SVM等机器学习算法的物理机理是一个“黑箱”，随着变量增加，黑箱建模的程度也更复杂，因此需要通过科学的分析来选取模拟的输入参数。本文分析了各站点平均气压、平均水汽压、平均相对湿度、风速、日照时数、MODIS产品云量、云光学厚度、臭氧、可降水水汽与太阳辐射实测值的相关性，剔除了与太阳辐射相关系数较小的变量，选择了平均气压、MODIS产品云量、云光学厚度、臭氧、可降水水汽以及地理参数DEM、坡度、坡向共8个变量作为模型的输入参数。

以Python2.7和Mattalab2014为计算平台，将黄土高原及周边地区2003~2009年14个辐射站点和2010~2016年10个辐射站点的实测数据和对应站点提取的气压、云量、云光学厚度、臭氧、可降水水汽以及DEM、坡度、坡向作为模型的训练数据，首先分别对3种模型进行训练，各个模型输入的最佳参数及模型误差指标如表1所示，采用相关系数（R）、平均偏差（MBE）、均方根误差（RMSE）对模拟结果进行精度评价[30]。由表1可知，RF模型训练和验证的拟合优度都最好，SVM模型训练的平均偏差MBE最小，RF模型训练的均方根误差RMSE最小，模型验证时，RF模型的平均偏差MBE和均方根误差RMSE均最小，相关系数最大，由此可知，RF模型更有优势。

表1   模型误差

Table1  Parameter、training and verification error of Model

训练误差验证误差
模型参数MBE/MJ·m-2RMSE/MJ·m-2RMBE/MJ·m-2RMSE/MJ·m-2R
RF最大特征数8、最大深度100.252.430.92-0.171.480.96
SVM核函数为RBF、gamma为0.02、C为100000.162.660.841.552.630.92
ANN训练函数为trainlm、神经网络结构为8-20-1-1.344.270.73-1.144.010.75

新窗口打开| 下载CSV


4.2　精度比较

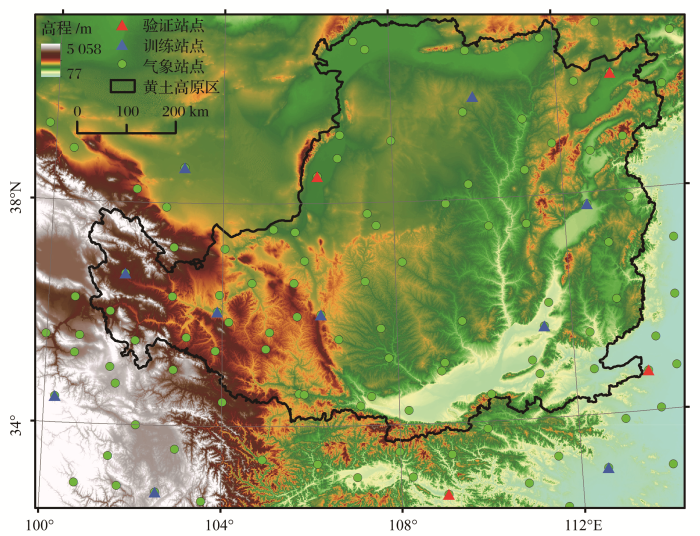
利用2010~2016年大同、银川、郑州、安康4个辐射站点的太阳辐射实测数据对RF、ANN以及SVM3个模型的模拟结果进行验证，3种模型模拟结果与实测值对比（如图2），RF模型在4个辐射站点的模拟值和实测值最接近，平均偏差控制在-0.5~0.3 MJ·m-2内，ANN模型在银川站的模拟值有轻幅高估，在大同、郑州、安康3个辐射站的模拟值有低估，尤其大同站点低估最明显，SVM模型在郑州站的模拟值与实测值较接近，平均偏差为0.02 MJ·m-2，在大同、银川、安康站点模拟值有明显高估，高估幅度在0.2~3.5 MJ·m-2之间波动。SVM模拟结果虽在大同、银川、安康站点存在3.5 MJ·m-2幅度以内的高估，但SVM的模拟值与实测值在2010~2016年每月的变化趋势基本一致，银川和郑州站点的拟合优度最好，达到0.97。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   太阳辐射月均值模拟值与实测值对比

Fig.2   Comparision between observed and measured value of monthly average solar radiation


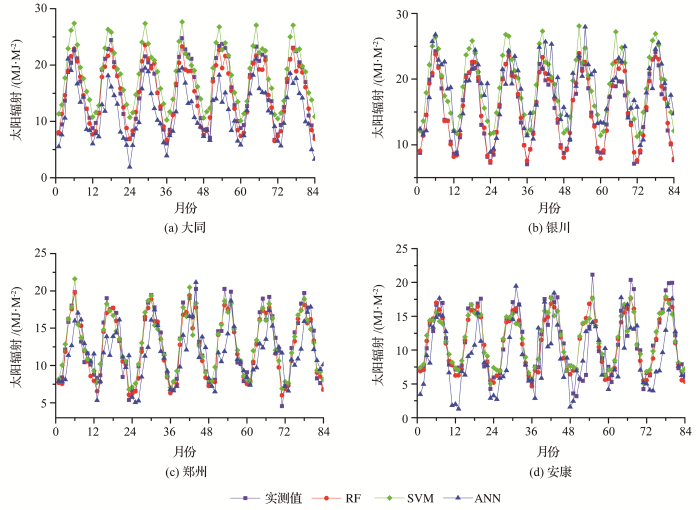
采用相关系数（R）、平均偏差（MBE）、均方根误差（RMSE）对2010~2016年每月的太阳辐射模拟结果进行精度评价，评价结果如图3所示。RF模型在4个辐射站点模拟值的误差均较小，平均偏差MBE控制在-1.6~2.5 MJ·m-2之间，均方根误差RMSE在2014年的安康站点最大，达到4.40 MJ·m-2，其余各年份不同站点的均方根误差RMSE均控制在2 MJ·m-2范围内，总体上，RF模型的平均偏差、均方根误差指标值都较小，表明模拟值偏离实测值程度较小，RF模拟值与实测值的相关系数除安康站点（2014年为0.68）外，都大于0.93，大多数达到0.99，表明RF模型的模拟值与实测值相关程度高。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   模拟验证误差

Fig.3   Verification error of simulation


SVM模型在郑州、安康站点模拟值的误差较小，平均偏差MBE在-0.6~2.5 MJ·m-2之间变化，，均方根误差RMSE控制在5.3 MJ·m-2以内，而在大同、银川站点的误差较大，平均偏差MBE在1.5~4.5 MJ·m-2之间变化，表明模拟值有明显高估，大同、银川站点的均方根误差RMSE在0~4.5 MJ·m-2之间波动，SVM模拟值与实测值的相关性较好，除安康站点外（2014年，0.70），都大于0.93，说明2010~2016年模拟值和实测值的变化趋势大体一致。

ANN模型在大同、郑州、安康3个站点的平均偏差MBE除安康站点外（2014年为0.30）均小于0，说明模拟值有低估，低估幅度控制在5.5 MJ·m-2以内，均方根误差RMSE均在1~6 MJ·m-2之间波动，银川站点平均偏差为1~4 MJ·m-2之间波动，说明模拟值有高估，ANN模拟值与实测值的相关系数均在0.6~0.9之间，大同站点模拟值和实测值的相关系数均达到0.9以上，说明大同站模拟值和实测值的相关性较高。

通过比较RF、SVM、ANN 3种模型的误差指标以及相关系数得出RF模型的各个误差指标均较小，相关系数大，说明RF模型模拟效果最优，SVM次之，ANN模拟精度最低。

5 结 语

5.1　讨 论

本文利用气象站的气压和MODIS遥感产品云量、云光学厚度、臭氧、可降水水汽以及DEM、坡度、坡向构建了RF、SVM、ANN 3种模型，首先将3种模型的模拟结果与实测值对比发现，基于RF模型估算的太阳辐射平均值（13.67 MJ·m-2）与辐射站点观测数据（13.84 MJ·m-2）接近，但估算的太阳辐射变化范围（4.65~23.94 MJ·m-2）比观测数据（3.18~24.75 MJ·m-2）略微偏小，轻幅高估太阳辐射的低值、低估太阳辐射的高值。SVM模型估算的太阳辐射平均值（15.40 MJ·m-2）有高估，估算的太阳辐射变化范围（5.03~28.09 MJ·m-2）比观测数据（3.18~24.75 MJ·m-2）偏大，对太阳辐射的低值和高值都有高估。ANN模型估算的太阳辐射平均值（12.71 MJ·m-2）有低估，估算的太阳辐射变化范围（1.29~27.93 MJ·m-2）比观测数据（3.18~24.75 MJ·m-2）明显偏大，低估太阳辐射低值、高估太阳辐射的高值。也有研究发现类似的结果，Meenal等[31]基于SVM、ANN以及经验模型模拟了印度不同城市的太阳辐射，结果表明SVM模型对太阳辐射有轻幅高估。李净等[32]研究表明ANN模型对太阳辐射的模拟有低估，平均偏离误差在控制在-1~1 MJ·m-2之间。

然后利用地面辐射站点观测的太阳辐射实测数据对3种模型模拟结果进行验证，并对3种模型的模拟精度进行比较。结果表明，RF模型在黄土高原及周边地区对太阳辐射的模拟精度（RMSE=1.48 MJ·m-2，MBE=-0.17 MJ·m-2，R=0.96）明显优于SVM（RMSE=2.63 MJ·m-2，MBE=1.55 MJ·m-2，R=0.92）和ANN（RMSE=4.01 MJ·m-2，MBE=-1.14 MJ·m-2，R=0.75）模型，SVM模型次之，ANN模型模拟精度最低。Benali等[17]用智能持久性（SP），人工神经网络（ANN）和随机森林（RF）3种方法来估算了法国的太阳辐射，比较发现RF模型模拟精度更高。Wei等[33]基于梯度增强回归（GBRT）、随机森林（RF）、多元自适应回归样条（MARS）和人工神经网络（ANN）模拟了中国晴空和多云条件下的太阳辐射，分别在日尺度和月尺度验证了模拟结果，验证结果表明，无论在晴空还是多云条件下，基于RF模型的日、月尺度太阳辐射的模拟精度均比ANN模型好。Meenal等[31]基于SVM、ANN以及经验模型模拟了印度不同城市的太阳辐射，结果表明，SVM模型模拟精度比ANN模型高，这与本文的研究结果相似。以上研究进一步表明RF模型的可靠性。

5.2　结 论

本文基于RF、SVM、ANN 3种模型模拟了黄土高原及周边地区太阳辐射月均值，比较分析了3种模型的模拟结果及精度。通过本文的研究得出以下主要结论：

（1）本文通过比较RF、ANN、SVM 3种模型的训练结果得出RF模型训练的平均偏差MBE最小，为0.16 MJ·m-2，RF模型训练的均方根误差RMSE最小，为2.43 MJ·m-2，RF模型训练的拟合优度最好，达到0.92，由此可知，RF模型更有优势。

（2）本文利用太阳辐射实测数据对RF、ANN、SVM 3种模型的模拟结果进行验证，结果表明RF模型的各个误差指标均较小，平均偏差MBE大部分在-1~2 MJ·m-2之间波动，均方根误差RMSE均控制在2 MJ·m-2范围内，RF模拟值与实测值的相关系数大多数达到0.99，表明RF模型的模拟值与实测值之间的拟合程度明显高于其他两个模型，模型精度最高。总体上，RF模型模拟黄土高原及周边地区的太阳辐射效果最优，SVM次之，ANN模拟精度最低。

（3）RF模型的优越性体现在同等运算率下的高预测精度，对非线性数据有很好的拟合效果，减少了均方根误差，提高了模型的预估精度，RF模型与气象数据及遥感数据结合模拟太阳辐射月均值是一种精度较高且可靠的模拟方法，可以有效解决黄土高原区辐射站点稀少造成的太阳辐射模拟精度低的问题。

参考文献

Sun H, Zhao N, Zeng X, et al.

Study of Solar Radiation Prediction and Modeling of Relationships between Solar Radiation and Meteorological Variables

[J]. Energy Conversion and Management, 2015, 105: 880-890. doi:10.1016/j.enconman.2015.08.045.

[本文引用: 1]

Chen J L, Li G S, Wu S J.

Assessing the Potential of Support Vector Machine for Estimating Daily Solar Radiation Using Sunshine Duration

[J]. Energy Convers Manage， 2013，75:311-318.

[本文引用: 1]

Shi Guoping, Qiu Xinfa, Zeng Yan.

Distributed Simulation of Three Solar Radiation Starting Data in China

[J]. Geographical Science, 2013, 33(4): 385-392.

[本文引用: 1]

施国萍, 邱新法, 曾燕.

中国三种太阳辐射起始数据分布式模拟

[J]. 地理科学, 2013, 33(4): 385-392.

[本文引用: 1]

Li Weiwei, Letu Husi, Chen Hongbin.

Calculation of Surface Solar Radiation Under Different Cloud Conditions Using MODIS Data

[J]. Remote Sensing Technology and Application, 2017，32(4): 643-650.

[本文引用: 1]

黎微微, 胡斯勒图， 陈洪滨.

利用 MODIS 资料计算不同云天条件下的地表太阳辐射

[J]. 遥感技术与应用, 2017,32(4): 643-650.

[本文引用: 1]

Journée M, Bertrand C.

Improving the Spatio-temporal Distribution of Surface Solar Radiation Data by Merging Ground and Satellite Measurements

[J]. Remote Sensing of Environment, 2010, 114(11): 2692-2704.

[本文引用: 1]

Zhang T, Stackhouse Jr P W, Gupta S K, et al.

The Validation of the GEWEX SRB Surface Shortwave Flux Data Products Using BSRN Measurements: A Systematic Quality Control, Production and Application Approach

[J]. Journal of Quantitative Spectroscopy and Radiative Transfer, 2013, 122: 127-140.

[本文引用: 1]

Huang G, Liang S, Lu N, et al.

Toward a Broadband Parameterization Scheme for Estimating Surface Solar Irradiance: Development and Preliminary Results on MODIS Products

[J]. Journal of Geophysical Research: Atmospheres, 2018, 123(21): 12180-12193.

[本文引用: 1]

Gueymard C A, Myers D R.

Evaluation of Conventional and High-performance Routine Solar Radiation Measurements for Improved Solar Resource, Climatological Trends, and Radiative Modeling

[J]. Solar Energy, 2009, 83(2): 171-185.

[本文引用: 1]

Angstrom A.

Solar and Terrestrial Radiation. Report to the International Commission for Solar Research on Actinometric Investigations of Solar and Atmospheric Radiation

[J]. Quarterly Journal of the Royal Meteorological Society, 1924, 50(210): 121-126.

[本文引用: 1]

Li R, Zhao L, Wu T, et al.

Temporal and Spatial Variations of Global Solar Radiation over the Qinghai-Tibetan Plateau during the Past 40 Years

[J]. Theoretical and Applied Climatology, 2013, 113(3-4): 573-583.

[本文引用: 1]

Mummadisetty B C, Puri A, Sharifahmadian E, et al.

A hybrid Method for Compression of Solar Radiation Data Using Neural Networks

[J]. International Journal of Communications, Network and System Sciences, 2015, 8(6): 217. doi:10.4236/ijcns.2015.86022.

[本文引用: 1]

Belaid S, Mellit A.

Prediction of Daily and Mean Monthly Global Solar Radiation Using Support Vector Machine in an Arid Climate

[J]. Energy Conversion and Management, 2016, 118: 105-118.

[本文引用: 1]

Chen R, Ersi K, Yang J, et al.

Validation of Five Global Radiation Models with Measured Daily Data in China

[J]. Energy Conversion and Management, 2004, 45(11-12): 1759-1769.

[本文引用: 1]

Peng Z, Letu H, Wang T, et al.

Estimation of Shortwave Solar Radiation Using the Artificial Neural Network from Himawari-8 Satellite Imagery over China

[J]. Journal of Quantitative Spectroscopy and Radiative Transfer, 2020, 240: 106672.

[本文引用: 1]

Zhu X, Qiu X, Zeng Y, et al.

A Remote Sensing Model to Estimate Sunshine Duration in the Ningxia Hui Autonomous Region, China

[J]. Journal of Meteorological Research, 2015, 29(1): 144-154.

[本文引用: 1]

Sun H, Gui D, Yan B, et al.

Assessing the Potential of Random Forest Method for Estimating Solar Radiation Using Air Pollution Index

[J]. Energy Conversion and Management, 2016, 119: 121-129.

[本文引用: 1]

Benali L, Notton G, Fouilloy A, et al.

Solar Radiation Forecasting Using Artificial Neural Network and Random Forest Methods: Application to Normal Beam, Horizontal Diffuse and Global Components

[J]. Renewable Energy, 2019, 132: 871-884.

[本文引用: 2]

Liang Yitong, Liu Kequn, Xia Zhihong. Estimation of Solar Radiation Using FY-2

C Satellite Data

[J]. Meteorological Science and Technology, 2009, 37(2): 234-238.

[本文引用: 1]

梁益同, 刘可群, 夏智宏.

利用FY-2C卫星资料估算太阳辐射研究

[J]. 气象科技, 2009, 37(2):234-238.

[本文引用: 1]

Deo R C, Şahin M.

Forecasting Long-term Global Solar Radiation with an ANN Algorithm Coupled with Satellite-derived (MODIS) Land Surface Temperature (LST) for Regional Locations in Queensland

[J]. Renewable and Sustainable Energy Reviews, 2017, 72: 828-848.

[本文引用: 1]

Fallahi S, Amanollahi J, Tzanis C G, et al.

Estimating Solar Radiation Using NOAA/AVHRR and Ground Measurement Data

[J]. Atmospheric Research, 2018, 199: 93-102.

[本文引用: 1]

Yao W, Zhang C, Hao H, et al.

A Support Vector Machine Approach to Estimate Global Solar Radiation with the Influence of fog and Haze

[J]. Renewable Energy, 2018, 128: 155-162.

[本文引用: 1]

Li Jing, Wang Dan, Feng Wei.

Simulation of Solar Radiation based on MODIS Remote Sensing Products and Neural Networks

[J]. Geographical Science, 2017, 37(6): 912-919.

[本文引用: 1]

李净, 王丹, 冯姣姣.

基于 MODIS 遥感产品和神经网络模拟太阳辐射

[J]. 地理科学, 2017, 37(6): 912-919.

[本文引用: 1]

Breiman L.

Random Forests

[J]. Machine Learning, 2001, 45(1): 5-32.

[本文引用: 1]

Breiman L.

Bagging Preditors

[J]. Machine Learning, 1996, 24(2):123-140.

[本文引用: 1]

Fang Kuangnan, Wu Jianbin, Zhu Jianping, et al.

Review of Random Forest Methods Research

[J]. Journal of Statistics and Information, 2011, 26(3): 32-38.

[本文引用: 1]

方匡南, 吴见彬, 朱建平, 等.

随机森林方法研究综述

[J]. 统计与信息论坛, 2011, 26(3):32-38.

[本文引用: 1]

Zhao Lingling, Weng Suming, Zeng Huajun， et al.

Nuclear Method for Pattern Analysis

[M]. Beijing: Mechanical Engineering Press, 2006.赵玲玲, 翁苏明, 曾华军， 等.

模式分析的核方法

[M]. 北京: 机械工程出版社,2006.

[本文引用: 1]

Gao Wei. Principles and Simulation Examples of Artificial Neural Networks [M]. Beijing: Mechanical Engineering Press, 2003.

[本文引用: 1]

高隽.人工神经网络原理及仿真实例[M].北京: 机械工程出版社,2003.

[本文引用: 1]

Vapnik V N. The Nature of Statistical Learning Theory [M].NY: Springer-Verlag, 1995.

[本文引用: 1]

Cortes C，Vapnik V.

Support-vector Network

[J]. Machine Learning，1995，20（3）:273-297.

[本文引用: 1]

Quej V H, Almorox J, Ibrakhimov M, et al.

Empirical Models for Estimating Daily Global Solar Radiation in Yucatán Peninsula, Mexico

[J]. Energy Conversion and Management, 2016, 110: 448-456.

[本文引用: 1]

Meenal R, Selvakumar A I.

Assessment of SVM, Empirical and ANN based Solar Radiation Prediction Models with Most Influencing Input Parameters

[J]. Renewable Energy, 2018, 121: 324-343.

[本文引用: 2]

Feng Jiaojiao, Wang Weizhen, Li Jing, et al.

Analysis of Solar Radiation Simulation and Time-space Change in East China based on BP Neural Network

[J]. Remote Sensing Technology and Application, 2018, 33(5): 881-889.

[本文引用: 1]

冯姣姣, 王维真, 李净, 等.

基于BP神经网络的华东地区太阳辐射模拟及时空变化分析

[J]. 遥感技术与应用, 2018, 33(5):881-889.

[本文引用: 1]

Wei Y, Zhang X, Hou N, et al.

Estimation of Surface Downward Shortwave Radiation over China from AVHRR Data based on Four Machine Learning Methods

[J]. Solar Energy, 2019, 177: 32-46.

[本文引用: 1]

/

〈 〉