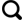1 引 言
合成孔径雷达(SAR)是地表遥感观测体系中的重要手段,利用雷达与目标间相对位置关系变化的相位信息来生成高分辨率影像,不受天气和时间的限制,使其在军事和民用领域得到广泛的应用[1 ] 。对于地面本身具有的移动目标,其运动同样会造成相位信息的变化,这部分变化直接导致成像结果的散焦和移位[2 ,3 ,4 ] 。因此,高精度的目标运动参数估计,对于动目标SAR成像结果的运动补偿以及地面动目标的监测显得尤为重要。
对于SAR场景下运动目标运动参数估计主要从两个角度进行,即图像域和原始回波域[5 ,6 ,7 ,8 ] 。基于图像域的算法为子视图法,但是子视图中动目标是散焦的,所以其结果的精度有待商榷。基于原始回波域的算法为时频分析法和距离历程拟合,后者由于载具运动非理想性,实际中难以进行拟合。SAR回波信号属于线性调频信号,使用时频分析方法可以快速准确的进行分析,故本研究采取时频分析的方法对回波信号进行分析,通过估计回波信号的多普勒中心频率偏移和多普勒调频率来高精度的估计目标地运动参数[9 ,10 ,11 ,12 ] 。
时频分析作为一种有效的线性调频信号分析工具,根据其特性可分为4类:线性时频分析算法,这类算法简单有效,但时频分辨率低[13 ] ;自适应时频分析算法,以希尔伯特—黄变换(Hilbert Huang Transform,HHT)算法为代表的这类的数据驱动的瞬时频率估计方法,受噪声影响严重[14 ] ;能量重排时频算法,以RSPWVD算法为代表的这类算法时频聚集性好,时频分辨率高,但是分析具有相近分量的多分量信号时容易出现散焦[15 ] ;双线性时频分析算法,以维格纳—维尔分布(Wigner-Ville Distribution, WVD)算法为代表的的这类算法具有良好的时频聚集性和高的时频分辨率,使其在SAR回波信号分析这种对时频分辨率要求较高的领域比其他时频分析算法更具有优势,很多学者也开展了一系列基于WVD算法进行SAR回波信号的分析的研究[16 ,17 ,18 ,19 ] 。但是由于WVD算法核函数的双线性,使其对于多分量信号的分析会出现严重的交叉项,影响了其对于信号分量的检测结果。为了抑制交叉项,Wang等[20 ] 联合霍夫(Hough)变换,将时频分析结果由图像空间转换到参数空间进行信号分量的提取。但是,此方法运算量大,而且当噪声较高时,误检率会大幅提升;Wang等[21 ] 利用EMD算法和WVD改进算法进行融合,来消除交叉的影响,但这些融合算法都由于EMD算法的影响,受噪声影响程度大,交叉项去除不干净,不利于实际信号的处理;李秀坤等[22 ] 将WVD算法得到的结果进行坐标转换并滤波,再进行坐标反变换,以消除交叉项。但是,对于特别相近的信号分量之间的交叉项抑制效果不明显。
为了克服上述时频分析算法的缺陷,本文利用HHT算法体系中的EMD算法(并针对抗噪性进行改进)和RSPWVD算法进行融合形成一种新时频分析算法-EMD-RSPWVD算法。多分量SAR回波信号经过改进的EMD算法进行分解,将得到彼此独立的信号分量,对这些独立信号分量分别进行基于RSPWVD算法的时频分析,将能在时频分析结果中有效地区分信号分量,并获得信号分量的相应多普勒信息。本文利用EMD-RSPWVD算法分别对模拟和真实的动目标SAR回波信号进行分析,探究算法的有效性。
2 运动目标回波信号分析
2.1 运动目标SAR回波信号模型
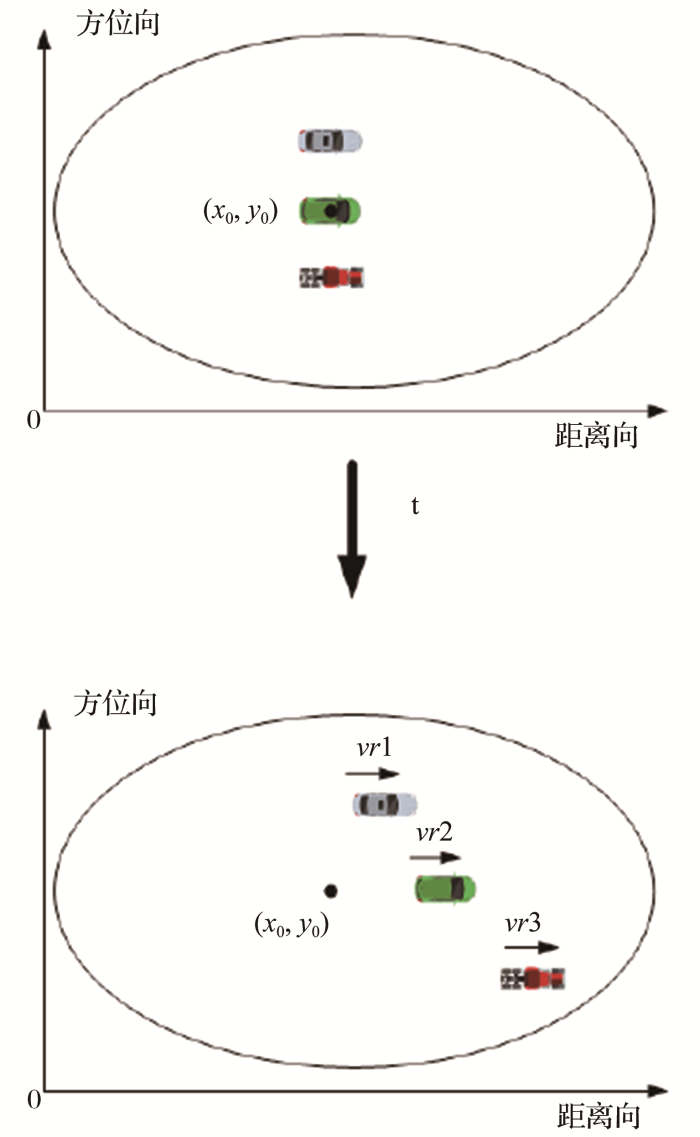
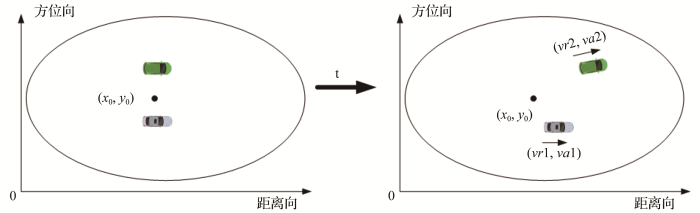
采用机载平台开展运动目标SAR回波信号分析,SAR观测模式为条带式,其正侧视的几何结构如图1 所示。
图1
图1
SAR场景示意图
Fig.1
Schematic diagram of SAR scene
雷达沿着正x 方向以速度v s ( x 0 , y 0 ) v a v r η ( x t , y t ) ( x 0 + v a η , y 0 + v r η , 0 ) ( v s η , 0 , h ) R ( η )
R ( η ) = [ v s η - ( x 0 + v a η ) ] 2 - [ 0 - ( y 0 + v r η ) ] 2 + [ h - 0 ] 2 ≈ R 0 + x 0 v a + y 0 v r - x 0 v s R 0 η + v s 2 + v a 2 + v r 2 - 2 v s v a 2 R 0 η 2 (1)
其中:R 0 = y 0 2 + h 2
S e c h o ( t , η ) = σ 0 ω a ( η ) e x p ( - j 4 π λ R 0 ) ⋅ e x p ( j 2 π [ 1 2 K r ( t - τ ) 2 ] ) ⋅ e x p { - j 4 π ( x 0 v a + y 0 v r - x 0 v s ) λ R 0 η } ⋅ e x p { - j 2 π [ ( v s - v a ) 2 + v r 2 ] 2 λ R 0 η 2 } (2)
其中:σ 0 ω a ( η ) K r t τ 公式(2)中和由目标物运动引起的相位信息变化项的为最后两项。其中,第一项包含距离徙动和多普勒中心偏移有关的信息;第二项包含距离弯曲项和多普勒调频率有关的信息。将获取的经过去载频后的动目标回波信号进行时频分析,从时频分析结果图上获得多普勒中心频率的偏移量和多普勒调频率,进而利用上述后两项反算出移动目标物的方位向速度和距离向速度。由于R 0 t f d c f d r 式(3)和(4):
f d c = 2 x 0 v a λ R 0 (3)
f d r = - 2 ( v s - v r ) 2 λ R 0 (4)
2.2 地面运动目标运动参数估计框架
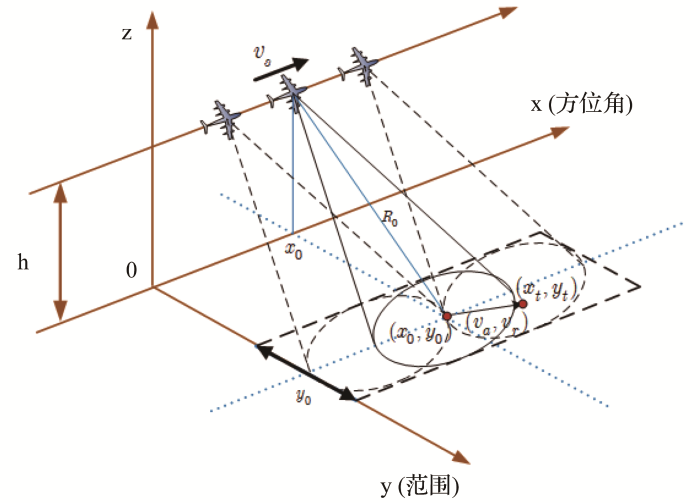
采用正侧视距离多普勒算法对回波数据进行处理,其流程图如图2 ,具体实现步骤为:① ② ③ ④ ⑤
图2
图2
动目标检测及运动参数估计流程图
Fig.2
Flow chart of moving target detection and motion parameter estimation
3 EMD-RSPWVD算法及对比分析
3.1 EMD-RSPWVD算法原理
HHT算法是由数据驱动的一种真正基于瞬时频率的信号自适应分析方法,该算法核心为EMD算法[14 ] 。EMD算法依据数据自身的时间尺度特征将信号分解为若干个从高频到低频排列的固有模态函数(Intrinsic Mode Function,IMF)和一个剩余分量R e s ( t ) 公式(5):
x ( t ) = ∑ i = 1 n I M F i ( t ) + R e s ( t ) (5)
其中:n 表示IMF分量的数量。HHT算法由于在EMD算法分解过程中进行插值操作,如果信号噪声太强会导致插值结果不准确,进而导致HHT算法时频分析结果出现散焦情况。
PWVD算法和SPWVD算法都是对WVD算法分别进行时域或频域平滑的改进算法[21 ] ,其中SPWVD算法是在PWVD算法基础上进行的改进,交叉项抑制效果更好,SPWVD算法的表达式为式(6),该算法对交叉项抑制效果好,但是由于平滑次数多,造成时频分辨率严重下降。RSPWVD算法是由Auger和Flandrin[15 ] 提出,其将重排技术引入到SPWVD算法中,将SPWVD算法时频分析结果局部能量中心由其几何中心重排到其质量中心,这样不仅可以保持时频聚集性,还进一步地压制了交叉项,其时间和瞬时频率的重排表达式为公式(7)和(8):
S P W V D ( t , f ) = ∫ h ( t ) ∫ ω ( t - u ) ⋅ s ( t + τ 2 ) s * ( t - τ 2 ) d u e - j 2 π f t d τ (6)
t ̂ ( x ; t , ω ) = t - ∬ u ⋅ Φ T F ( u , Ω ) S P W V ( x ; t - u , ω - Ω ) d u d Ω 2 π ∬ Φ T F ( u , Ω ) S P W V ( x ; t - u , ω - Ω ) d u d Ω 2 π (7)
ω ̂ ( x ; t , ω ) = ω - ∬ Ω ⋅ Φ T F ( u , Ω ) S P W V ( x ; t - u , ω - Ω ) d u d Ω 2 π ∬ Φ T F ( u , Ω ) S P W V ( x ; t - u , ω - Ω ) d u d Ω 2 π (8)
重排是将局部区域内能量进行重新分布,式(7)和(8)为重排算子,任意一点经重排后其值( t ' , ω ' )
R S P W V D ( x ; t ' , ω ' ) = ∬ S P W V D ( x ; t , ω ) δ ( t ' - t ̂ ( x ; t , ω ) ) ⋅ δ ( ω ' - ω ̂ ( x ; t , ω ) ) d t d ω 2 π (9)
其中:δ ( t )
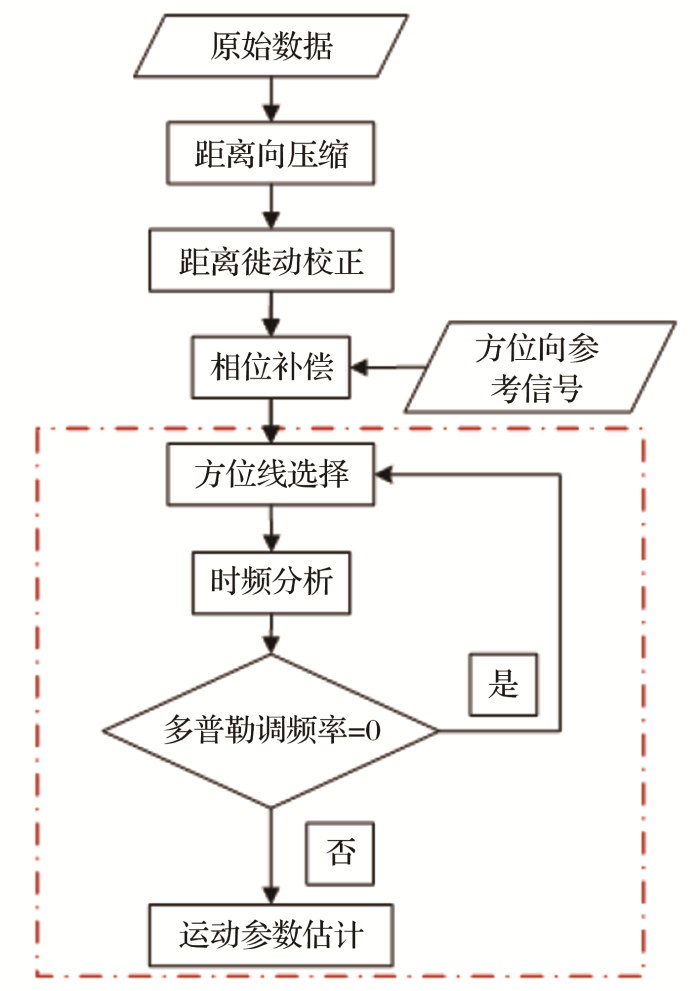
将EMD算法不受交叉项影响的优势和RSPWVD算法高时频聚集性和高时频分辨率的特性结合起来,同时对EMD算法的插值算法进行改进,获得一种既能抑制交叉项又能保持良好时频分辨率和抗噪性的新时频分析算法-EMD-RSPWVD算法。EMD-RSPWVD算法流程图为图3 ,具体处理流程为:① ② ③
图3
图3
EMD-RSPWVD算法流程图
Fig.3
Flow chart of EMD-RSPWVD algorithm
3.2 与已有时频分析算法对比
为了验证EMD-RSPWVD算法对于多分量SAR回波信号分析的有效性,实验设置了一个具有3个运动目标的SAR观测场景——场景1,场景1如图4 所示3个运动目标只有距离向的速度,而且距离向速度分别为3 m/s、6 m/s和9 m/s。实验模拟的是在机载平台下进行,雷达工作波段为C波段,地面目标初始位置设在成像中心,SAR系统的仿真参数如表1 所示。
图4
图4
3个运动目标在场景1中不同时刻位置示意图
Fig.4
Schematic diagram of three moving targets at different moments in scene 1
如图4 所示,实验中目标初始位置都设在一个像元内,这种情景回波数据时频分析较为复杂,EMD-RSPWVD算法如能适用即可进一步推广到其他SAR场景中,进行动目标的检测以及运动目标运动参数估计。将在场景1获得的SAR回波数据进行RDA算法成像处理,选取成像过程中距离压缩后的方位线进行时频分析,分别利用HHT算法、WVD算法、PWVD算法、SPWVD算法、RSPWVD算法、EMD-RSPWVD算法进行对比分析,在数值仿真过程中保持无噪环境,得到的时频分析结果如图5 。
图5
图5
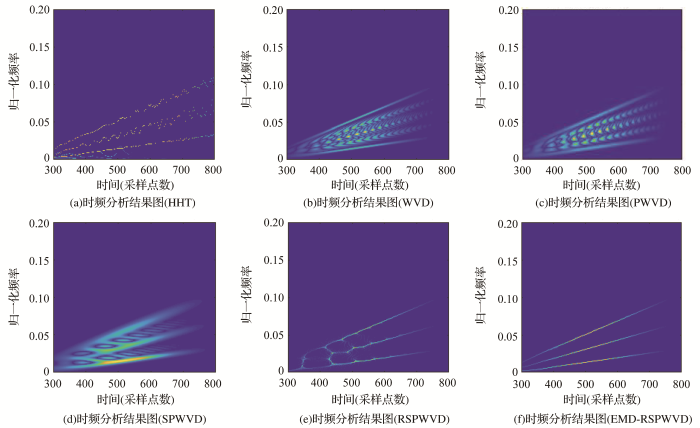
不同时频分析方法处理结果
Fig.5
Different time-frequency analysis method processing results
图5 为在场景1下六种时频分析算法的处理结果,其中,HHT算法对于低频分量能够很好地进行刻画,而对于具有较高频率的分量的刻画出现散焦现象。WVD算法、PWVD算法和SPWVD算法均能够完整的刻画两个位于边缘的分量,但随着平滑次数的增加,其时频分辨率下降严重,同时交叉项没有完全去除,印证了之前理论分析的正确性。RSPWVD算法能够较好地刻画出信号分量,结果保持良好的时频聚集性和时频分辨率,但信号分量频率较为接近的区域会出现混叠现象,不利用后续的多普勒分析。EMD-RSPWVD算法相较于其他5种时频分析方法表现优异,不仅对信号分量刻画完整,而且没有出现交叉项,时频聚集性和时频分辨率都较高,从其时频分析结果图中可以高精度的提取信号分量的多普勒信息,便于后续运动参数的估计分析。
4 实验验证及分析
4.1 动目标检测能力实验与分析
为了验证EMD-RSPWVD算法对于地面移动目标的检测能力,本研究设计一系列场景来进行试验,试验按目标数量分为两目标、三目标、四目标场景。
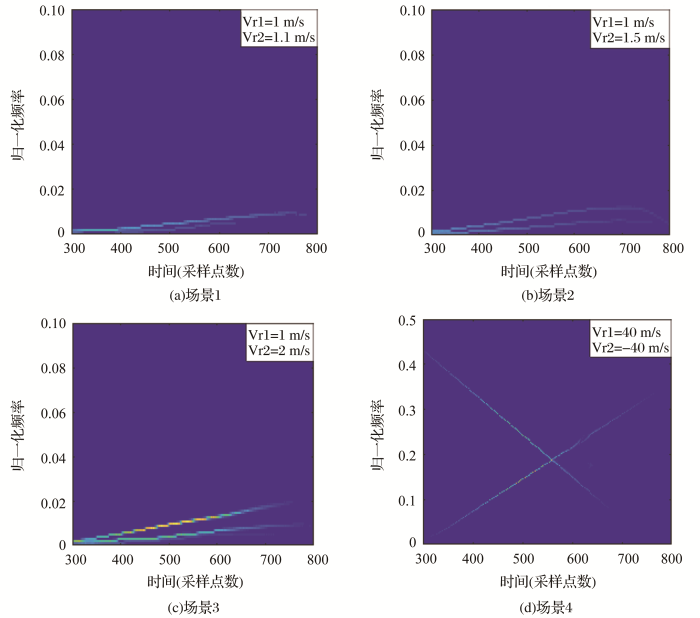
通过设置4个地面有两个运动目标物的场景,进行数值仿真,分析EMD-RSPWVD算法对于存在2个运动目标物场景的检测能力。图6 (a)为运动方向相同且速度相差0.1 m/s的两地面运动目标的SAR回波数据时频分析结果图,图中已可以区分这两个分量,通过计算这两个分量的多普勒参数就可获得两个运动目标的运动参数;图6 (b)为两运动目标运动方向相同且速度相差0.5 m/s的场景,时频分析结果图上可以将二分量很好地区分,并获得两分量精确的多普勒参数;图6 (c)两运动目标运动方向相同且速度相差1 m/s的场景,在时频分析结果图可以将二者完整区分,并可以将两个运动目标的运动参数进行精确估计。图6 (d)为两运动目标运动方向反向的场景,时频分析结果图中频率接近的区域没有出现散焦和混叠现象,同时还能高精度的估计二分量的参数。目标速度达到40 m/s时,时频结果图上的没有出现多普勒混叠,可以证明该算法能够检测的速度范围不小于40 m/s(即144 km/h),足以满足绝大部分地面动目标物检测场景。
图6
图6
地面运动目标物数量为2的4个场景的SAR回波数据时频分析结果图
Fig.6
Time-frequency analysis results of SAR echo data in four scenes with a moving target number of 2
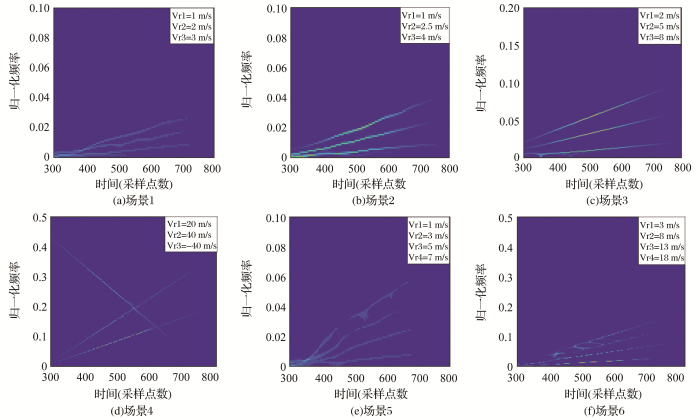
图7 (a)为地面3个运动目标运动方向相同且速度间隔都为1 m/s的场景的时频分析结果,图上3个分量可以得以区分;当3个运动目标速度间隔达到1.5 m/s时,图7 (b)的时频结果图上可以区分3个分量并得到3个目标高精度的运动参数估计;图7 (d)为3个运动目标物中一目标物与另外两目标物运动方向反向的场景,其时频分析结果显示三分量会出现交叉现象,从结果图中可以看出三分量可以得到有效区分,不会出现散焦和混叠现象。图7 (e)和(f)地面运动目标数量为4个的场景,随着目标数量的增加从时频分析结果图上区分各分量的速度间隔逐渐增加。同理对于同方向运动目标不超过4个的场景,EMD-RSPWVD算法均能表现出良好的性能。从实验中也可以得到,当地面动目标物数量较多且速度间隔有限的情况下,在实际应用过程中应取各信号经过EMD分量后的前几个IMF分量进行分析,进而获取各信号分量高精度的多普勒参数估计。
图7
图7
地面移动目标物数量为3和4的6个场景的时频分析结果图
Fig.7
Time-frequency analysis results of 6 scenes with 3 and 4 moving objects on the ground
4.2 仿真数据的运动参数估计实验
由公式(3)和(4)可知,如果已知多普勒中心频率偏移和多普勒调频率的情况下,便可以求出运动目标物的方位向速度和距离向速度,同时也可得出运动目标物的运动方向。多普勒参数可以从时频分析结果图中获得,具体为对时频分析结果图中各分量独立的进行线性拟合,得到各信号分量拟合得到的直线结果及表达式,直线的斜率即为多普勒调频率,进而利用公式(4)推算出地面运动目标物沿距离方向的速度;同时直线的截距推算出多普勒中心频率偏移量,进而就可以利用公式(3)计算出目标沿方位方向移动的速度。在研究中,设计运动速度和方向均不相同的两个运动目标场景——场景2进行仿真分析,场景2中量运动目标的位置示意图如下图8 所示。场景2中目标1只具有距离向速度,速度为5 m/s,目标2同时具有方位向和距离向速度,其速度分别为1 m/s和10 m/s。
图8
图8
SAR场景下两动目标位置示意图
Fig.8
Schematic diagram of two-moving target location in SAR scene
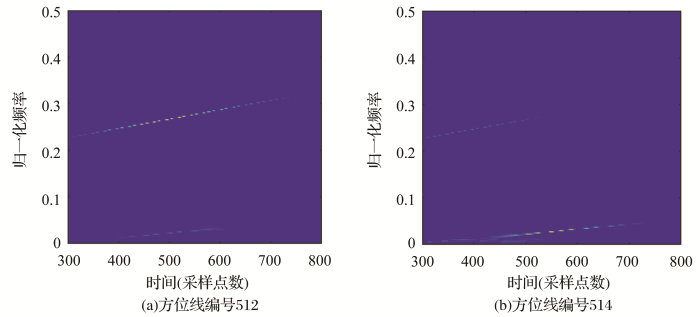
利用EMD-RSPWVD算法对场景2中获取的SAR回波数据进行时频分析,该回波数据是在无噪环境下获得,得到EMD-RSPWVD算法的数值仿真结果如图9 所示。图9 (a)和(b)分别为方位线编号为512和514的两条方位线进行基于EMD-RSPWVD算法,得到的时频分析结果,从结果中可以得知,如果选取中心方位线左侧的方位线进行时频分析,结果会突显频率较高的组分;而选取中心方位线右侧的方位线进行时频分析,其结果会突显频率较低的组分。在实际应用过程中要以多角度去获取信号整体的多普勒特性,进而获得地面动目标物完整的运动参数估计。
图9
图9
两个运动目标EMD-RSPWVD时频分析结果图(方位线编号512、514)
Fig.9
Time-frequency analysis results of EMD-RSPWVD for two moving targets (azimuth line number 512,514)
通过对图8 的EMD-RSPWVD算法的时频分析结果的定量分析,得到场景2中两动目标的运动参数信息,如表2 所示,对于方位向速度的估计误差为0.446 6%,对于距离向的速度估计误差分别达到1.427 1%和3.575 6%。运动目标1为单一在距离方向运动,运动目标2则在距离向和方位向都具有一定速度,可以证实该算法不只可以高精度的估计单一沿距离向或方位向运动的目标的运动参数,还可以高精度的估计任意方向运动的目标的运动参数。
4.3 真实数据的运动参数估计实验
上述实验均在理想环境下进行,但是真实SAR观测过程中,无噪环境是不会存在的,因此需要探究EMD-RSPWVD算法对于噪声的敏感程度,来为下一步真实场景中的应用打基础。设置具有两个运动目标的场景——场景3,场景3中两目标均只具有距离向速度,速度分别为5和10 m/s。通过在场景3中加入不同强度的加性高斯白噪声,分析EMD-RSPWVD算法对于噪声的影响情况。
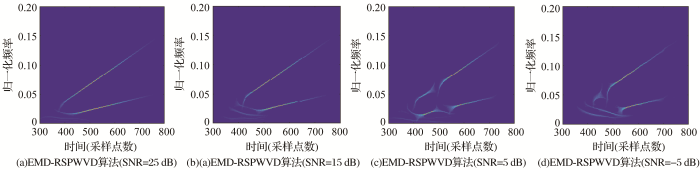
图10 为信噪比为25、15、5和-5 dB的场景3获得的回波数据经过EMD-RSPWVD算法时频分析所获得的结果,从图中可以得知,随着环境噪声的加强,EMD-RSPWVD算法的时频分析结果图中信号分量的低频且相近部分逐渐散焦,而在高频部分依旧保持良好的时频聚集性和时频分辨率。即使在环境噪声达到-5 dB的情形下,两信号分量依旧可以完整区分,并从中通过线性拟合得到信号分量在时频结果图中所应形成的直线,进而获取信号分量的多普勒信息。
图10
图10
EMD-RSPWVD算法抗噪性分析
Fig.10
Analysis of noise resistance of EMD-RSPWVD algorithm
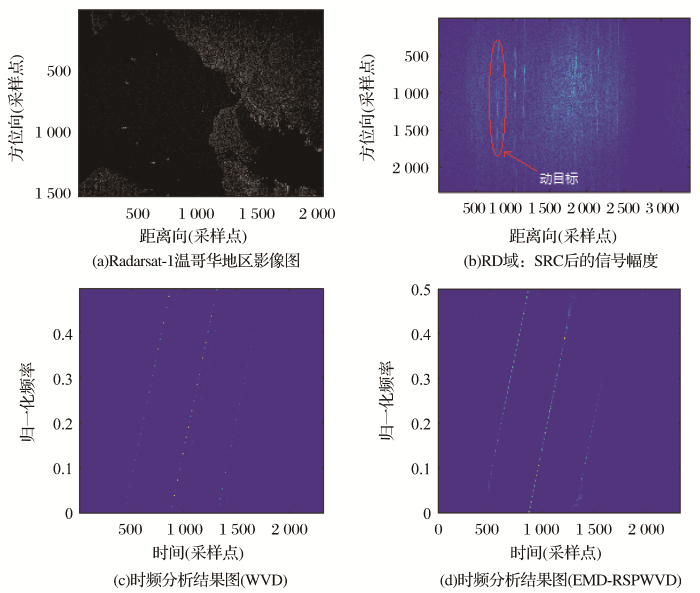
选取2002年温哥华地区的一组Radarsart-1回波数据,来进行真实数据实验与分析。Radarsart-1卫星的系统参数如表3 所示,实验区采用距离多普勒算法进行SAR成像,成像结果如图11 (a)所示。
图11
图11
Radarsat-1真实数据RDA成像结果及时频分析相关结果图
Fig. 11
Radarsat-1 real data RDA imaging results and time-frequency analysis correlation results
图11 (b)为Radarsat-1真实回波数据经过二次距离压缩结果,图中红框所框选区域为动目标所在位置。考虑到雷达速度远远大于地面移动目标物的速度,故在时频分析流程中没有进行方位向相位的补偿,即时频分析结果中多普勒参数的变化是由雷达运动和地面目标运动引起。图11 (c)是基于WVD算法的时频分析结果,可以从图中提取有效的信号分量,但是目标分量旁伴随一条假的分量,可能会造成多普勒参数错误估计。图11 (d)是基于EMD-RSPWVD算法的时频分析结果,图中目标分量的时频聚集性可以达到和WVD算法一样的效果,而且没有虚假分量的存在,同时也表现出EMD-RSPWVD算法良好的抗噪性。Tian等利用同一数据进行地面动目标运动参数估计开展研究,并验证了结果的可靠性,故本实验以其得到的多普勒数据作为参考数据。表4 为实验中EMD-RSPWVD算法所得的多普勒参数与参考数据的对比结果,从表中可以得到基于EMD-RSPWVD算法得到的多普勒参数与参考数据较为接近,验证了EMD-RSPWVD算法对于真实回波数据分析的有效性。
5 结 论
本研究针对SAR场景中现有时频分析算法难以同时准确估计多个运动目标参数的问题,利用改进的EMD算法可以将多分量信号分解为一系列独立信号分量的特性,结合RSPWVD算法良好的时频聚集性以及高时频分辨率的优势,形成一种新的时频分析算法-EMD-RSPWVD算法。与已有时频分析方法相比,EMD-RSPWVD算法具有不受交叉项影响、抗噪性好、时间—频率分辨率高等特性。实验选用模拟SAR回波数据和真实的Radarsat-1回波数据,检验EMD-RSPWVD算法的有效性。实验结果表明新的算法不仅可以有效地区分回波数据中各运动分量,还可以高精度地估计运动目标的运动参数,能为后续动目标SAR成像和属性判别提供关键的速度矢量信息。
对于SAR回波信号这类线性调频脉冲信号体制,EMD-RSPWVD算法表现出良好的性能,未来还将利用EMD-RSPWVD算法对于调频连续波体制、非线性调频信号体制和其他探测信号体制进行进一步的探究。
参考文献
View Option
[1]
Chen K S Principles of Synthetic Aperture Radar Imaging: A System Simulation Approach [M]. Boca Raton : CRC Press , 2016 .
[本文引用: 1]
[2]
Wang Min Yang Fengfeng Liang Diannong et al Distributed Spaceborne SAR-GMTI System Simulation
[J]. Remote Sensing Technology and Application , 2007 , 22 (5 ): 648 -652 .
[本文引用: 1]
王敏 , 杨凤凤 , 梁甸农 , 等 分布式星载SAR-GMTI系统仿真
[J]. 遥感技术与应用 , 2007 , 22 (5 ): 648 -652 .
[本文引用: 1]
[3]
Li G Xu J Peng Y N et al . Detection Velocity Estimation and Imaging of Fast Moving Targets Using Single Antenna SAR
[C] // CIE International Conference on Radar , Shanghai, China : IEEE , 2006 : 1 -4 .
[本文引用: 1]
[4]
Huang P Liao G Yang Z et al A Fast SAR Imaging Method for Ground Moving Target Using a Second-order WVD Transform
[J]. IEEE Transactions on Geoscience and Remote Sensing , 2016 ,54 (4 ):1940 -1956 .
[本文引用: 1]
[5]
Li G Xia X G Xu J et al A Velocity Estimation Algorithm of Moving Targets Using Single Antenna SAR
[J]. IEEE Transactions on Aerospace and Electronic Systems , 2009 , 45 (3 ): 1052 -1062 .
[本文引用: 1]
[6]
Yang Meng Zhu Yutao Zhao Yichao et al A Method based on Wigner-hough Distribution for SAR Ground Moving Target Imaging
[J]. Modern Electronic Technology , 2015 , 38 (17 ):1 -5 .
[本文引用: 1]
杨猛 , 朱宇涛 , 赵逸超 , 等 一种基于Wigner-Hough分布的SAR地面运动目标成像方法
[J].现代电子技术 , 2015 , 38 (17 ):1 -5 ].
[本文引用: 1]
[7]
Xiong Wei Xu Yongli Yao Libo et al A New Ship Target Detection Algorithm based on SVM in High Resolution SAR Images
[J]. Remote Sensing Technology and Application ,2018 ,33 (1 ):119 -127 .
[本文引用: 1]
熊伟 , 徐永力 , 姚力波 ,等 基于SVM的高分辨率SAR图像舰船目标检测算法
[J].遥感技术与应用 ,2018 ,33 (1 ):119 -127 .
[本文引用: 1]
[8]
Wang Na Li Qiangzi Zhao Longcai et al Optimization Analysis in Ship Detection with High-resolution SAR Images based on Variation Coefficient Method
[J]. Remote Sensing Technology and Application ,2017 ,32 (2 ):305 -314 .
[本文引用: 1]
王娜 , 李强子 , 赵龙才 , 等 基于变异系数法的SAR船舶检测优化研究
[J].遥感技术与应用 , 2017 ,32 (2 ):305 -314 .
[本文引用: 1]
[9]
Ding Yu Xue N Munson D C An Analysis of Time-frequency Methods in SAR Imaging of Moving targets
[C] // Proceedings of the 2000 IEEE Sensor Array and Multichannel Signal Processing Workshop . Cambridge, MA, USA , 2000 : 221 –225 .
[本文引用: 1]
[10]
Cexus J C Boudraa A O Nonstationary Signals Analysis by Teager-huang Transform (THT)
[C]// IEEE: 2006 14th European Signal Processing Conference , Florence, Italy , 2006 : 1 -5 .
[本文引用: 1]
[11]
Sun H B Liu G S Gu H et al Application of the Fractional Fourier Transform to Moving Target Detection in Airborne SAR
[J]. IEEE Transactions on Aerospace and Electronic Systems , 2002 , 38 (4 ):1416 -1424 .
[本文引用: 1]
[12]
Yeh C Yang J Shan X M et al Simultaneous Range and Radial Velocity Estimation with a Single Narrowband LFM Pulse
[J]. Journal of Systems Engineering and Electronics , 2012 ,23 (3 ):372 -377 .
[本文引用: 1]
[13]
Zhang Jun Zhang Zhiyong Chen Xueguang A Speckle Suppressed and Reduction Technology for SAR Images
[J]. Remote Sensing Technology and Application , 1998 , 13 (3 ): 44 -47 .
[本文引用: 1]
张俊 , 张志勇 , 陈学广 SAR图像斑点噪声抑制与滤除技术
[J]. 遥感技术与应用 , 1998 , 13 (3 ): 44 -47 .
[本文引用: 1]
[14]
Chen V C Miceli W J Time-varying Spectral Analysis for Radar Imaging of Maneuvering Targets
[J]. IEE Proceedings-Radar , Sonar and Navigation , 1998 , 145 (15 ): 262 -268 .
[本文引用: 2]
[15]
Auger F Flandrin P Improving the Readability of Time-frequency and Time-scale Representations by the Reassignment Method
[J]. IEEE Transactions on Signal Processing , 1995 , 43 (5 ):1068 -1089 .
[本文引用: 2]
[16]
Barbarossa S Farina A Detection and Imaging of Moving Objects with Synthetic Aperture Radar. Part 1: Joint Time-frequency Analysis by Wigner-ville Distribution
[J]. IEE Proceedings F (Radar and Signal Processing) , 1992 , 139 (1 ): 79 -88 .
[本文引用: 1]
[17]
Barbarossa S Farina A Detection and Imaging of Moving Objects with Synthetic Aperture Radar. Part 2: Joint Time-frequency Analysis by Wigner-ville Distribution
[J]. IEE Proceedings F (Radar and Signal Processing) ,1992 , 39 (1 ): 89 -97 .
[本文引用: 1]
[18]
Wang H Jiang Y Real-time Parameter Estimation for SAR Moving Target based on WVD Slice and FrFT
[J]. Electronics Letters , 2017 , 54 (1 ): 47 -49 .
[本文引用: 1]
[19]
Huang P Liao G Yang Z et al A Fast SAR Imaging Method for Ground Moving Target Using a Second-order WVD Transform
[J]. IEEE Transactions on Geoscience and Remote Sensing , 2016 , 54 (4 ): 1940 -1956 .
[本文引用: 1]
[20]
Wang H Fan X Chen Y et al Wigner-hough Transform based on Slice'S Entropy and Its Application to Multi-LFM Signal Detection
[J]. Journal of Systems Engineering and Electronics , 2017 , 28 (4 ): 634 -642 .
[本文引用: 1]
[21]
Wang Y Wu X Li W et al Analysis of Micro-Doppler Signatures of Vibration Targets Using EMD and SPWVD
[J]. Neurocomputing , 2015 , 171 (C ):48 -56 .
[本文引用: 2]
[22]
Li Xiukun Wu Yushuang Removal of Cross-terms of Wigner-ville Distribution for Multi-component Chirp Signals
[J]. Chinese Journal of Electronics , 2017 , 45 (2 ): 316 -320 .
[本文引用: 1]
李秀坤 , 吴玉双 多分量线性调频信号的Wigner-Ville分布交叉项去除
[J]. 电子学报 , 2017 , 45 (2 ): 316 -320 .
[本文引用: 1]
[23]
Tian J Cui W Xia X G et al Parameter Estimation of Ground Moving Targets based on SKT-DLVT Processing
[J]. IEEE Transactions on Computational Imaging , 2016 , 2 (1 ):13 -26 .
1
2016
... 合成孔径雷达(SAR)是地表遥感观测体系中的重要手段,利用雷达与目标间相对位置关系变化的相位信息来生成高分辨率影像,不受天气和时间的限制,使其在军事和民用领域得到广泛的应用[1 ] .对于地面本身具有的移动目标,其运动同样会造成相位信息的变化,这部分变化直接导致成像结果的散焦和移位[2 ,3 ,4 ] .因此,高精度的目标运动参数估计,对于动目标SAR成像结果的运动补偿以及地面动目标的监测显得尤为重要. ...
分布式星载SAR-GMTI系统仿真
1
2007
... 合成孔径雷达(SAR)是地表遥感观测体系中的重要手段,利用雷达与目标间相对位置关系变化的相位信息来生成高分辨率影像,不受天气和时间的限制,使其在军事和民用领域得到广泛的应用[1 ] .对于地面本身具有的移动目标,其运动同样会造成相位信息的变化,这部分变化直接导致成像结果的散焦和移位[2 ,3 ,4 ] .因此,高精度的目标运动参数估计,对于动目标SAR成像结果的运动补偿以及地面动目标的监测显得尤为重要. ...
分布式星载SAR-GMTI系统仿真
1
2007
... 合成孔径雷达(SAR)是地表遥感观测体系中的重要手段,利用雷达与目标间相对位置关系变化的相位信息来生成高分辨率影像,不受天气和时间的限制,使其在军事和民用领域得到广泛的应用[1 ] .对于地面本身具有的移动目标,其运动同样会造成相位信息的变化,这部分变化直接导致成像结果的散焦和移位[2 ,3 ,4 ] .因此,高精度的目标运动参数估计,对于动目标SAR成像结果的运动补偿以及地面动目标的监测显得尤为重要. ...
Velocity Estimation and Imaging of Fast Moving Targets Using Single Antenna SAR
1
2006
... 合成孔径雷达(SAR)是地表遥感观测体系中的重要手段,利用雷达与目标间相对位置关系变化的相位信息来生成高分辨率影像,不受天气和时间的限制,使其在军事和民用领域得到广泛的应用[1 ] .对于地面本身具有的移动目标,其运动同样会造成相位信息的变化,这部分变化直接导致成像结果的散焦和移位[2 ,3 ,4 ] .因此,高精度的目标运动参数估计,对于动目标SAR成像结果的运动补偿以及地面动目标的监测显得尤为重要. ...
A Fast SAR Imaging Method for Ground Moving Target Using a Second-order WVD Transform
1
2016
... 合成孔径雷达(SAR)是地表遥感观测体系中的重要手段,利用雷达与目标间相对位置关系变化的相位信息来生成高分辨率影像,不受天气和时间的限制,使其在军事和民用领域得到广泛的应用[1 ] .对于地面本身具有的移动目标,其运动同样会造成相位信息的变化,这部分变化直接导致成像结果的散焦和移位[2 ,3 ,4 ] .因此,高精度的目标运动参数估计,对于动目标SAR成像结果的运动补偿以及地面动目标的监测显得尤为重要. ...
A Velocity Estimation Algorithm of Moving Targets Using Single Antenna SAR
1
2009
... 对于SAR场景下运动目标运动参数估计主要从两个角度进行,即图像域和原始回波域[5 ,6 ,7 ,8 ] .基于图像域的算法为子视图法,但是子视图中动目标是散焦的,所以其结果的精度有待商榷.基于原始回波域的算法为时频分析法和距离历程拟合,后者由于载具运动非理想性,实际中难以进行拟合.SAR回波信号属于线性调频信号,使用时频分析方法可以快速准确的进行分析,故本研究采取时频分析的方法对回波信号进行分析,通过估计回波信号的多普勒中心频率偏移和多普勒调频率来高精度的估计目标地运动参数[9 ,10 ,11 ,12 ] . ...
一种基于Wigner-Hough分布的SAR地面运动目标成像方法
1
2015
... 对于SAR场景下运动目标运动参数估计主要从两个角度进行,即图像域和原始回波域[5 ,6 ,7 ,8 ] .基于图像域的算法为子视图法,但是子视图中动目标是散焦的,所以其结果的精度有待商榷.基于原始回波域的算法为时频分析法和距离历程拟合,后者由于载具运动非理想性,实际中难以进行拟合.SAR回波信号属于线性调频信号,使用时频分析方法可以快速准确的进行分析,故本研究采取时频分析的方法对回波信号进行分析,通过估计回波信号的多普勒中心频率偏移和多普勒调频率来高精度的估计目标地运动参数[9 ,10 ,11 ,12 ] . ...
一种基于Wigner-Hough分布的SAR地面运动目标成像方法
1
2015
... 对于SAR场景下运动目标运动参数估计主要从两个角度进行,即图像域和原始回波域[5 ,6 ,7 ,8 ] .基于图像域的算法为子视图法,但是子视图中动目标是散焦的,所以其结果的精度有待商榷.基于原始回波域的算法为时频分析法和距离历程拟合,后者由于载具运动非理想性,实际中难以进行拟合.SAR回波信号属于线性调频信号,使用时频分析方法可以快速准确的进行分析,故本研究采取时频分析的方法对回波信号进行分析,通过估计回波信号的多普勒中心频率偏移和多普勒调频率来高精度的估计目标地运动参数[9 ,10 ,11 ,12 ] . ...
基于SVM的高分辨率SAR图像舰船目标检测算法
1
2018
... 对于SAR场景下运动目标运动参数估计主要从两个角度进行,即图像域和原始回波域[5 ,6 ,7 ,8 ] .基于图像域的算法为子视图法,但是子视图中动目标是散焦的,所以其结果的精度有待商榷.基于原始回波域的算法为时频分析法和距离历程拟合,后者由于载具运动非理想性,实际中难以进行拟合.SAR回波信号属于线性调频信号,使用时频分析方法可以快速准确的进行分析,故本研究采取时频分析的方法对回波信号进行分析,通过估计回波信号的多普勒中心频率偏移和多普勒调频率来高精度的估计目标地运动参数[9 ,10 ,11 ,12 ] . ...
基于SVM的高分辨率SAR图像舰船目标检测算法
1
2018
... 对于SAR场景下运动目标运动参数估计主要从两个角度进行,即图像域和原始回波域[5 ,6 ,7 ,8 ] .基于图像域的算法为子视图法,但是子视图中动目标是散焦的,所以其结果的精度有待商榷.基于原始回波域的算法为时频分析法和距离历程拟合,后者由于载具运动非理想性,实际中难以进行拟合.SAR回波信号属于线性调频信号,使用时频分析方法可以快速准确的进行分析,故本研究采取时频分析的方法对回波信号进行分析,通过估计回波信号的多普勒中心频率偏移和多普勒调频率来高精度的估计目标地运动参数[9 ,10 ,11 ,12 ] . ...
基于变异系数法的SAR船舶检测优化研究
1
2017
... 对于SAR场景下运动目标运动参数估计主要从两个角度进行,即图像域和原始回波域[5 ,6 ,7 ,8 ] .基于图像域的算法为子视图法,但是子视图中动目标是散焦的,所以其结果的精度有待商榷.基于原始回波域的算法为时频分析法和距离历程拟合,后者由于载具运动非理想性,实际中难以进行拟合.SAR回波信号属于线性调频信号,使用时频分析方法可以快速准确的进行分析,故本研究采取时频分析的方法对回波信号进行分析,通过估计回波信号的多普勒中心频率偏移和多普勒调频率来高精度的估计目标地运动参数[9 ,10 ,11 ,12 ] . ...
基于变异系数法的SAR船舶检测优化研究
1
2017
... 对于SAR场景下运动目标运动参数估计主要从两个角度进行,即图像域和原始回波域[5 ,6 ,7 ,8 ] .基于图像域的算法为子视图法,但是子视图中动目标是散焦的,所以其结果的精度有待商榷.基于原始回波域的算法为时频分析法和距离历程拟合,后者由于载具运动非理想性,实际中难以进行拟合.SAR回波信号属于线性调频信号,使用时频分析方法可以快速准确的进行分析,故本研究采取时频分析的方法对回波信号进行分析,通过估计回波信号的多普勒中心频率偏移和多普勒调频率来高精度的估计目标地运动参数[9 ,10 ,11 ,12 ] . ...
An Analysis of Time-frequency Methods in SAR Imaging of Moving targets
1
2000
... 对于SAR场景下运动目标运动参数估计主要从两个角度进行,即图像域和原始回波域[5 ,6 ,7 ,8 ] .基于图像域的算法为子视图法,但是子视图中动目标是散焦的,所以其结果的精度有待商榷.基于原始回波域的算法为时频分析法和距离历程拟合,后者由于载具运动非理想性,实际中难以进行拟合.SAR回波信号属于线性调频信号,使用时频分析方法可以快速准确的进行分析,故本研究采取时频分析的方法对回波信号进行分析,通过估计回波信号的多普勒中心频率偏移和多普勒调频率来高精度的估计目标地运动参数[9 ,10 ,11 ,12 ] . ...
Nonstationary Signals Analysis by Teager-huang Transform (THT)
1
2006
... 对于SAR场景下运动目标运动参数估计主要从两个角度进行,即图像域和原始回波域[5 ,6 ,7 ,8 ] .基于图像域的算法为子视图法,但是子视图中动目标是散焦的,所以其结果的精度有待商榷.基于原始回波域的算法为时频分析法和距离历程拟合,后者由于载具运动非理想性,实际中难以进行拟合.SAR回波信号属于线性调频信号,使用时频分析方法可以快速准确的进行分析,故本研究采取时频分析的方法对回波信号进行分析,通过估计回波信号的多普勒中心频率偏移和多普勒调频率来高精度的估计目标地运动参数[9 ,10 ,11 ,12 ] . ...
Application of the Fractional Fourier Transform to Moving Target Detection in Airborne SAR
1
2002
... 对于SAR场景下运动目标运动参数估计主要从两个角度进行,即图像域和原始回波域[5 ,6 ,7 ,8 ] .基于图像域的算法为子视图法,但是子视图中动目标是散焦的,所以其结果的精度有待商榷.基于原始回波域的算法为时频分析法和距离历程拟合,后者由于载具运动非理想性,实际中难以进行拟合.SAR回波信号属于线性调频信号,使用时频分析方法可以快速准确的进行分析,故本研究采取时频分析的方法对回波信号进行分析,通过估计回波信号的多普勒中心频率偏移和多普勒调频率来高精度的估计目标地运动参数[9 ,10 ,11 ,12 ] . ...
Simultaneous Range and Radial Velocity Estimation with a Single Narrowband LFM Pulse
1
2012
... 对于SAR场景下运动目标运动参数估计主要从两个角度进行,即图像域和原始回波域[5 ,6 ,7 ,8 ] .基于图像域的算法为子视图法,但是子视图中动目标是散焦的,所以其结果的精度有待商榷.基于原始回波域的算法为时频分析法和距离历程拟合,后者由于载具运动非理想性,实际中难以进行拟合.SAR回波信号属于线性调频信号,使用时频分析方法可以快速准确的进行分析,故本研究采取时频分析的方法对回波信号进行分析,通过估计回波信号的多普勒中心频率偏移和多普勒调频率来高精度的估计目标地运动参数[9 ,10 ,11 ,12 ] . ...
SAR图像斑点噪声抑制与滤除技术
1
1998
... 时频分析作为一种有效的线性调频信号分析工具,根据其特性可分为4类:线性时频分析算法,这类算法简单有效,但时频分辨率低[13 ] ;自适应时频分析算法,以希尔伯特—黄变换(Hilbert Huang Transform,HHT)算法为代表的这类的数据驱动的瞬时频率估计方法,受噪声影响严重[14 ] ;能量重排时频算法,以RSPWVD算法为代表的这类算法时频聚集性好,时频分辨率高,但是分析具有相近分量的多分量信号时容易出现散焦[15 ] ;双线性时频分析算法,以维格纳—维尔分布(Wigner-Ville Distribution, WVD)算法为代表的的这类算法具有良好的时频聚集性和高的时频分辨率,使其在SAR回波信号分析这种对时频分辨率要求较高的领域比其他时频分析算法更具有优势,很多学者也开展了一系列基于WVD算法进行SAR回波信号的分析的研究[16 ,17 ,18 ,19 ] .但是由于WVD算法核函数的双线性,使其对于多分量信号的分析会出现严重的交叉项,影响了其对于信号分量的检测结果.为了抑制交叉项,Wang等[20 ] 联合霍夫(Hough)变换,将时频分析结果由图像空间转换到参数空间进行信号分量的提取.但是,此方法运算量大,而且当噪声较高时,误检率会大幅提升;Wang等[21 ] 利用EMD算法和WVD改进算法进行融合,来消除交叉的影响,但这些融合算法都由于EMD算法的影响,受噪声影响程度大,交叉项去除不干净,不利于实际信号的处理;李秀坤等[22 ] 将WVD算法得到的结果进行坐标转换并滤波,再进行坐标反变换,以消除交叉项.但是,对于特别相近的信号分量之间的交叉项抑制效果不明显. ...
SAR图像斑点噪声抑制与滤除技术
1
1998
... 时频分析作为一种有效的线性调频信号分析工具,根据其特性可分为4类:线性时频分析算法,这类算法简单有效,但时频分辨率低[13 ] ;自适应时频分析算法,以希尔伯特—黄变换(Hilbert Huang Transform,HHT)算法为代表的这类的数据驱动的瞬时频率估计方法,受噪声影响严重[14 ] ;能量重排时频算法,以RSPWVD算法为代表的这类算法时频聚集性好,时频分辨率高,但是分析具有相近分量的多分量信号时容易出现散焦[15 ] ;双线性时频分析算法,以维格纳—维尔分布(Wigner-Ville Distribution, WVD)算法为代表的的这类算法具有良好的时频聚集性和高的时频分辨率,使其在SAR回波信号分析这种对时频分辨率要求较高的领域比其他时频分析算法更具有优势,很多学者也开展了一系列基于WVD算法进行SAR回波信号的分析的研究[16 ,17 ,18 ,19 ] .但是由于WVD算法核函数的双线性,使其对于多分量信号的分析会出现严重的交叉项,影响了其对于信号分量的检测结果.为了抑制交叉项,Wang等[20 ] 联合霍夫(Hough)变换,将时频分析结果由图像空间转换到参数空间进行信号分量的提取.但是,此方法运算量大,而且当噪声较高时,误检率会大幅提升;Wang等[21 ] 利用EMD算法和WVD改进算法进行融合,来消除交叉的影响,但这些融合算法都由于EMD算法的影响,受噪声影响程度大,交叉项去除不干净,不利于实际信号的处理;李秀坤等[22 ] 将WVD算法得到的结果进行坐标转换并滤波,再进行坐标反变换,以消除交叉项.但是,对于特别相近的信号分量之间的交叉项抑制效果不明显. ...
Time-varying Spectral Analysis for Radar Imaging of Maneuvering Targets
2
1998
... 时频分析作为一种有效的线性调频信号分析工具,根据其特性可分为4类:线性时频分析算法,这类算法简单有效,但时频分辨率低[13 ] ;自适应时频分析算法,以希尔伯特—黄变换(Hilbert Huang Transform,HHT)算法为代表的这类的数据驱动的瞬时频率估计方法,受噪声影响严重[14 ] ;能量重排时频算法,以RSPWVD算法为代表的这类算法时频聚集性好,时频分辨率高,但是分析具有相近分量的多分量信号时容易出现散焦[15 ] ;双线性时频分析算法,以维格纳—维尔分布(Wigner-Ville Distribution, WVD)算法为代表的的这类算法具有良好的时频聚集性和高的时频分辨率,使其在SAR回波信号分析这种对时频分辨率要求较高的领域比其他时频分析算法更具有优势,很多学者也开展了一系列基于WVD算法进行SAR回波信号的分析的研究[16 ,17 ,18 ,19 ] .但是由于WVD算法核函数的双线性,使其对于多分量信号的分析会出现严重的交叉项,影响了其对于信号分量的检测结果.为了抑制交叉项,Wang等[20 ] 联合霍夫(Hough)变换,将时频分析结果由图像空间转换到参数空间进行信号分量的提取.但是,此方法运算量大,而且当噪声较高时,误检率会大幅提升;Wang等[21 ] 利用EMD算法和WVD改进算法进行融合,来消除交叉的影响,但这些融合算法都由于EMD算法的影响,受噪声影响程度大,交叉项去除不干净,不利于实际信号的处理;李秀坤等[22 ] 将WVD算法得到的结果进行坐标转换并滤波,再进行坐标反变换,以消除交叉项.但是,对于特别相近的信号分量之间的交叉项抑制效果不明显. ...
... HHT算法是由数据驱动的一种真正基于瞬时频率的信号自适应分析方法,该算法核心为EMD算法[14 ] .EMD算法依据数据自身的时间尺度特征将信号分解为若干个从高频到低频排列的固有模态函数(Intrinsic Mode Function,IMF)和一个剩余分量R e s ( t ) 公式(5) : ...
Improving the Readability of Time-frequency and Time-scale Representations by the Reassignment Method
2
1995
... 时频分析作为一种有效的线性调频信号分析工具,根据其特性可分为4类:线性时频分析算法,这类算法简单有效,但时频分辨率低[13 ] ;自适应时频分析算法,以希尔伯特—黄变换(Hilbert Huang Transform,HHT)算法为代表的这类的数据驱动的瞬时频率估计方法,受噪声影响严重[14 ] ;能量重排时频算法,以RSPWVD算法为代表的这类算法时频聚集性好,时频分辨率高,但是分析具有相近分量的多分量信号时容易出现散焦[15 ] ;双线性时频分析算法,以维格纳—维尔分布(Wigner-Ville Distribution, WVD)算法为代表的的这类算法具有良好的时频聚集性和高的时频分辨率,使其在SAR回波信号分析这种对时频分辨率要求较高的领域比其他时频分析算法更具有优势,很多学者也开展了一系列基于WVD算法进行SAR回波信号的分析的研究[16 ,17 ,18 ,19 ] .但是由于WVD算法核函数的双线性,使其对于多分量信号的分析会出现严重的交叉项,影响了其对于信号分量的检测结果.为了抑制交叉项,Wang等[20 ] 联合霍夫(Hough)变换,将时频分析结果由图像空间转换到参数空间进行信号分量的提取.但是,此方法运算量大,而且当噪声较高时,误检率会大幅提升;Wang等[21 ] 利用EMD算法和WVD改进算法进行融合,来消除交叉的影响,但这些融合算法都由于EMD算法的影响,受噪声影响程度大,交叉项去除不干净,不利于实际信号的处理;李秀坤等[22 ] 将WVD算法得到的结果进行坐标转换并滤波,再进行坐标反变换,以消除交叉项.但是,对于特别相近的信号分量之间的交叉项抑制效果不明显. ...
... PWVD算法和SPWVD算法都是对WVD算法分别进行时域或频域平滑的改进算法[21 ] ,其中SPWVD算法是在PWVD算法基础上进行的改进,交叉项抑制效果更好,SPWVD算法的表达式为式(6) ,该算法对交叉项抑制效果好,但是由于平滑次数多,造成时频分辨率严重下降.RSPWVD算法是由Auger和Flandrin[15 ] 提出,其将重排技术引入到SPWVD算法中,将SPWVD算法时频分析结果局部能量中心由其几何中心重排到其质量中心,这样不仅可以保持时频聚集性,还进一步地压制了交叉项,其时间和瞬时频率的重排表达式为公式(7) 和(8): ...
Detection and Imaging of Moving Objects with Synthetic Aperture Radar. Part 1: Joint Time-frequency Analysis by Wigner-ville Distribution
1
1992
... 时频分析作为一种有效的线性调频信号分析工具,根据其特性可分为4类:线性时频分析算法,这类算法简单有效,但时频分辨率低[13 ] ;自适应时频分析算法,以希尔伯特—黄变换(Hilbert Huang Transform,HHT)算法为代表的这类的数据驱动的瞬时频率估计方法,受噪声影响严重[14 ] ;能量重排时频算法,以RSPWVD算法为代表的这类算法时频聚集性好,时频分辨率高,但是分析具有相近分量的多分量信号时容易出现散焦[15 ] ;双线性时频分析算法,以维格纳—维尔分布(Wigner-Ville Distribution, WVD)算法为代表的的这类算法具有良好的时频聚集性和高的时频分辨率,使其在SAR回波信号分析这种对时频分辨率要求较高的领域比其他时频分析算法更具有优势,很多学者也开展了一系列基于WVD算法进行SAR回波信号的分析的研究[16 ,17 ,18 ,19 ] .但是由于WVD算法核函数的双线性,使其对于多分量信号的分析会出现严重的交叉项,影响了其对于信号分量的检测结果.为了抑制交叉项,Wang等[20 ] 联合霍夫(Hough)变换,将时频分析结果由图像空间转换到参数空间进行信号分量的提取.但是,此方法运算量大,而且当噪声较高时,误检率会大幅提升;Wang等[21 ] 利用EMD算法和WVD改进算法进行融合,来消除交叉的影响,但这些融合算法都由于EMD算法的影响,受噪声影响程度大,交叉项去除不干净,不利于实际信号的处理;李秀坤等[22 ] 将WVD算法得到的结果进行坐标转换并滤波,再进行坐标反变换,以消除交叉项.但是,对于特别相近的信号分量之间的交叉项抑制效果不明显. ...
Detection and Imaging of Moving Objects with Synthetic Aperture Radar. Part 2: Joint Time-frequency Analysis by Wigner-ville Distribution
1
1992
... 时频分析作为一种有效的线性调频信号分析工具,根据其特性可分为4类:线性时频分析算法,这类算法简单有效,但时频分辨率低[13 ] ;自适应时频分析算法,以希尔伯特—黄变换(Hilbert Huang Transform,HHT)算法为代表的这类的数据驱动的瞬时频率估计方法,受噪声影响严重[14 ] ;能量重排时频算法,以RSPWVD算法为代表的这类算法时频聚集性好,时频分辨率高,但是分析具有相近分量的多分量信号时容易出现散焦[15 ] ;双线性时频分析算法,以维格纳—维尔分布(Wigner-Ville Distribution, WVD)算法为代表的的这类算法具有良好的时频聚集性和高的时频分辨率,使其在SAR回波信号分析这种对时频分辨率要求较高的领域比其他时频分析算法更具有优势,很多学者也开展了一系列基于WVD算法进行SAR回波信号的分析的研究[16 ,17 ,18 ,19 ] .但是由于WVD算法核函数的双线性,使其对于多分量信号的分析会出现严重的交叉项,影响了其对于信号分量的检测结果.为了抑制交叉项,Wang等[20 ] 联合霍夫(Hough)变换,将时频分析结果由图像空间转换到参数空间进行信号分量的提取.但是,此方法运算量大,而且当噪声较高时,误检率会大幅提升;Wang等[21 ] 利用EMD算法和WVD改进算法进行融合,来消除交叉的影响,但这些融合算法都由于EMD算法的影响,受噪声影响程度大,交叉项去除不干净,不利于实际信号的处理;李秀坤等[22 ] 将WVD算法得到的结果进行坐标转换并滤波,再进行坐标反变换,以消除交叉项.但是,对于特别相近的信号分量之间的交叉项抑制效果不明显. ...
Real-time Parameter Estimation for SAR Moving Target based on WVD Slice and FrFT
1
2017
... 时频分析作为一种有效的线性调频信号分析工具,根据其特性可分为4类:线性时频分析算法,这类算法简单有效,但时频分辨率低[13 ] ;自适应时频分析算法,以希尔伯特—黄变换(Hilbert Huang Transform,HHT)算法为代表的这类的数据驱动的瞬时频率估计方法,受噪声影响严重[14 ] ;能量重排时频算法,以RSPWVD算法为代表的这类算法时频聚集性好,时频分辨率高,但是分析具有相近分量的多分量信号时容易出现散焦[15 ] ;双线性时频分析算法,以维格纳—维尔分布(Wigner-Ville Distribution, WVD)算法为代表的的这类算法具有良好的时频聚集性和高的时频分辨率,使其在SAR回波信号分析这种对时频分辨率要求较高的领域比其他时频分析算法更具有优势,很多学者也开展了一系列基于WVD算法进行SAR回波信号的分析的研究[16 ,17 ,18 ,19 ] .但是由于WVD算法核函数的双线性,使其对于多分量信号的分析会出现严重的交叉项,影响了其对于信号分量的检测结果.为了抑制交叉项,Wang等[20 ] 联合霍夫(Hough)变换,将时频分析结果由图像空间转换到参数空间进行信号分量的提取.但是,此方法运算量大,而且当噪声较高时,误检率会大幅提升;Wang等[21 ] 利用EMD算法和WVD改进算法进行融合,来消除交叉的影响,但这些融合算法都由于EMD算法的影响,受噪声影响程度大,交叉项去除不干净,不利于实际信号的处理;李秀坤等[22 ] 将WVD算法得到的结果进行坐标转换并滤波,再进行坐标反变换,以消除交叉项.但是,对于特别相近的信号分量之间的交叉项抑制效果不明显. ...
A Fast SAR Imaging Method for Ground Moving Target Using a Second-order WVD Transform
1
2016
... 时频分析作为一种有效的线性调频信号分析工具,根据其特性可分为4类:线性时频分析算法,这类算法简单有效,但时频分辨率低[13 ] ;自适应时频分析算法,以希尔伯特—黄变换(Hilbert Huang Transform,HHT)算法为代表的这类的数据驱动的瞬时频率估计方法,受噪声影响严重[14 ] ;能量重排时频算法,以RSPWVD算法为代表的这类算法时频聚集性好,时频分辨率高,但是分析具有相近分量的多分量信号时容易出现散焦[15 ] ;双线性时频分析算法,以维格纳—维尔分布(Wigner-Ville Distribution, WVD)算法为代表的的这类算法具有良好的时频聚集性和高的时频分辨率,使其在SAR回波信号分析这种对时频分辨率要求较高的领域比其他时频分析算法更具有优势,很多学者也开展了一系列基于WVD算法进行SAR回波信号的分析的研究[16 ,17 ,18 ,19 ] .但是由于WVD算法核函数的双线性,使其对于多分量信号的分析会出现严重的交叉项,影响了其对于信号分量的检测结果.为了抑制交叉项,Wang等[20 ] 联合霍夫(Hough)变换,将时频分析结果由图像空间转换到参数空间进行信号分量的提取.但是,此方法运算量大,而且当噪声较高时,误检率会大幅提升;Wang等[21 ] 利用EMD算法和WVD改进算法进行融合,来消除交叉的影响,但这些融合算法都由于EMD算法的影响,受噪声影响程度大,交叉项去除不干净,不利于实际信号的处理;李秀坤等[22 ] 将WVD算法得到的结果进行坐标转换并滤波,再进行坐标反变换,以消除交叉项.但是,对于特别相近的信号分量之间的交叉项抑制效果不明显. ...
Wigner-hough Transform based on Slice'S Entropy and Its Application to Multi-LFM Signal Detection
1
2017
... 时频分析作为一种有效的线性调频信号分析工具,根据其特性可分为4类:线性时频分析算法,这类算法简单有效,但时频分辨率低[13 ] ;自适应时频分析算法,以希尔伯特—黄变换(Hilbert Huang Transform,HHT)算法为代表的这类的数据驱动的瞬时频率估计方法,受噪声影响严重[14 ] ;能量重排时频算法,以RSPWVD算法为代表的这类算法时频聚集性好,时频分辨率高,但是分析具有相近分量的多分量信号时容易出现散焦[15 ] ;双线性时频分析算法,以维格纳—维尔分布(Wigner-Ville Distribution, WVD)算法为代表的的这类算法具有良好的时频聚集性和高的时频分辨率,使其在SAR回波信号分析这种对时频分辨率要求较高的领域比其他时频分析算法更具有优势,很多学者也开展了一系列基于WVD算法进行SAR回波信号的分析的研究[16 ,17 ,18 ,19 ] .但是由于WVD算法核函数的双线性,使其对于多分量信号的分析会出现严重的交叉项,影响了其对于信号分量的检测结果.为了抑制交叉项,Wang等[20 ] 联合霍夫(Hough)变换,将时频分析结果由图像空间转换到参数空间进行信号分量的提取.但是,此方法运算量大,而且当噪声较高时,误检率会大幅提升;Wang等[21 ] 利用EMD算法和WVD改进算法进行融合,来消除交叉的影响,但这些融合算法都由于EMD算法的影响,受噪声影响程度大,交叉项去除不干净,不利于实际信号的处理;李秀坤等[22 ] 将WVD算法得到的结果进行坐标转换并滤波,再进行坐标反变换,以消除交叉项.但是,对于特别相近的信号分量之间的交叉项抑制效果不明显. ...
Analysis of Micro-Doppler Signatures of Vibration Targets Using EMD and SPWVD
2
2015
... 时频分析作为一种有效的线性调频信号分析工具,根据其特性可分为4类:线性时频分析算法,这类算法简单有效,但时频分辨率低[13 ] ;自适应时频分析算法,以希尔伯特—黄变换(Hilbert Huang Transform,HHT)算法为代表的这类的数据驱动的瞬时频率估计方法,受噪声影响严重[14 ] ;能量重排时频算法,以RSPWVD算法为代表的这类算法时频聚集性好,时频分辨率高,但是分析具有相近分量的多分量信号时容易出现散焦[15 ] ;双线性时频分析算法,以维格纳—维尔分布(Wigner-Ville Distribution, WVD)算法为代表的的这类算法具有良好的时频聚集性和高的时频分辨率,使其在SAR回波信号分析这种对时频分辨率要求较高的领域比其他时频分析算法更具有优势,很多学者也开展了一系列基于WVD算法进行SAR回波信号的分析的研究[16 ,17 ,18 ,19 ] .但是由于WVD算法核函数的双线性,使其对于多分量信号的分析会出现严重的交叉项,影响了其对于信号分量的检测结果.为了抑制交叉项,Wang等[20 ] 联合霍夫(Hough)变换,将时频分析结果由图像空间转换到参数空间进行信号分量的提取.但是,此方法运算量大,而且当噪声较高时,误检率会大幅提升;Wang等[21 ] 利用EMD算法和WVD改进算法进行融合,来消除交叉的影响,但这些融合算法都由于EMD算法的影响,受噪声影响程度大,交叉项去除不干净,不利于实际信号的处理;李秀坤等[22 ] 将WVD算法得到的结果进行坐标转换并滤波,再进行坐标反变换,以消除交叉项.但是,对于特别相近的信号分量之间的交叉项抑制效果不明显. ...
... PWVD算法和SPWVD算法都是对WVD算法分别进行时域或频域平滑的改进算法[21 ] ,其中SPWVD算法是在PWVD算法基础上进行的改进,交叉项抑制效果更好,SPWVD算法的表达式为式(6) ,该算法对交叉项抑制效果好,但是由于平滑次数多,造成时频分辨率严重下降.RSPWVD算法是由Auger和Flandrin[15 ] 提出,其将重排技术引入到SPWVD算法中,将SPWVD算法时频分析结果局部能量中心由其几何中心重排到其质量中心,这样不仅可以保持时频聚集性,还进一步地压制了交叉项,其时间和瞬时频率的重排表达式为公式(7) 和(8): ...
多分量线性调频信号的Wigner-Ville分布交叉项去除
1
2017
... 时频分析作为一种有效的线性调频信号分析工具,根据其特性可分为4类:线性时频分析算法,这类算法简单有效,但时频分辨率低[13 ] ;自适应时频分析算法,以希尔伯特—黄变换(Hilbert Huang Transform,HHT)算法为代表的这类的数据驱动的瞬时频率估计方法,受噪声影响严重[14 ] ;能量重排时频算法,以RSPWVD算法为代表的这类算法时频聚集性好,时频分辨率高,但是分析具有相近分量的多分量信号时容易出现散焦[15 ] ;双线性时频分析算法,以维格纳—维尔分布(Wigner-Ville Distribution, WVD)算法为代表的的这类算法具有良好的时频聚集性和高的时频分辨率,使其在SAR回波信号分析这种对时频分辨率要求较高的领域比其他时频分析算法更具有优势,很多学者也开展了一系列基于WVD算法进行SAR回波信号的分析的研究[16 ,17 ,18 ,19 ] .但是由于WVD算法核函数的双线性,使其对于多分量信号的分析会出现严重的交叉项,影响了其对于信号分量的检测结果.为了抑制交叉项,Wang等[20 ] 联合霍夫(Hough)变换,将时频分析结果由图像空间转换到参数空间进行信号分量的提取.但是,此方法运算量大,而且当噪声较高时,误检率会大幅提升;Wang等[21 ] 利用EMD算法和WVD改进算法进行融合,来消除交叉的影响,但这些融合算法都由于EMD算法的影响,受噪声影响程度大,交叉项去除不干净,不利于实际信号的处理;李秀坤等[22 ] 将WVD算法得到的结果进行坐标转换并滤波,再进行坐标反变换,以消除交叉项.但是,对于特别相近的信号分量之间的交叉项抑制效果不明显. ...
多分量线性调频信号的Wigner-Ville分布交叉项去除
1
2017
... 时频分析作为一种有效的线性调频信号分析工具,根据其特性可分为4类:线性时频分析算法,这类算法简单有效,但时频分辨率低[13 ] ;自适应时频分析算法,以希尔伯特—黄变换(Hilbert Huang Transform,HHT)算法为代表的这类的数据驱动的瞬时频率估计方法,受噪声影响严重[14 ] ;能量重排时频算法,以RSPWVD算法为代表的这类算法时频聚集性好,时频分辨率高,但是分析具有相近分量的多分量信号时容易出现散焦[15 ] ;双线性时频分析算法,以维格纳—维尔分布(Wigner-Ville Distribution, WVD)算法为代表的的这类算法具有良好的时频聚集性和高的时频分辨率,使其在SAR回波信号分析这种对时频分辨率要求较高的领域比其他时频分析算法更具有优势,很多学者也开展了一系列基于WVD算法进行SAR回波信号的分析的研究[16 ,17 ,18 ,19 ] .但是由于WVD算法核函数的双线性,使其对于多分量信号的分析会出现严重的交叉项,影响了其对于信号分量的检测结果.为了抑制交叉项,Wang等[20 ] 联合霍夫(Hough)变换,将时频分析结果由图像空间转换到参数空间进行信号分量的提取.但是,此方法运算量大,而且当噪声较高时,误检率会大幅提升;Wang等[21 ] 利用EMD算法和WVD改进算法进行融合,来消除交叉的影响,但这些融合算法都由于EMD算法的影响,受噪声影响程度大,交叉项去除不干净,不利于实际信号的处理;李秀坤等[22 ] 将WVD算法得到的结果进行坐标转换并滤波,再进行坐标反变换,以消除交叉项.但是,对于特别相近的信号分量之间的交叉项抑制效果不明显. ...
Parameter Estimation of Ground Moving Targets based on SKT-DLVT Processing
0
2016