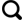青藏高原GPM降水数据空间降尺度研究

doi:10.11873/j.issn.1004-0323.2021.3.0571

青藏高原GPM降水数据空间降尺度研究

盛夏^,, 石玉立^,, 丁海勇

南京信息工程大学遥感与测绘工程学院，江苏南京 210044

Spatial Downscaling of GPM Precipitation over the Tibetan Plateau

Sheng Xia^,, Shi Yuli^,, Ding Haiyong

School of Remote Sensing & Geomatics Engineering，Nanjing University of Information Science&Technology，Nanjing 210044，China

通讯作者: 石玉立(1973-),男，河南卫辉人，博士，教授,主要从事森林地上生物量遥感反演研究。E⁃mail：ylshi@nusit.edu.cn

收稿日期: 2020-04-17 修回日期: 2021-04-16 网络出版日期: 2021-07-21

基金资助:

国家自然科学基金项目“异速增长和资源限制模型结合多源遥感数据估算森林地上生物量研究”. 41471312
国家自然科学基金项目 “城市边缘区地表组分温度反演模型的构建”. 41571350

Received: 2020-04-17 Revised: 2021-04-16 Online: 2021-07-21

作者简介 About authors

盛夏（1995-），女，江苏扬州人，硕士研究生，主要从事遥感降水降尺度研究E⁃mail:20171206339@nuist.edu.cn , E-mail：20171206339@nuist.edu.cn

摘要

高分辨率的降水数据对于复杂地形区的精确水文预报和气候模拟至关重要。利用青藏高原的植被、地形和地理位置特征，建立了与降水的回归模型，将全球降水测量（GPM）IMERG的年降水量从0.1° 降尺度至1 km，通过分解年降水获得月降水量数据，并用气象站点的实测数据进行校准。得出以下结论：①GPM IMERG月降水量略大于地面观测值，与2015~2017年的站点数据相关性较高（R²=0.79）；②通过建立降尺度模型，提高了研究区GPM IMERG的空间分辨率；③利用站点数据校准后的月降水量，可以反映降水的细节特征，尤其是在雨季和湿润地区。该模型可用于获得地形复杂地区的高空间分辨率降水资料，对水文学和气象学研究具有重要意义。

关键词： GPM ; 降尺度 ; 降水 ; 青藏高原 ; 随机森林

Abstract

Precipitation dataset with high resolution are essential for accurate hydrology predictions and meteorology simulations over complex terrains. A regression model was built to downscale the Global Precipitation Measurement （GPM） IMERG precipitation data from 0.1° to 1 km on an annual scale， using vegetation， topography and geographical location features over the Tibetan Plateau. Then monthly precipitation data were obtained by disaggregating the annual downscaled estimates， which were calibrated with observations of local rain gauge stations. The major conclusions are summarized as follows：（1） Monthly GPM IMERG precipitation demonstrated good agreement with the rain gauge data during the period 2015 to 2017 （R²=0.79）， though GPM was slightly larger than ground observations；（2） Annual downscaled precipitation improved the spatial resolution of the GPM IMERG in the study area；（3） Monthly donscaled precipitation calibrated with rain gauge data reflected detailed characteristics with better predictive performance especially in summer or in wet regions.We concluded that the model can be used to obtain precipitation data with high spatial resolution from heavy rain to light one over the areas with complex tography， which is meaning for applications in hydrology and metorology studies.

Keywords： Global Precipitation Measurement （GPM） ; Downscale ; Precipitation ; Tibetan Plateau ; Random Forest.

PDF (2799KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

盛夏, 石玉立, 丁海勇. 青藏高原GPM降水数据空间降尺度研究. 遥感技术与应用[J], 2021, 36(3): 571-580 doi:10.11873/j.issn.1004-0323.2021.3.0571

Sheng Xia, Shi Yuli, Ding Haiyong. Spatial Downscaling of GPM Precipitation over the Tibetan Plateau. Remote Sensing Technology and Application[J], 2021, 36(3): 571-580 doi:10.11873/j.issn.1004-0323.2021.3.0571

1 引言

降水是全球水循环的重要组成部分，对水文和气象过程具有重要影响^［1］。准确的降水数据在水资源管理、天气预报、灾害监测与评估等各个应用领域都是重要的状态变量。

青藏高原具有海拔高、地形地质条件复杂、气候环境独特等特点，以青藏高原为中心的地区，是众多河流的发源地，有“亚洲水塔”之称，获取高山区的高分辨率降水，有助于水资源管理和研究气候变化的区域响应。然而，青藏高原区域的气象站数量稀少且多分布在东南地区，通过站点数据插值获取连续降水的精度难以保证。卫星遥感数据能提供该地区连续的高空间分辨率降水数据，弥补了地面观测的不足。随着遥感技术的发展，已经有一系列基于卫星的降水观测数据集用于降水相关研究，如CMORPH（Climate Prediction Center morphing technique）^［2］，GPCP（Global Precipitation Climatology Project）^［3］，TRMM（Tropical Rainfall Measuring Mission）^［4］，GSMaP（Global Satellite Mapping of Precipitation Project）^［5］和GPM（Global Precipitation Measurement）^［6］等。TRMM数据集可以提供0.25°空间分辨率的热带和亚热带地区的大中型降水信息，被广泛应用于各个领域，GPM扩展了TRMM传感载荷，时空分辨率进一步提高。但是当进一步研究区域降水的时空分布特征时，卫星降水数据的分辨率还不能满足部分研究需求，因此有必要对降水数据进行空间降尺度研究。

降尺度的方法主要有4种，分别是简单降尺度法、统计降尺度法、动力降尺度法以及动力和统计相结合降尺度法，其中统计降尺度法由于计算效率高，且下垫面特征可以控制模型参数，因此应用较为广泛^［7］。Immerzeel等^［8］通过建立归一化植被指数（NDVI）与TRMM降水的指数模型，获取了伊比利亚半岛1 km空间分辨率的年降水量。Park^［9］在Immerzeel等的基础上建立了TRMM与NDVI、数字高程模型（DEM）之间的数量关系，结果显示经过降尺度操作的数据能够体现更细致的特征。刘小婵等^［10］应用地理加权回归模型（GWR）进行降尺度研究，证明该模型比最小二乘法模型更适用于东北地区。玉院和等^［11］将云南省的TRMM 3B43降水数据降尺度至季、年尺度并对经度进行了评价。而对于新一代GPM产品，国内外学者也开展了研究工作。魏志明等^［12］在月尺度上比较了海河流域TRMM和GPM数据的精度，结果表明GPM精度高于TRMM数据，但两者均低估了海河流域的降水量。Anastasios-Petro等^［13］利用希腊2016年的气象站点观测结果，评估了GPM近实时日产品的多卫星联合反演精度，结果显示GPM产品与观测结果有较好的一致性，但高估了降水量。冯克鹏等^［14］运用GPM IMERG等7种卫星降水产品用于驱动水文模型，发现了GPM IMERG的效果较优。

国内外关于获取青藏高原地区的高时空分辨率降水数据做过许多研究，例如刘文丰等^［15］利用ASD统计降尺度方法雅鲁藏布江流域的降水和气温进行降尺度，并分析了未来气候变化情况；Jing等^［16］采用随机森林和支持向量机两种机器学习算法，将TRMM 3B43 V7降水数据从25 km降尺度到1km；熊俊楠等^［17］基于GWR模型实现2001~2015年间的TRMM产品的降尺度处理。以往关于GPM降水数据研究集中在评价IMERG数据的质量和直接应用研究，对于尺度转换方面的研究较少。Zhang等^［18］利用地面站点的小时观测数据，对GPM和TMPA降水产品的精度进行统计评估；李兰辉等^［19］基于自动观测站降水数据和包括IMERG在内的5套降水格点产品，对羌塘高原的降水时空分布格局进行分析。

综上所述，目前对青藏高原地区的卫星降水数据精度评价的研究较多，将GPM降水数据和地面站点数据相结合的降尺度研究较少。因此，综合考虑植被、地形和地理位置要素，建立降水与NDVI、高程、坡度、坡向、经度和纬度这6个辅助因子之间的随机森林模型，对青藏高原地区2015~2017年GPM数据进行降尺度操作，并利用研究区的地面观测数据进行校正。研究的目标是：①用统计降尺度方法将青藏高原2015~2017年的GPM降水量空间分辨率提升至1 km×1 km；②分别比较GPM和TRMM降水数据在月尺度上的表现；③研究GPM数据对弱降水的响应。

2 研究区和数据

2.1　研究区域

青藏高原地处中国西南地区，介于26°00′12″~39°46′50″ N、73°18′52″~104°46′59″ E之间，平均海拔4 000 m以上，面积约为 $2.57 \times 10^{6}$ km²，是地球上最大的高原地区（图1）。青藏高原水文气候过程主要受西风和印度洋季风控制，部分东部区域，还受到微弱的亚洲东南季风的影响。青藏高原降水在时间、空间上分布不均，降水的空间分布呈现自东南向西北递减、自南向北减少的格局，80%以上的降水发生在夏季（6~8月），特别是青藏高原东南部主要受夏季印度洋季风控制，这给该地区带来了湿润的气候和大量降水（年降水量在400~2 000 mm）。大部分中部地区降水受到西风和印度洋季风共同影响，气候较湿润，降水量相对丰富（年降水量约为400~800 mm）。而北部、西北部和大部分西部主要受西风带的控制，形成了干旱或半干旱气候（年降水量小于200 mm）^［20］。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 青藏高原高程及气象站点分布图

Fig.1 Elevation of the Tibetan Plateau and distribution of rainfall stations

2.2　数据介绍及预处理

2.2.1　GPM和TRMM数据

GPM是由美国和日本联合研发的新一代全球卫星降水计划，由一个核心观测平台和八颗伙伴卫星组成，携带了双频降水雷达和微波成像仪。选用2015~2017年间空间分辨率为0.1°的GPM IMERG （Integrated Multi-satellite Retrievals for GPM）月降水产品（https：//pmm.nasa.gov/data-access/downloads/gpm），对青藏高原地区进行降水降尺度研究。TRMM提供了一系列算法处理后的产品，其中3B43 V7数据集的空间分辨率为0.25°，时间分辨率为月，适用于全球50° N~50° S地区。实验选用2015~2017年间的TRMM 3B43 V7降水数据，下载于http：//pmm.nasa.gov/data-acces/downloads/trmm。

2.2.2　站点实测数据

地面气象站点数据下载于中国气象数据网（http：//data.cma.cn/）。青藏高原地区109个站点降水数据的空间分布如图1所示，可以看出这些站点在整个研究区中分布不均。采用2015年1月至2017年12月的日降水量记录，各站点的月降水量和年降水量由日降水量累加计算得到，用于验证和校正原始遥感降水数据和降尺度模型获取的降水数据。

2.2.3　归一化植被指数数据

中分辨率成像光谱仪MODIS的NDVI数据的时空覆盖范围广，可提供全球绝大部分地区的中尺度分辨率观测数据。采用美国国家地质调查局（USGS）和美国国家航空航天局（NASA）联合组建的陆地产品分发中心（LPDAAC）发布的MOD13A3产品，其提供每月1 km分辨率的产品，通过计算12个月NDVI数据的平均值作为年NDVI值。

2.2.4　SRTM DEM数据

DEM数据是从美国太空总署（NASA）和国防部国家测绘局（NIMA）共同测量的航天飞机地貌雷达任务（Shuttle Radar Topography Mission， SRTM）中获取数据的。其数据范围在南北纬60° 之间，选用的产品空间分辨率是90 m。该数据下载于http：∥www.gscloud.cn/。采用ArcGIS10.2软件拼接下载的所有研究区内的90 m分辨率SRTM数据，再利用青藏高原的边界裁切，从而得到该地区的SRTM数据。根据SRTM数据可以直接获取高程信息，在此基础上获取坡度和坡向信息。

3 研究方法

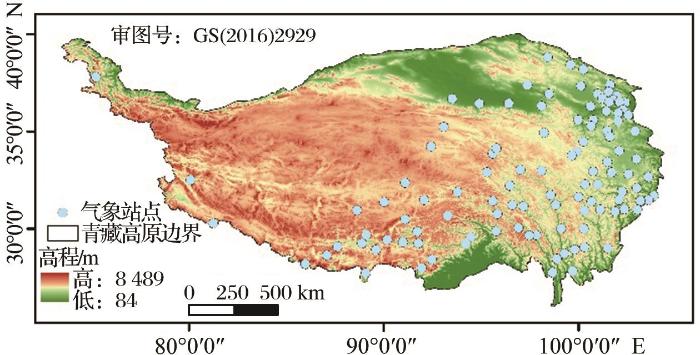
统计降尺度也称为经验降尺度，是利用经验方法构建大尺度变量与区域变量之间的线性或非线性关系，进而进行尺度间的转化^［21］。已有的研究表明，随机森林是建立降水量与地理空间因子之间相关关系的有效算法，特别是在地形复杂的地区^［22］。

采用基于随机森林回归模型的降尺度方法，获取高空间分辨率的年降水量数据。主要步骤如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 GPM数据降尺度流程图

Fig.2 Flowchart of spatial downscaling of GPM precipitation

（1）将年NDVI、高程、坡度和坡向分别重采样至0.1°，并提取相应网格的经纬度信息。

（2）高程、坡度、坡向、经度、纬度、NDVI作为自变量，GPM IMERG年累计降水数据作为因变量，在0.1° 的尺度上构建降尺度模型。

（3）将高程、坡度和坡向均重采样至1 km，输入建立的模型中，得到2015~2017年1 km分辨率的年降水。

（4）利用Duan等^［23］提出的比例系数法，根据原始GPM降水数据获取各月降水占相应年降水的比例系数，将年降水分解为各月降水。

（5）采用地理差异分析（GDA）方法^［24］对月估算降水进行校正，即计算站点实测月降水量与模拟月降水之间的差异，运用普通克里格法将误差值插值成1 km栅格数据，与模拟月降水量相加，获取经过站点校正的1 km分辨率月降尺度降水数据。

3.1　随机森林算法

随机森林（Random Forest）是分类回归树（Classification And Regression Tree，CART）的扩展，可以提高CART模型的准确性和稳定性^［25］。CART模型回归时遍历数据集S中的每个样本的每个值，找到用于将原始数据集S分成S1和S2两个样本子集合的最佳分割特征和分割值，从而使S1和S2总平方误差之和（SSE）最小化：

S S E = \sum_{i \in S_{1}} {(y_{i} - {\bar{y}}_{1})}^{2} + \sum_{i \in S_{2}} {(y_{i} - {\bar{y}}_{2})}^{2}

（1）

其中： ${\bar{y}}_{1}$ 和 ${\bar{y}}_{2}$ 分别表示S1和S2子集合的样本的平均值。重复这一过程直到分割中的样本数低于某个阈值。

随机森林算法是从原始数据集中使用bootstrap方法随机分割成多个样本子集ntree，对于每个样本子集，随机选择mtry个特征，对回归而言，取对每棵树ntree预测结果的平均值作为最后预测值^［26］。将降水数据与高程、经度、纬度、坡度、坡向和NDVI数据输入随机森林模型，建立降水量与其他相关因子之间的关系，使用了R语言中提供的randomForest package来建立回归模型。

3.2　克里金插值法

克里金插值法又叫地学统计法，是南非矿山工程师克里金在寻找金矿时提出。克里金插值以区域变化量理论为基础，利用半变异函数得到最佳权重系数，从而获得最优估计值^［27］。经过发展，普通克里金方法出现了多种变化，如协同克里金法、指示克里金法、泛克里金法等。普通克里金的定义如下：

\hat{z} (x_{0}) = \sum_{i = 1}^{n} λ_{i} z (x_{i})

（2）

其中： $\hat{z} (x_{0})$ 是非采样位置 $x_{0}$ 处的克里金估计值， $z (x_{i})$ 是 $x_{i}$ 处的样本点值， $λ_{i}$ 是权重因子，权重因子需要满足以下条件：

\sum_{i = 1}^{n} λ_{i} = 1

（3）

在无偏约束条件下，误差的最小方差定义为：

σ^{2} = V a r [\hat{z} (x_{0}) - z (x_{0})]

（4）

其中： $σ^{2}$ 为误差方差， $z (x_{0})$ 为 $x_{0}$ 处的未知真值。

在对离散气象站点进行空间插值获取全局数据时，克里金插值的应用相当广泛，本文应用普通克里金法对降水量进行校正。

3.3　结果验证

为了评估青藏高原地区的原始卫星降水数据和降尺度结果的有效性，综合考虑以往点观测降水资料验证栅格降水资料的指标选取^［28］，选用了决定系数 $R^{2}$ 、均方根误差RMSE、平均绝对误差MAE、偏差Bias 4个指标用于精度评价。

（1）决定系数 $R^{2}$ 。表示站点实测降水值与降水数据的相关密切程度，越接近1时，降尺度结果效果越好。

R^{2} = {(\sum_{i = 1}^{n} \frac{(S_{i} - \bar{S}) (P_{i} - \bar{P})}{\sqrt[]{\sum_{i = 1}^{n} {(S_{i} - S)}^{2} {(P_{i} - \bar{P})}^{2}}})}^{2}

（5）

（2）均方根误差RMSE。站点实测降水值与降水数据之差平方的期望值的算术平方根，值越小，模型精确度越高。

R M S E = \sqrt[]{\frac{\sum_{i = 1}^{n} {(S_{i} - P_{i})}^{2}}{n}}

（6）

（3）平均绝对误差MAE。站点实测降水值与降水数据之差的绝对值的平均，反映模型预测值误差的实际情况。

M A E = \frac{\sum_{i = 1}^{n} |S_{i} - P_{i}|}{n}

（7）

（4）偏差Bias。降水数据与站点实测值之间的差距。

B i a s = \frac{\sum_{i = 1}^{n} P_{i}}{\sum_{i = 1}^{n} S_{i}} - 1

（8）

其中： $S_{i}$ 为第i个站点实测降水量； $\bar{S}$ 为站点实测降水平均值； $P_{i}$ 为模型模拟第i个站点的降水量， $\bar{P}$ 为模型模拟降水平均值， $n$ 为验证模型的地面观测站点的个数。

4 结果分析与检验

4.1　GPM数据的有效性检验

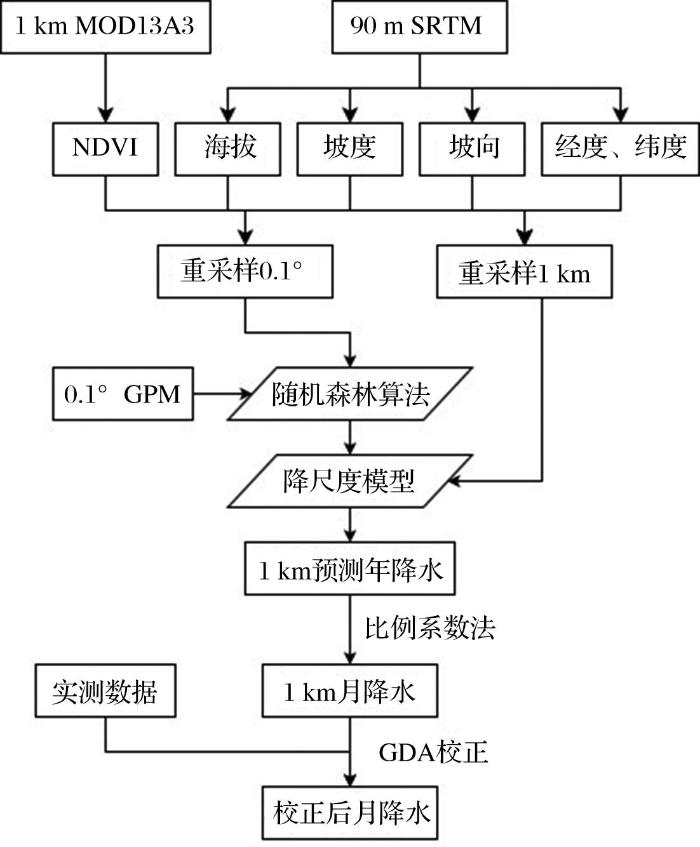
利用青藏高原地区2015~2017年109个雨量站点（图1）的观测数据作为降水量的“真实值”，对比了2015~2017年间GPM IMERG和TRMM 3B43月降水数据与对应站点处降水量的相关性（图3）。从图中可以看出，GPM和TRMM都高估了降水，其中GPM的Bias值为11.75%，TRMM的Bias值为13.15%； GPM和TRMM与地面站点的相关性较好，GPM数据与地面站点的决定系数R²为0.79， TRMM与地面站点的决定系数R²为0.73；大多数散点落在1∶1线附近，同时存在一些离群点，它们的实测月降水都在300 mm以上，但相应站点处的卫星降水数值明显偏低，反映了卫星降水数据对一些强降水的低估问题，GPM月降水的低估现象有所改善。这可能是因为降水雷达遇到强降水时发生较大的衰减，与TRMM的单频雷达相比，GPM搭载的双频降水雷达算法能够提供瞬时面降雨和垂直水汽廓线及其在网格上的时空累积量，衰减较小，对降水有更高的敏感性^［6，29］。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 地面站点与GPM IMERG、TRMM3B43月降水数据的散点图

Fig.3 Scatter plots of the measured monthly precipitation from rain gauge stations versus the monthly estimates from GPM IMERG， and TRMM 3B43 during the study period over the Tibetan Plateau， respectively

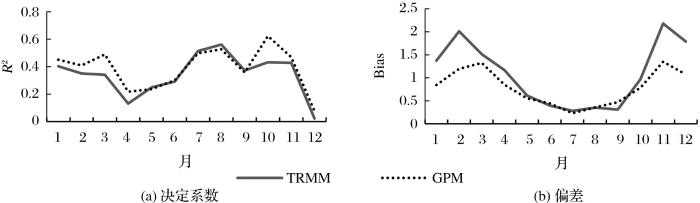
为了检验在月降水尺度上两代产品的差异，选取2015~2017年平均年降水量小于400 mm的站点（表1），进一步分析TRMM和GPM的数据精度。从表中可以看出，大部分的地面气象站点观测值与GPM和TRMM数据之间存在较高的决定系数。对符合条件的32个地面气象站点2015~2017年逐月进行趋势分析，图4绘制了GPM和TRMM卫星的月降水数据与实测月降水的决定系数R²和偏差Bias的折线图。从图中可以看出，GPM在干季与实际降水的决定系数明显高于TRMM，而在雨季两代产品差异较小整体表现一致。GPM和TRMM均表现出对实际降水的高估，除9月份TRMM与实测月降水的偏差与GPM相比更小以外，其他月份GPM的高估程度都小于TRMM或与TRMM相近，说明在总降水量较少的地区GPM明显优于TRMM。GPM数据在干旱地区观测降水更准确的原因可能是搭载的两大传感器载荷的性能提升，其中微波成像仪扩展了频率范围（10~183 GHz），高频段更适合观测小雨和降雪，双频降水雷达增加的Ka波段（38.5 GHz）提升了观测微小降水和固态降水的能力，能更好地区分降雪和降水^［6，30］。

表1 GPM、TRMM月降水数据与地面站点降水量决定系数（年降水量小于400 mm的32个站点）

Table1 32 rain gauge stations in the areas with annual precipitation less than 400 mm/a， and coefficient of determination calculated between GPM， TRMM precipitation products and ground measurements at monthly scale

站点名	TRMM	GPM	平均年降水量/mm	站点名	TRMM	GPM	平均年降水量/mm
托勒	0.80	0.81	372.77	同仁	0.81	0.76	357.97
海西州	0.84	0.88	357.60	曲麻莱	0.87	0.84	351.03
刚察	0.92	0.98	144.00	玛多	0.92	0.87	342.10
门源	0.79	0.83	257.27	治多	0.86	0.92	346.53
乌兰	0.86	0.69	64.67	日喀则	0.95	0.95	363.30
塔什库尔干	0.05	0.57	113.87	海东	0.84	0.84	268.97
茶卡	0.69	0.73	287.07	尼木	0.88	0.92	311.93
兴海	0.72	0.75	297.97	泽当	0.93	0.93	398.73
安多	0.71	0.79	110.03	隆子	0.85	0.90	296.57
西宁	0.85	0.93	375.53	拉孜	0.91	0.91	335.50
同德	0.69	0.79	341.83	江孜	0.80	0.88	274.77
恰卜恰	0.65	0.83	246.97	得荣	0.84	0.82	341.13
托托河	0.88	0.96	296.17	定日	0.91	0.85	243.80
伍道梁	0.83	0.90	335.20	八宿	0.61	0.76	210.07
都兰	0.73	0.72	59.47	帕里	0.83	0.83	399.60
那曲	0.93	0.96	226.03	小灶火	0.74	0.77	31.77

新窗口打开| 下载CSV

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 GPM、TRMM月降水数据的决定系数（R²）、偏差（Bias）序列图

Fig.4 Coefficient of determination and Bias of monthly precipitation estimates from GPM and TRMM

4.2　年降水降尺度结果

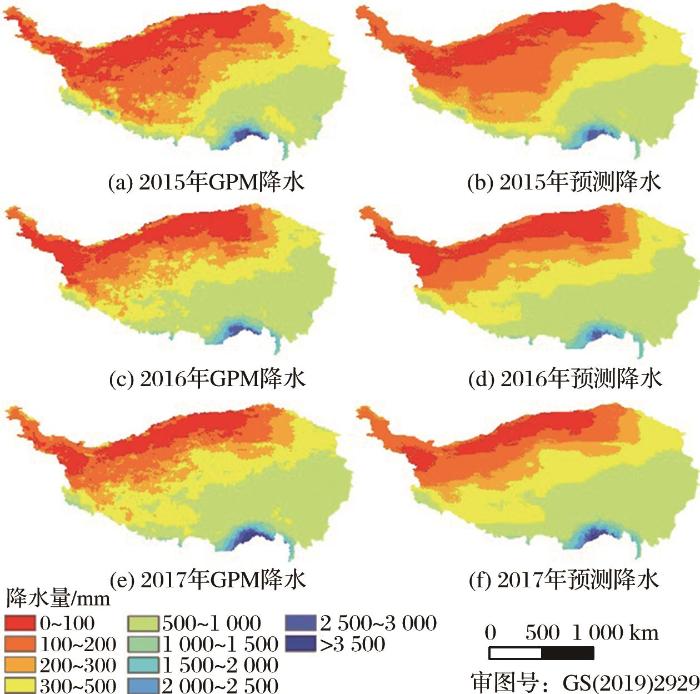
建立了降水与NDVI、高程、坡度、坡向、经度、纬度6个变量的随机森林模型，得到了2015~2017年间的年降水降尺度数据，并与GPM原始数据进行对比，如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 2015~2017年0.1°分辨率原始GPM降水数据和1 km分辨率降尺度降水数据

Fig.5 Original GPM estimates at a 0.1° resolution and downscaled annual precipitation at a 1 km resolution over the Tibetan Plateau for the years of 2015， 2016， and 2017

与原始降水数据相比，降尺度模型得到的降水数据最大值略有降低。高原西北和中北地区降水稀少，年降水量在200 mm以下，主要是因为该区域受地形阻挡作用，暖湿水汽难以到达，其中柴达木盆地由于地势低，夏季靠近高原下沉气流区，是青藏高原降水第二少的区域；东北地区略高于西边，年降水量在500 mm以下；高原中部地区年降水呈现自北向南阶梯式增长的特征，相比西北部地区降水明显增多，年降水量能到达到500 mm以上；高原东南部降水较多，特别是雅鲁藏布江的中、下游地区由于受西南季风和孟加拉湾水汽的双重影响，年降水量可以达到3 000 mm以上。从图中可以看出，模型得到的降水数据降尺度结果空间分辨率从0.1°提升到1 km，和基于GPM降水数据的累计年降水的空间分布基本一致，均体现了青藏高原地区年降水自东南向西北逐渐减少的趋势，同时存在东南部多雨区，祁连山相对多雨区，喜马拉雅山北坡少雨区的空间格局。

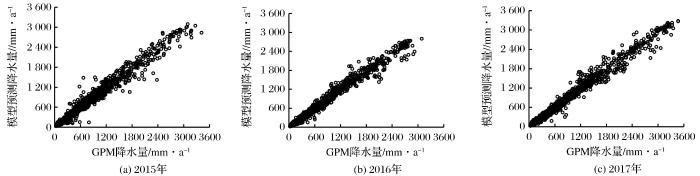
图6显示了在空间分辨率为0.1° 时利用随机森林模型预测的年降水量和GPM IMERG年累计降水数据的散点图。3年的数据均通过显著性检验（R²>0.98，P<0.0001），说明降水量与地理空间变量之间有很好的相关性。从图6也可以看出，研究区域的年降尺度降水量与原始GPM-IMERG数据一致。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 2015~2017年GPM降水数据与模型预测降尺度结果的散点图

Fig.6 Scatter plots of the agreements between the annual precipitations of the Tibetan Plateau derived from the GPM and random Forest model for the year of 2015， 2016， and 2017， respectively

4.3　月降水降尺度结果

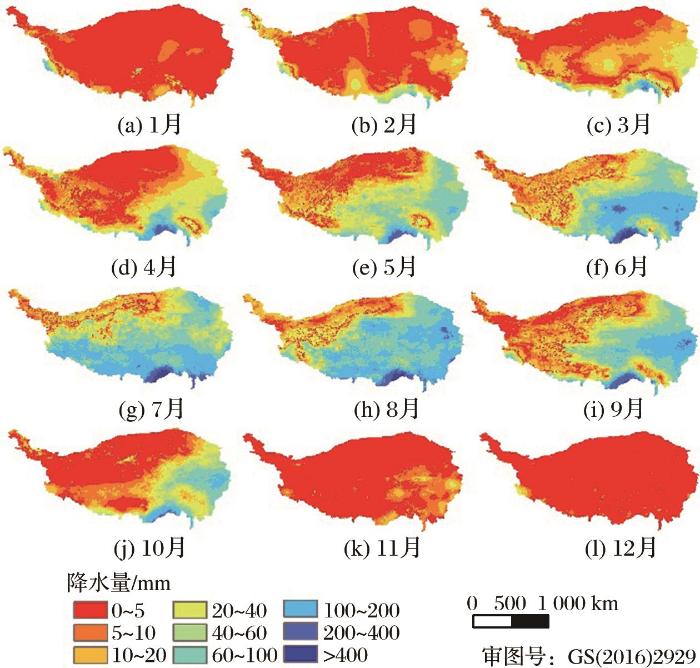
在获得的青藏高原地区的年降水降尺度数据基础上（以2017年为例），采用比例系数法分解得到1 km空间分辨率月降水。实验利用气象站点的实测数据对月估算降水数据进行校准和检验，地面站点被随机分为两组，第一组数据用于使用GDA方法校准月估算降水数据，第二组用于验证校准后的结果，校正后的月降尺度降水如图7所示。根据降尺度结果可知，降水表现出明显的阶梯状空间分布，从东南部向西北部降水逐渐降低，特别是在年降水量较大的地区，表现出降水的细节特征。青藏高原降水除具有明显的空间变异外，还具有较强的时间变异性。大部分区域的雨季从5月份开始，降雨量变大，到10月份雨季基本结束，旱季西北向东南的阶梯分布不明显。降水的时空分布与其他研究结果是一致的^{［20，31］}。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 2017年月降尺度数据

Fig.7 Downscaled precipitation at monthly scale for 2017

4.4　月降水估算结果精度评价

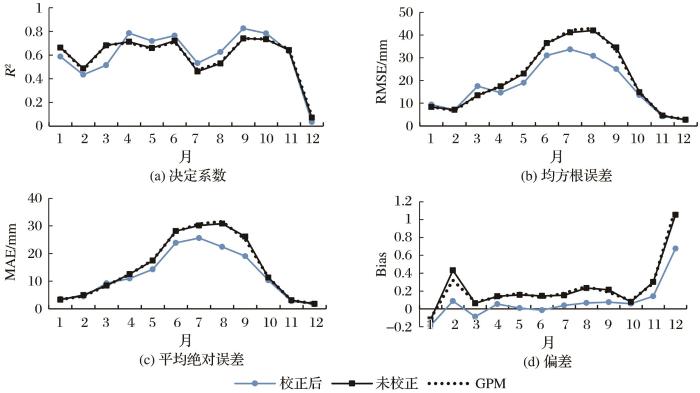
利用青藏高原地区33个雨量站的观测资料，本文采用决定系数R²、均方根误差RMSE、平均绝对误差MAE、偏差Bias验证了月降水估算结果的精度，月降水量的准确度如图8所示，月降水量的平均准确度如表2所示。从表2中可以看出，原始GPM数据与站点数据的精度总体较高（R²=0.59，RMSE=20.53 mm，MAE=14.88 mm，Bias=0.24），与未经校正的月降尺度结果的精度基本一致（R²=0.59，RMSE=20.47 mm，MAE=14.86 mm，Bias=0.24）。校正后具有较小的RMSE，MAE和Bias，R²值在校准前后变化不大，经计算ΔRMSE=-3.09 mm，ΔMAE=-2.49 mm，ΔBias=-0.16和ΔR²=0.01，这表明校正有利于提高复杂地形区模型模拟月降水精度，偏差值有明显的降低。图8显示了3年平均R²、RMSE、MAE、Bias的季节变化。R²在4~6月、9月和10月较高，其余月份较低。RMSE和MAE的月变化规律基本一致，误差值雨季高于干季，1~7月RMSE和MAE总体呈现上升趋势，8月达到峰值，9~12月下降。Bias在冬季的误差大于其他季节，冬季降水量估算不准确的一个可能原因是，NDVI值很小，对降水量不大的降水不太敏感。图8（a）~（c）还表明，与未经校准的降尺度结果相比，在大多数月份，校准方法可以提高R²、降低RMSE和MAE。图8（d）表明，校准方法显著降低了所有季节的偏差，这与已有的结果一致^［32］。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 验证站点的精度指标

Fig.8 Statistic indexes for the stations used in validation

表2 2015~2017年校正前后降尺度结果精度

Table 2 Downscaled， and calibrated precipitation data validated against data from independent rain gauge stations on the Tibetan Plateau for 2015~2017

检验指标	原始GPM	校正前	校正后
R²	0.59	0.59	0.60
RMSE/mm	20.53	20.47	17.38
MAE/mm	14.88	14.86	12.37
Bias	0.24	0.24	0.08

新窗口打开| 下载CSV

5 结论

实验对青藏高原2015~2017年的TRMM和GPM月降水产品的精度进行分析，并基于随机森林模型对GPM IMERG产品进行降尺度研究，通过分解和校正最终获取1 km分辨率月降水资料。主要结论如下：

（1）青藏高原2015~2017年GPM IMERG月降水数据与地面站点观测数据具有较高的相关性，整体上R²值为0.79， Bias值为11.75%，总体上高估了降水。对干旱和半干旱地区的GPM IMERG和TRMM 3B43进行逐月精度检验，GPM的表现优于TRMM，与实际降水更为接近。

（2）基于随机森林算法建立的降尺度模型可以极大地提高GPM IMERG降水数据在青藏高原地区的空间分辨率，并能准确地反映研究区降水的空间分布特征。

（3）通过站点校正得到的1 km月降水降尺度数据，精度具有明显的季节变化，校正后显著降低了所有季节的偏差和雨季的误差。

通过对2015~2017年的GPM IMERG降水数据进行降尺度计算，可以为青藏高原地区提供更高空间分辨率和精度的降水数据，对气候条件多样、地形复杂地区的水文气象研究具有重要的应用价值。但研究仍存在不足，首先，由于研究区站点数量较少且分布不均，在对月降水降尺度数据进行校正时引入了误差，因而降低了结果的准确度。其次，研究区的降水产品观测值的误差较大，在冬季更加明显，后续考虑引入其他对冬季降水变化敏感的因子，建立一个更可靠、更稳定的模型。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

S C

， Zhao

Z Q

， Xie

M M

， et al.

Investigating Spatial Non-stationary and Scale-dependent Relationships between Urban Surface Temperature and Environmental Factors Using Geographically Weighted Regression

［J］. Environmental Modelling & Software， 2010， 25（12）：1789-1800. doi：10.1016/j.envsoft.2010.06.011.