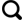1 引 言
雷达高度计作为HY-2B卫星的主载荷之一,承担海面高度、有效波高和风速的测量任务。为了保证HY-2B卫星业务化运行数据的准确性、稳定性和连续性,需要对HY-2B卫星雷达高度计进行在轨高程定标与真实性检验。
现有的星载雷达高度计大多采用超稳晶振(USO)提供时间基准。高度计发射升空后,由于器件老化等原因,超稳晶振漂移率较大,长期运行很难保证较高的频率准确度。由于高度计担负着测量全球海平面长期变化率的任务,时钟频率偏差将导致海平面变化率测量严重失真,例如,HY-2A高度计时钟偏差导致高度计测得的平均海面高度存在约40 cm/a的显著漂移[1 ] 。因此作为高程定标中的重要一环,高度计时钟偏差必须进行测量和校正。
国内外针对高度计时钟偏差估计也取得了一些成果。20世纪90年代,欧洲空间局的ERS卫星在每周飞临Kiruna地面站上空时,通过“位—同步器(bit-synchronizer)”与原子钟频标实时对比,计算出时钟频率偏差校正值[2 ] 。2004年,Lillibridge等[3 ] 通过处理Geosat高度计的两种数据产品,建立了时钟频率偏差模型,对时钟频率偏差导致的距离偏差估计精度达1 mm。2007年,Scharroo等[4 ] 基于ENVISAT卫星,利用为高度计数据提供时间基准的设备仪器控制单元时钟(ICU)对高度计时钟进行频率偏差估计和校正。在Jason-1卫星上DORIS系统通过地面站广播信号进行时间传递,可以确定星上DORIS接收机晶振的真实频率。在Jason-2卫星上,激光链路时间传输(T2L2)系统将提供对DORIS时间和频率行为的精确监测[5 ] 。2015年,万珺之等[6 ] 提出了一种基于有源定标器的高度计时钟偏差测试方法,并应用于HY-2A高度计上,首次实现了基于有源定标器的星地间在轨测试,时钟偏差测量精度优于0.1 Hz,对应的距离偏差精度优于1 mm。
HY-2B高度计是全球首个采用铷原子钟提供时间基准的雷达高度计。相较于超稳晶振,原子钟性能更高,稳定度更好,不易产生较大漂移。因原子钟频率长期稳定度很高,因此对其精度的测量有了更高的要求。针对HY-2A高度计时钟偏差估计方法进行了改进,提出了一种更优的基于有源定标器的高度计时钟偏差估计的方法,通过对比卫星与有源定标器信号单、双程路径抛物线函数的时间偏移量,避免了原方法因存在路径校正的残余误差量,致使影响时钟偏差计算结果,新方法的时钟频率偏差测量精度优于0.001 Hz。
2 在轨测试原理
若想准确测量HY-2B高度计时钟频率偏差,需利用有源定标器接收的高度计信号数据和高度计接收的有源定标器转发信号数据,通过数据处理及算法得到时钟频率偏差。因此,需首先了解有源定标器、高度计工作原理以及星地几何关系。
2.1 有源定标器工作原理
有源定标器接收来自星载雷达高度计的发射信号,对信号进行波形记录和存储,为卫星的在轨定标实验提供实测数据。同时,信号经过设定延迟后转发给星载雷达高度计。通过设置有源定标器转发信号延迟,使星载雷达高度计在处理接收信号时能够将定标器回波同地表回波分离开,便于对星载雷达高度计进行绝对高程定标测试[7 ] 。
和传统的转发体制不同,有源定标器采用了“脉冲重建”的新体制。该体制下,延时、放大和转发不再是仅仅在射频阶段中实现,而是先将射频信号经过去斜、下变频、放大、滤波、解调等环节最终生成基带的I、Q信号并进行数字处理。延时在数控单元中完成,提高了灵活性和精度。由带有高度计发射信号信息的I、Q信号生成有源定标器发射单元的I、Q信号,再经过正交调制、放大滤波、上变频等环节后,生成适当功率的线性调频信号,即等效为生成一个“回波”,发射至卫星雷达高度计[8 ] 。
2.2 高度计搜索模式
HY-2B高度计是Ku/C双频雷达高度计,Ku波段中心频率为13.58 GHz,C波段中心频率为5.25 GHz。其正常工作模式为跟踪模式,在利用有源定标器对其进行在轨定标时,高度计切换至搜索模式。卫星过境后,高度计再次切换为跟踪模式。
如图1 所示,HY-2B高度计采用时宽为102.4 μs,带宽为320 MHz的线性调频脉冲。在搜索模式下,高度计发射到发射信号的时间间隔为固定值tatt =6.782 4 ms,发射到接收信号的时间间隔也为固定值tatr =7 ms。每12个Ku波段脉冲和4个C波段脉冲组成1个脉冲串(Burst)。脉冲串内,Ku波段脉冲之间的时间间隔相等,C波段脉冲之间的时间间隔相等。接收信号时,高度计会对接收到的第1、3、5、7、9、11个Ku波段脉冲和第1、3个C波段脉冲进行抽样记录和全去斜坡处理,记录获得长度为256个样本点的I路和Q路基带时域采样信号。
图1
图1
HY-2B高度计信号结构图
Fig.1
Signal sequence diagram of HY-2B altimeter
2.3 星地几何关系
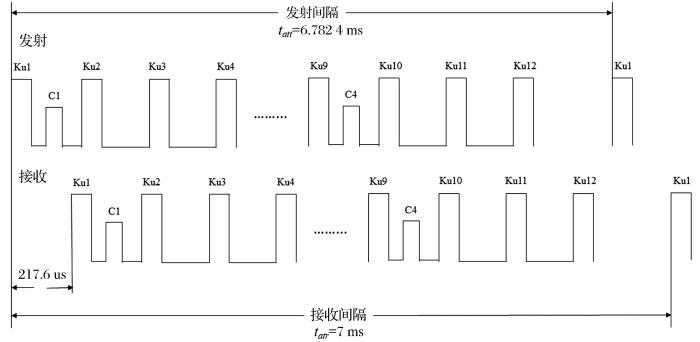
有源定标器与卫星的位置关系如图2 所示。由图2 可知,当有源定标器位置确定、卫星轨道速度和高度确定的条件下,根据余弦定理,有:
R 2 = ( R 0 + R e ) 2 + ( H + R e ) 2 - 2 ( R 0 + R e ) ( H + R e ) c o s θ (1)
图2
图2
有源定标器与卫星的几何关系图[10 ]
(H 为有源定标器相对地球参考椭球面的高度;Re 为地球半径;R 为高度计与有源定标器的相对距离;R0 为高度计到天底点高度;d 为有源定标器到卫星天底点的地表距离;θ 为距离d 对应的地心张角;v 为卫星沿轨道的速度;h 为有源定标器相对高度在卫星至天底点连线上的投影)
Fig.2
Geometric relationship between transponder and satellite
由于R=R0 -h ,对式(1)余弦函数进行泰勒级数展开并忽略二阶以上高阶小量,且有θ = d R e
c o s θ ≈ 1 - 1 2 θ 2 = 1 - 1 2 d R e 2 (2)
h = H - ( R 0 + R e ) d 2 2 R 0 R e (3)
d = v g t = R e R 0 + R e v t (4)
h = H - R e v 2 t 2 2 ( R 0 + R e ) R 0 (5)
从式(5)可以看出,有源定标器与卫星的相对距离是一个以时间t为变量的抛物线函数,称之为星地距离轨迹函数[9 ] 。
3 时钟频率偏差估计原理
高度计通过时间测量来实现距离测量。高度计发射信号的同时, 计数器开始对时钟脉冲(由高度计时钟产生且具有固定周期)计数,当高度计开始接收回波时,计数器计算从发射信号到接收回波之间,时钟共产生了多少个时钟脉冲。时钟脉冲的个数乘以单个时钟脉冲的周期,即可求出收发时间间隔,进而计算距离。若高度计时钟频率发生偏差,则将引起时钟脉冲周期发生变化,进而导致时间测量发生偏差,因此高度计时钟频率偏差导致的时间偏差称为高度计时钟偏差。
3.1 时钟频率偏差估计方法
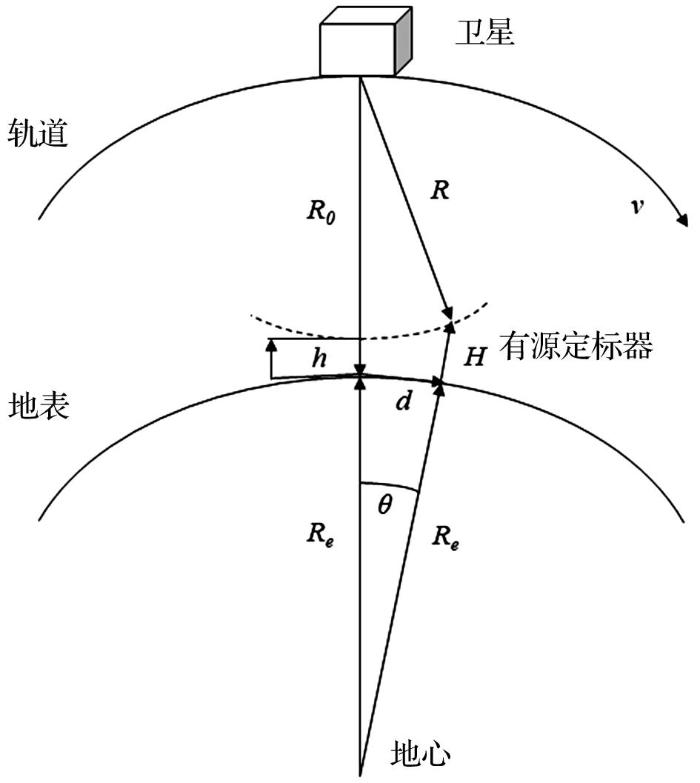
如图3 所示,高度计搜索模式下以固定时间间隔(tatt =6.782 4 ms)发射信号,因星地间相对运动和时钟偏差的存在,有源定标器接收信号的时间间隔并不固定。通过有源定标器接收信号到达时刻的差分序列,反推星地单程距离轨迹函数,时钟偏差存在于函数的一次项中。高度计每隔7 ms(tatr )主动接收一次有源定标器的重建信号,从高度计数据中得到的星地双程距离轨迹函数,时钟偏差已转换为测距偏差存在于常数项中。
图3
图3
卫星收发关系示意图
Fig.3
Schematic diagram of satellite receiving and transmitting relationship
在基于有源定标器的HY-2A高度计时钟偏差估计方法中[6 ] ,该方法在星地距离抛物线常数项中解算时钟偏差,由于其抛物线常数项中还包含了其他数项修正量所带来的误差,这使得解算过程较为繁琐,若其他误差修正不准,则残余误差会贡献到时钟偏差估计中,直接影响测量精度。本方法基于其不足之处进行改进与创新,在星地距离抛物线一次项中解算时钟偏差。
由2.3节可知,星载雷达高度计与有源定标器的相对距离是一个以时间t为变量的抛物线函数,因此可以用最简单的抛物线函数y=at2 进行建模求解时钟偏差。
假设高度计不存在时钟偏差,设高度计发射—发射信号的单程距离R 0 ( t )
R 0 ( t ) = a t 2 (6)
R 1 ( t ) = a ( t + t a t r ) 2 (7)
R ( t ) = a t 2 + a ( t + t a t r ) 2 = 2 a ( t + t a t r 2 ) 2 + t a t r 2 4 (8)
由式(6)与式(8)可知,在没有时钟偏差的情况下,高度计发射—发射信号的单程距离抛物线顶点与高度计发射—接收信号的双程距离抛物线顶点相差t a t r 2
R 0 ( t ) = a ( t + Δ T a ) 2 (9)
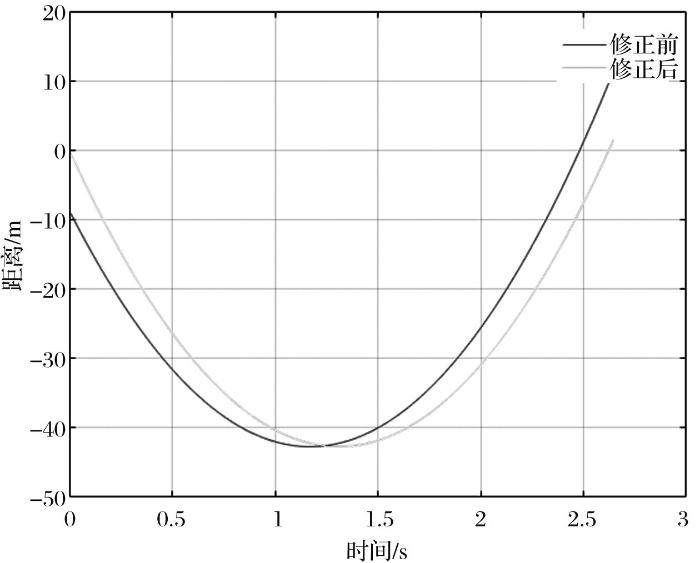
由式(9)可知,高度计时钟偏差将导致高度计发射—发射信号的单程距离抛物线顶点发生偏移(图4 )。
图4
图4
修正钟差前后有源定标器反演单程距离抛物线顶点对比
Fig.4
Comparison of one-way distance parabola vertex inversion by transponder before and after correction of clock bias
R 0 ' ( t ) = 2 a ( t + Δ T a ) (10)
由上式可知,含有时钟偏差的高度计发射—发射信号差分序列是一个截距为2 a Δ T a Δ T a 0
Δ T a 0 = 2 a Δ T a [ Δ T a T a 0 ] (11)
其中:2 a Δ T a T a 0
由此得到的单个脉冲的时间偏差可以推导出HY-2B高度计时钟的频率偏差Δ f a t o
Δ f a t o = 1 T a 0 + Δ T a 0 - f a t o (12)
其中:fato =1/Ta0 为HY-2B高度计时钟的标称频率80 MHz。
3.2 修正多普勒误差
星载雷达高度计与有源定标器存在相对运动,因此高度计与有源定标器接收的信号中均包含多普勒频移导致的误差。有源定标器接收信号中存在的频率偏差f a
f a = - v a λ (13)
f b = - v b λ (14)
其中:λ va 、vb 为星地间径向运动速度,由于HY-2B高度计在搜索模式下接收信号时间间隔固定,星地间径向运动速度可以用高度计相邻接收信号时刻的星地距离变化率来近似表示,因此,在t时刻,有源定标器接收信号中由多普勒频移引入的测距偏差为:
D o p t r ( t ) = - K R 2 ( t ) - R 0 ( t ) t a t t (15)
D o p a l t ( t ) = - K R 3 ( t ) - R 1 ( t ) t a t t (16)
K = 5.25 G H z × 102.4 μ s 320 M H z = 0.001 68 s (17)
K = 13.58 G H z × 102.4 μ s 320 M H z = 0.004 345 6 s (18)
由此可知,有源定标器时间差分序列中包含多普勒误差。因HY-2A高度计时钟采用超稳晶振,在时钟频率偏差动辄数十赫兹的情况下,多普勒误差对其影响几乎可以忽略不计,这与HY-2B有很大不同。由于HY-2B高度计时钟频率偏差极小,有源定标器时间差分序列中存在多普勒误差将对时钟频率偏差估计产生重要影响,因此,修正多普勒误差是高度计时钟频率偏差估计的前提。
3.3 其他误差源分析
有源定标器采用铷原子钟提供时钟频率,其频率为80 MHz,周期为12.5 ns,与HY-2B高度计时钟参数完全一致。实验前已将有源定标器时钟进行校准,因此可以视为参考时钟。
有源定标器可以自由设定转发延迟,以便与地表回波进行区分。同时,有源定标器系统内部存在固有硬件延迟,为了给定标提供一个绝对的延时和衰减基准,每台有源定标器在实验开始前需进行一次自定标。
信号在有源定标器与高度计间传输,会产生路径延迟,主要包括干、湿对流层延迟和电离层延迟。在定标实验中,有源定标器天线采用天顶指向,高度计卫星过顶时间仅有3 s左右,考虑到高度计跟踪窗的有限长度(120 m)和有源定标器天线较窄的波束宽度(<1°),可以认为在定标过程中,干、湿对流层延迟和电离层延迟均为定值[11 ] 。
高度计的测量值应是指高度计天线相位中心到测量目标之间的直线几何距离,然而这个测量值实际是信号从发射机到接收机的全部路径。信号在高度计内部传输距离就构成了高度计系统延迟。
由式(6)与式(8)可知,计算高度计时钟偏差仅与星地距离抛物线顶点有关。而上述延迟所带来的误差在一次定标实验中均可以视为常数,并不会对抛物线顶点产生影响。因此,相较于基于有源定标器的HY-2A雷达高度计时钟偏差估计的方法[6 ] ,本方法有效避免了信号传输过程中各项修正量所带来的误差。
4 测试结果
自2019年4月23日至11月5日共进行了9次基于有源定标器HY-2B高度计时钟频率偏差在轨测试,测试结果如表1 所示。
根据表1 的频率偏差测量结果可以得到,时钟频率偏差绝对值不超过0.1 Hz。Ku波段的频率偏差标准差为6.76×10-4 Hz,C波段的频率偏差标准差为1.66×10-4 Hz,证明新方法的时钟频率偏差测量精度优于0.001 Hz。
HY-2B雷达高度计原子钟标称频率为80 MHz,标称频率准确度为±5×10-10 。频率准确度A是指实际频率与标称频率的一致程度[12 ] 。采用如下公式表达:
A = Δ f a t o f a t o
图5
图5
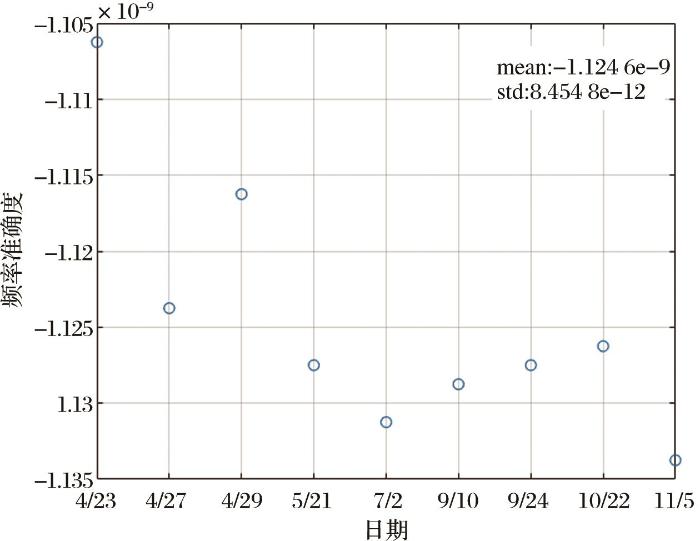
HY-2B高度计原子钟频率准确度测量结果
Fig.5
Measurement results of frequency accuracy of atomic clock of HY-2B altimeter
由图5 可以看出在有源定标器的测量能力下,原子钟频率准确度为-1.1246×10-9 。根据式(20)计算时钟最大漂移率。
Q = Δ f a t o ( m a x ) - Δ f a t o ( m i n ) D
其中:Δfato (max)为最大频率偏差,Δfato (min)为最小频率偏差,D 为间隔天数。因此时钟最大漂移率Q 为-1.122 4×10-5 Hz/d,导致的最大测距漂移率为Q ×C=2.946 1×10-7 m/d。因频率漂移所带来的误差对测距的影响微乎其微,表明HY-2B高度计原子钟性能稳定。
5 结 论
针对HY-2A高度计时钟偏差估计方法进行了改进,提出了从星地斜距函数曲线时间偏移量中提取高度计时钟偏差的估计方法。通过有源定标器接收高度计搜索模式下的发射信号和高度计接收到的有源定标器的转发信号,获取了星地信号路径抛物线函数。将时钟偏差估计转换到对抛物线函数顶点的解析上,有效避免路径延迟等其他误差的影响。在轨测试结果表明,HY-2B雷达高度计原子钟稳定、准确,为后续的高度计系统延迟定标提供了时钟基准。
参考文献
View Option
[1]
Raynal M HY-2A: Global Statistical Assessment and Cross-calibration with Jason-2 over Ocean
[R]. FRANCE : Collecte Localisation Satellites (CLS) , 2014 .
[本文引用: 1]
[2]
Anzenhofer M Gruber T Fully Reprocessed ERS-1 Altimeter Data from 1992 to 1995: Feasibility of the Detection of Long Term Sea Level Change
[J]. Journal of Geophysical Research Atmospheres , 1998 , 103 (C4 ):8089 –8112 .doi:10.1029/97JC02566 .
[本文引用: 1]
[3]
Lillibridge J Smith W Scharroo R et al The Geosat Geodetic Mission Twentieth Anniversary Edition Data Product
[C]∥ AGU Fall Meeting Abstracts . USA : American Geophysical Union , 2004 ,1 :786 .
[本文引用: 1]
[4]
Scharroo R Faugère Y Roca M et al Envisat RA-2 USO Anomaly: Impact and Correction
[C]∥ 2007 Envisat Symposium , Eur. Space Agency Spec. Publ.ESA SP- 636 .2007 .
[本文引用: 1]
[5]
Jayles C Nhun-Fat B Tourain C DORIS: System Description and Control of the Signal Integrity
[J]. Journal of Geodesy ,2006 ,80 (8-11 ):457 -472 .doi:10.1007/s00190-006-0046-8 .
[本文引用: 1]
[6]
Wan J Z Guo W Zhao F et al HY-2A Radar Altimeter Ultrastable Oscillator Drift Estimation Using Reconstructive Transponder with Its Validation by Multimission Cross Calibration
[J]. IEEE Transactions on Geoscience and Remote Sensing ,2015 ,53 (9 ):5229 -5236 . doi:10.1109/TGRS.2015. 2419670 .
[本文引用: 3]
[7]
Gong Xunwu Guo Wei Wan Junzhi Study on the Approach for Backscattering Coefficient In-orbit Calibration of HY-2 Altimeter Using A Reconstructive Transponder
[J].Remote Sensing Technology and Application ,2017 ,32 (2 ):374 -379 .
[本文引用: 1]
龚循武 ,郭伟 ,万珺之 基于有源定标器的 HY-2高度计后向散射系数在轨定标方法研究
[J]. 遥感技术与应用 ,2017 ,32 (2 ):374 -379 .
[本文引用: 1]
[8]
Wang C Y Guo W Zhao F et al Development of the Reconstructive Transponder for In-Orbit Calibration of HY-2A Altimeter
[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing , 2015 , 9 (6 ):2709 -2719 . doi:10.1109/JSTARS.2016.2544759 .
[本文引用: 1]
[9]
Gong Xiaoyan Development of Digital Control Unit of the Transponder for HY-2 Altimeter
[D].Beijing : University of Chinese Academy of Sciences ,2012 .
[本文引用: 1]
宫小艳 HY-2高度计有源定标器数控单元研制
[D].北京 :中国科学院大学 ,2012 .
[本文引用: 1]
[10]
Mathews M B Design, Testing, and Performance Analysis of Transponders for Use with Satellite Altimeters
.[D]. Boulder , the USA: University of Colorado , 1995 .
[本文引用: 1]
[11]
Wan Junzhi Research on the Absolute Calibration of the Ocean 2 Altimeter System based on Transponder
[D].Beijing : University of Chinese Academy of Sciences ,2015 .万珺之.基于有源定标器的海洋二号高度计系统延迟在轨绝对定标研究[D].北京:中国科学院大学 ,2015.
[本文引用: 1]
[12]
Jia Xiaolin Feng Laiping Mao Yue et al Performance Evalution of GPS On-borad Clock
[J]. Journal of Time and Frequency ,2010 ,33 (2 ):115 -120 .
[本文引用: 1]
贾小林 ,冯来平 ,毛悦 ,等 GPS星载原子钟性能评估
[J].时间频率学报 ,2010 ,33 (2 ):115 -120 .
[本文引用: 1]
HY-2A: Global Statistical Assessment and Cross-calibration with Jason-2 over Ocean
1
2014
... 现有的星载雷达高度计大多采用超稳晶振(USO)提供时间基准.高度计发射升空后,由于器件老化等原因,超稳晶振漂移率较大,长期运行很难保证较高的频率准确度.由于高度计担负着测量全球海平面长期变化率的任务,时钟频率偏差将导致海平面变化率测量严重失真,例如,HY-2A高度计时钟偏差导致高度计测得的平均海面高度存在约40 cm/a的显著漂移[1 ] .因此作为高程定标中的重要一环,高度计时钟偏差必须进行测量和校正. ...
Fully Reprocessed ERS-1 Altimeter Data from 1992 to 1995: Feasibility of the Detection of Long Term Sea Level Change
1
1998
... 国内外针对高度计时钟偏差估计也取得了一些成果.20世纪90年代,欧洲空间局的ERS卫星在每周飞临Kiruna地面站上空时,通过“位—同步器(bit-synchronizer)”与原子钟频标实时对比,计算出时钟频率偏差校正值[2 ] .2004年,Lillibridge等[3 ] 通过处理Geosat高度计的两种数据产品,建立了时钟频率偏差模型,对时钟频率偏差导致的距离偏差估计精度达1 mm.2007年,Scharroo等[4 ] 基于ENVISAT卫星,利用为高度计数据提供时间基准的设备仪器控制单元时钟(ICU)对高度计时钟进行频率偏差估计和校正.在Jason-1卫星上DORIS系统通过地面站广播信号进行时间传递,可以确定星上DORIS接收机晶振的真实频率.在Jason-2卫星上,激光链路时间传输(T2L2)系统将提供对DORIS时间和频率行为的精确监测[5 ] .2015年,万珺之等[6 ] 提出了一种基于有源定标器的高度计时钟偏差测试方法,并应用于HY-2A高度计上,首次实现了基于有源定标器的星地间在轨测试,时钟偏差测量精度优于0.1 Hz,对应的距离偏差精度优于1 mm. ...
The Geosat Geodetic Mission Twentieth Anniversary Edition Data Product
1
2004
... 国内外针对高度计时钟偏差估计也取得了一些成果.20世纪90年代,欧洲空间局的ERS卫星在每周飞临Kiruna地面站上空时,通过“位—同步器(bit-synchronizer)”与原子钟频标实时对比,计算出时钟频率偏差校正值[2 ] .2004年,Lillibridge等[3 ] 通过处理Geosat高度计的两种数据产品,建立了时钟频率偏差模型,对时钟频率偏差导致的距离偏差估计精度达1 mm.2007年,Scharroo等[4 ] 基于ENVISAT卫星,利用为高度计数据提供时间基准的设备仪器控制单元时钟(ICU)对高度计时钟进行频率偏差估计和校正.在Jason-1卫星上DORIS系统通过地面站广播信号进行时间传递,可以确定星上DORIS接收机晶振的真实频率.在Jason-2卫星上,激光链路时间传输(T2L2)系统将提供对DORIS时间和频率行为的精确监测[5 ] .2015年,万珺之等[6 ] 提出了一种基于有源定标器的高度计时钟偏差测试方法,并应用于HY-2A高度计上,首次实现了基于有源定标器的星地间在轨测试,时钟偏差测量精度优于0.1 Hz,对应的距离偏差精度优于1 mm. ...
Envisat RA-2 USO Anomaly: Impact and Correction
1
636
... 国内外针对高度计时钟偏差估计也取得了一些成果.20世纪90年代,欧洲空间局的ERS卫星在每周飞临Kiruna地面站上空时,通过“位—同步器(bit-synchronizer)”与原子钟频标实时对比,计算出时钟频率偏差校正值[2 ] .2004年,Lillibridge等[3 ] 通过处理Geosat高度计的两种数据产品,建立了时钟频率偏差模型,对时钟频率偏差导致的距离偏差估计精度达1 mm.2007年,Scharroo等[4 ] 基于ENVISAT卫星,利用为高度计数据提供时间基准的设备仪器控制单元时钟(ICU)对高度计时钟进行频率偏差估计和校正.在Jason-1卫星上DORIS系统通过地面站广播信号进行时间传递,可以确定星上DORIS接收机晶振的真实频率.在Jason-2卫星上,激光链路时间传输(T2L2)系统将提供对DORIS时间和频率行为的精确监测[5 ] .2015年,万珺之等[6 ] 提出了一种基于有源定标器的高度计时钟偏差测试方法,并应用于HY-2A高度计上,首次实现了基于有源定标器的星地间在轨测试,时钟偏差测量精度优于0.1 Hz,对应的距离偏差精度优于1 mm. ...
DORIS: System Description and Control of the Signal Integrity
1
2006
... 国内外针对高度计时钟偏差估计也取得了一些成果.20世纪90年代,欧洲空间局的ERS卫星在每周飞临Kiruna地面站上空时,通过“位—同步器(bit-synchronizer)”与原子钟频标实时对比,计算出时钟频率偏差校正值[2 ] .2004年,Lillibridge等[3 ] 通过处理Geosat高度计的两种数据产品,建立了时钟频率偏差模型,对时钟频率偏差导致的距离偏差估计精度达1 mm.2007年,Scharroo等[4 ] 基于ENVISAT卫星,利用为高度计数据提供时间基准的设备仪器控制单元时钟(ICU)对高度计时钟进行频率偏差估计和校正.在Jason-1卫星上DORIS系统通过地面站广播信号进行时间传递,可以确定星上DORIS接收机晶振的真实频率.在Jason-2卫星上,激光链路时间传输(T2L2)系统将提供对DORIS时间和频率行为的精确监测[5 ] .2015年,万珺之等[6 ] 提出了一种基于有源定标器的高度计时钟偏差测试方法,并应用于HY-2A高度计上,首次实现了基于有源定标器的星地间在轨测试,时钟偏差测量精度优于0.1 Hz,对应的距离偏差精度优于1 mm. ...
HY-2A Radar Altimeter Ultrastable Oscillator Drift Estimation Using Reconstructive Transponder with Its Validation by Multimission Cross Calibration
3
2015
... 国内外针对高度计时钟偏差估计也取得了一些成果.20世纪90年代,欧洲空间局的ERS卫星在每周飞临Kiruna地面站上空时,通过“位—同步器(bit-synchronizer)”与原子钟频标实时对比,计算出时钟频率偏差校正值[2 ] .2004年,Lillibridge等[3 ] 通过处理Geosat高度计的两种数据产品,建立了时钟频率偏差模型,对时钟频率偏差导致的距离偏差估计精度达1 mm.2007年,Scharroo等[4 ] 基于ENVISAT卫星,利用为高度计数据提供时间基准的设备仪器控制单元时钟(ICU)对高度计时钟进行频率偏差估计和校正.在Jason-1卫星上DORIS系统通过地面站广播信号进行时间传递,可以确定星上DORIS接收机晶振的真实频率.在Jason-2卫星上,激光链路时间传输(T2L2)系统将提供对DORIS时间和频率行为的精确监测[5 ] .2015年,万珺之等[6 ] 提出了一种基于有源定标器的高度计时钟偏差测试方法,并应用于HY-2A高度计上,首次实现了基于有源定标器的星地间在轨测试,时钟偏差测量精度优于0.1 Hz,对应的距离偏差精度优于1 mm. ...
... 在基于有源定标器的HY-2A高度计时钟偏差估计方法中[6 ] ,该方法在星地距离抛物线常数项中解算时钟偏差,由于其抛物线常数项中还包含了其他数项修正量所带来的误差,这使得解算过程较为繁琐,若其他误差修正不准,则残余误差会贡献到时钟偏差估计中,直接影响测量精度.本方法基于其不足之处进行改进与创新,在星地距离抛物线一次项中解算时钟偏差. ...
... 由式(6) 与式(8) 可知,计算高度计时钟偏差仅与星地距离抛物线顶点有关.而上述延迟所带来的误差在一次定标实验中均可以视为常数,并不会对抛物线顶点产生影响.因此,相较于基于有源定标器的HY-2A雷达高度计时钟偏差估计的方法[6 ] ,本方法有效避免了信号传输过程中各项修正量所带来的误差. ...
基于有源定标器的 HY-2高度计后向散射系数在轨定标方法研究
1
2017
... 有源定标器接收来自星载雷达高度计的发射信号,对信号进行波形记录和存储,为卫星的在轨定标实验提供实测数据.同时,信号经过设定延迟后转发给星载雷达高度计.通过设置有源定标器转发信号延迟,使星载雷达高度计在处理接收信号时能够将定标器回波同地表回波分离开,便于对星载雷达高度计进行绝对高程定标测试[7 ] . ...
基于有源定标器的 HY-2高度计后向散射系数在轨定标方法研究
1
2017
... 有源定标器接收来自星载雷达高度计的发射信号,对信号进行波形记录和存储,为卫星的在轨定标实验提供实测数据.同时,信号经过设定延迟后转发给星载雷达高度计.通过设置有源定标器转发信号延迟,使星载雷达高度计在处理接收信号时能够将定标器回波同地表回波分离开,便于对星载雷达高度计进行绝对高程定标测试[7 ] . ...
Development of the Reconstructive Transponder for In-Orbit Calibration of HY-2A Altimeter
1
2015
... 和传统的转发体制不同,有源定标器采用了“脉冲重建”的新体制.该体制下,延时、放大和转发不再是仅仅在射频阶段中实现,而是先将射频信号经过去斜、下变频、放大、滤波、解调等环节最终生成基带的I、Q信号并进行数字处理.延时在数控单元中完成,提高了灵活性和精度.由带有高度计发射信号信息的I、Q信号生成有源定标器发射单元的I、Q信号,再经过正交调制、放大滤波、上变频等环节后,生成适当功率的线性调频信号,即等效为生成一个“回波”,发射至卫星雷达高度计[8 ] . ...
HY-2高度计有源定标器数控单元研制
1
2012
... 从式(5) 可以看出,有源定标器与卫星的相对距离是一个以时间t为变量的抛物线函数,称之为星地距离轨迹函数[9 ] . ...
HY-2高度计有源定标器数控单元研制
1
2012
... 从式(5) 可以看出,有源定标器与卫星的相对距离是一个以时间t为变量的抛物线函数,称之为星地距离轨迹函数[9 ] . ...
Design, Testing, and Performance Analysis of Transponders for Use with Satellite Altimeters
1
1995
... 有源定标器与卫星的位置关系如
图2 所示.由
图2 可知,当有源定标器位置确定、卫星轨道速度和高度确定的条件下,根据余弦定理,有:
R 2 = ( R 0 + R e ) 2 + ( H + R e ) 2 - 2 ( R 0 + R e ) ( H + R e ) c o s θ (1) 图2 有源定标器与卫星的几何关系图<sup>[<xref ref-type="bibr" rid="R10">10</xref>]</sup> (H 为有源定标器相对地球参考椭球面的高度;Re 为地球半径;R 为高度计与有源定标器的相对距离;R0 为高度计到天底点高度;d 为有源定标器到卫星天底点的地表距离;θ 为距离d 对应的地心张角;v 为卫星沿轨道的速度;h 为有源定标器相对高度在卫星至天底点连线上的投影) ...
Research on the Absolute Calibration of the Ocean 2 Altimeter System based on Transponder
1
2015
... 信号在有源定标器与高度计间传输,会产生路径延迟,主要包括干、湿对流层延迟和电离层延迟.在定标实验中,有源定标器天线采用天顶指向,高度计卫星过顶时间仅有3 s左右,考虑到高度计跟踪窗的有限长度(120 m)和有源定标器天线较窄的波束宽度(<1°),可以认为在定标过程中,干、湿对流层延迟和电离层延迟均为定值[11 ] . ...
GPS星载原子钟性能评估
1
2010
... HY-2B雷达高度计原子钟标称频率为80 MHz,标称频率准确度为±5×10-10 .频率准确度A是指实际频率与标称频率的一致程度[12 ] .采用如下公式表达: ...
GPS星载原子钟性能评估
1
2010
... HY-2B雷达高度计原子钟标称频率为80 MHz,标称频率准确度为±5×10-10 .频率准确度A是指实际频率与标称频率的一致程度[12 ] .采用如下公式表达: ...