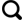1 引言
重力反演与气象实验卫星(Gravity Recovery and Climate Experiment,GRACE)发射于2002年3月,主要任务是对地球重力场的时空变化进行精准测量,在陆地区域,月尺度上的重力场变化反映的主要是水储量变化,因此GRACE数据也常用来计算水储量变化[9]。然而,受到观测方式、传感器等因素的影响,GRACE数据中主要存在两类误差[10]。一类是重力场误差,GRACE数据以球谐系数的形式提供给用户使用,而在高阶项球谐系数中存在明显的重力场误差,并随着球谐系数阶数的增加而增加。为了抑制重力场误差,计算水储量时,往往会截取球谐系数。然而,球谐系数保留阶数越少,GRACE数据空间分辨率就越低[11],因此常截取前60阶球谐系数进行计算[12]。即便如此,保留的高阶系数中仍存在显著误差。这一误差常用高斯滤波进行处理[10],通过比例因子降低高阶项权重实现噪声抑制。另一类误差是南北方向上的条带噪声,由于GRACE观测的是南北方向上两颗轨道卫星间的距离变化,因此最终计算结果中会存在明显的南北条带噪声。Swenson等[13]发现条带噪声主要由球谐系数中系统性的相关误差引起,提出利用滑动窗口分别对奇(偶)数阶球谐系数间存在的相关性误差进行消除。综上,目前对于卫星数据噪声的处理,常用的方法是球谐系数截取、去相关滤波以及高斯滤波的组合。
近年来,已有学者结合多源水文数据进行水储量变化研究[7,16,17]。Döll等[16]结合GHMs模型数据与GRACE观测数据计算了地下水衰减速率,并使用监测水井进行验证,结果表明两者具有良好的一致性,这说明GHMs模型与GRACE数据的结合使用能更好地分析水储量变化。国内学者龙笛等[17]分析了GRACE水储量变化与降水、气温等气象数据间的相关性,并利用人工神经网络建立水储量变化与这些气象数据之间的统计回归关系,重建了1980年至2002年水储量变化历史数据。冯贵平等[18]从GRACE计算的总储水量中扣除LSMs提供的地表水、冰雪等辅助数据得到全球地下水储量时间序列,并对其季节性和长期变化特征进行了分析。此外,龙笛等利用三角帽法在流域尺度对GRACE、LSMs与GHMs三类数据产品进行不确定性分析,在此基础上以全球水文模型WGHM数据为参考,使用贝叶斯模型平均方法对GRACE数据进行融合处理[7],结果表明结合多源数据优势能提升卫星观测数据精度。但该方法融合过程中权值参数的确定较大程度上依赖于参考数据的选取,而不同数据产品在不同区域甚至不同像素位置的精度差异较大,在流域尺度利用单一产品为参考估算权值可能引入较大误差。
基于上述分析,实验拟结合GRACE、全球水文模型(GHMs)以及陆面模型(LSMs)数据,引入点面融合思想,利用GRACE数据和模型模拟数据互相约束选取训练点,基于BP神经网络、深度置信网络建立校正模型,对GRACE月尺度数据进行精度校正,降低数据不确定性,实现质量提升。
2 数据与处理
2.1 GRACE数据
目前GRACE数据主要由美国德克萨斯大学空间中心(Center for Space Research,CSR)、美国宇航局喷气推进实验室(Jet Propulsion Laboratory,JPL)和德国地学研究中心(German Research Center for Geoscience,GFZ)以球谐系数的形式提供。后文中根据数据的处理机构,以CSR、JPL和GFZ缩写对数据产品进行区分。本文使用的是Level-3级数据,它是在RL05版球谐系数基础上经过后处理(60阶次系数截取、去相关、高斯滤波)以及信号恢复得到的陆地栅格数据,空间分辨率为1°×1°。时间分辨率以月为单位,实验中使用了 2003年3月至2012年9月,共 111 期数据(数据下载地址:
2.2 陆面模型
陆面模型是针对发生在大气、地表和土壤层之间的能量、水分交互过程建立起来的计算机模型,该模型基于不同的物理机制对各个过程进行参数化处理,从而实现对陆面过程的研究分析。常用的有CLM(Community Land Model)、Mosaic、Noah三个陆面过程模型以及VIC(Variable Infiltration Capacity)水文模型,如表1所示。实验使用的4类LSMs模型同化数据来自于全球陆面同化系统(Global Land Data Assimilation System ,GLDAS),该系统由美国国家航空航天局(National Aeronautics and Space Administration,NASA)和国家海洋与大气管理局(National Oceanic and Atmospheric Administration ,NOAA)共同开发,并以卫星遥感观测和地表站点数据作为驱动数据,调用对应的陆面模型,最终得到近地面气温、降水量、雪水当量、冠层水以及土壤含水量等数据,产品发布于
表1 陆面模型介绍
Table 1
| 模型名称 | 研究机构 | 空间分辨率 | 土壤层数量 | 土壤层深度/m |
|---|---|---|---|---|
| CLM | 美国国家大气研究中心 | 1°×1° | 10 | 3.4 |
| Mosaic | 美国国家航空 航天局 | 1°×1° | 3 | 1.9 |
| Noah | 美国国家海洋与 大气管理局 | 0.25°×0.25° | 4 | 3.5 |
| VIC | 华盛顿大学 | 1°×1° | 3 | 3.5 |
2.3 全球水文模型
PCR-GLOBWB[20]模型是由荷兰乌得勒支大学开发的一款基于网格的全球水文模型,覆盖了除格陵兰岛和南极洲以外的所有大陆。模型以网格为单位模拟了大气、地表以及地下之间的水文循环过程,其中包括降水、地表径流、土壤蒸发以及植物蒸腾作用,同时也考虑了积雪,融雪和冰川融化过程。
WGHM[21]模型(WaterGAP Global Hydrology Model)是由德国法兰克福大学提供的全球水资源分析和预测模型。该模型不仅计算了各个国家或流域的长期平均水资源,还模拟了除冰川以外的所有陆地水储量组成部分,包括土壤水、径流、地下水补给、地表积雪和地表水储量变化。
2.4 地下水井水位监测数据
由于真实总水储量参考数据难以获取,本文使用地下水位数据定量评价不同水储量产品地下水分量的精度。为了保证评价结果在时间空间尺度的连续性,研究采用由美国地质勘探局(United States Geological Survey,USGS)公开提供(
2.5 数据分类与预处理
研究将水储量数据分为三大类,分别为GRACE信号恢复Level-3级产品(包括CSR、JPL、和GFZ三种);LSMs模型产品(包括Noah、VIC、CLM、Mosaic四种);GHMs模型产品(包括WGHM、PCR_GLOBWB两种),产品信息及分类结果如表2所示。
表2 水储量数据分类
Table 2
| 数据名 | 空间分辨率 | 数据类型 |
|---|---|---|
| CSR | 1°×1° | GRACE 观测数据 |
| JPL | 1°×1° | |
| GFZ | 1°×1° | |
| NOAH025_M_2.1 | 0.25°×0.25° | 陆面模型 同化数据 |
| VIC10_M_001 | 1°×1° | |
| MOS10_M_001 | 1°×1° | |
| CLM10_M_001 | 1°×1° | |
| WGHM 2.2 | 0.5°×0.5° | 全球水文模型数据 |
| PCR-GLOBWB 2 | 0.5°×0.5° |
研究所使用的所有水储量数据时间分辨率均为月尺度。为了使数据在空间分辨率上保持一致,本文实验先对Noah、WGHM以及PCR-GLOBWB模型首先进行了空间取平均操作,将空间分辨率统一采样为1°×1°。
3 计算原理与方法
3.1 研究方法
研究流程如图1所示,主要包括水储量数据不确定性分析、GRACE参考观测值选取、校正模型构建以及结果精度验证。
图1
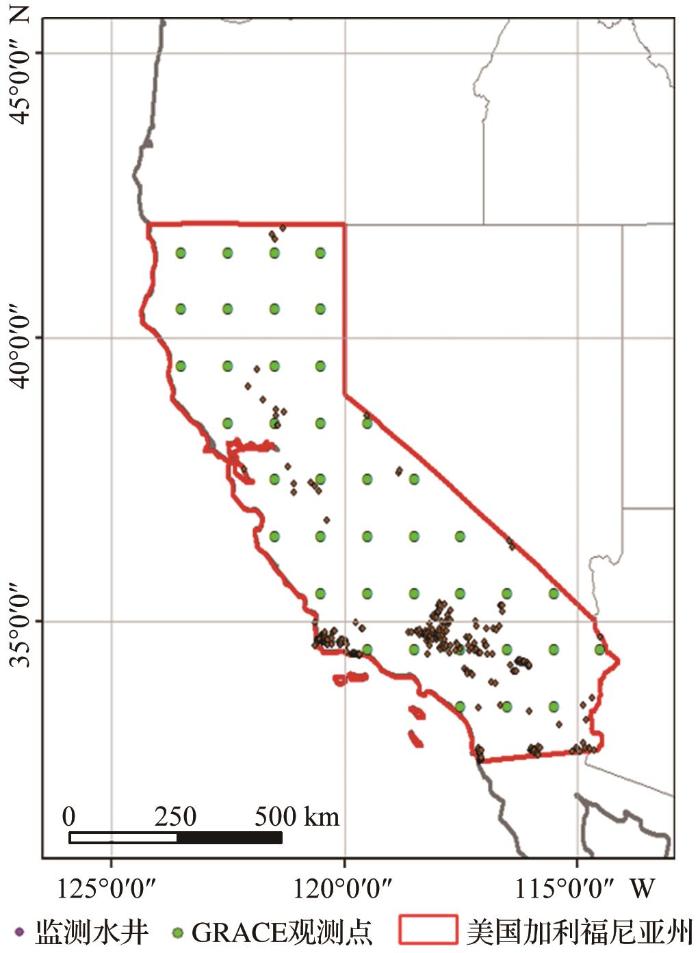
实验第一步利用三角帽方法对各类水储量数据进行不确定性分析,并逐月从GRACE以及GHMs数据中各选取不确定性最低的数据参与精度校正。第二步则基于不确定性分析结果,利用卫星观测和模型模拟数据互相约束来选取用于训练的参考值。由于部分LSMs模型缺少地下水分量,所以实验中通过设定阈值,对比不确定性最低的GRACE和GHMs水储量产品,从GRACE数据中选取参考值。第三步是根据参考值与其对应位置上的气象、水文等辅助数据建立训练集,基于BP、DBN神经网络构建GRACE校正模型,再通过训练得到的模型对剩余空间位置进行校正,其中辅助数据由LSMs模型提供。考虑到地下水井的空间分布,本研究以美国加利福尼亚州为研究区域。由于GRACE分辨率较低,为1°×1°,在加州区域内的观测值数量比较有限,输入模型进行训练时,容易出现过拟合问题,因此本研究在北美洲尺度上进行模型训练。最后对实验结果进行精度评价。具体的实验过程将在3.2~3.5节详细说明。
3.2 基于三角帽方法的不确定性评估
三角帽方法假设单次观测值由真实值与误差两部分组成,同时误差符合正态分布规律:
该差异的方差为:
假设误差
由于LSMs与GHMs模型具有相似的输入数据,因此在使用三角帽方法进行分析时,需要考虑两两数据值之间的相关性[24],即考虑
实验中使用了3类水储量数据,如表2所示。因此在单位时间(月)上每次会从GRACE、LSMs以及GHMs模型中分别选取一种数据作为输入数据进行不确定性分析,例如从GRACE数据中选出CSR,从LSMs中选出Noah,从GHMs中选出WGHM,然后将CSR、Noah以及WGHM作为输入,得到这3类产品在此次比较中的不确定性分析结果。以此类推,在通过所有组合形式的比较之后,每类产品都会得到一组不确定性分析结果,本文使用这组结果的中位数来表示该数据在当前月份的不确定性。
3.3 GRACE参考观测值选取
由于GRACE数据和水文模型是两个独立的观测变量,但表达的是同一物理含义的量值,因此本研究利用二者互相约束来选取训练点。利用3.2节中介绍的不确定性分析方法,选取每个月不确定性最低的GRACE和GHMs产品作为卫星观测数据和模型模拟数据,并进行比较。然后设定经验阈值,当两类数据对应像素位置之间的差异小于该阈值时,则认为该点的GRACE观测值是误差较小的观测值,并将其选为参考值,而剩余位置的观测值为待校正值。
阈值的大小将直接影响训练点选取的准确性,如果阈值过小,会导致选取出的准确观测值数量过少,在建立校正模型时容易出现过拟合现象;而如果阈值过大,则会将准确性不高的观测值选入,影响校正模型的精度。
因此,研究将阈值以0.1 cm为步长,遍历0.1~20 cm之间所有的取值,并将每次选取出来的训练点与待校正点分别与GHMs的长时序信号变化进行定量分析。之所以将20 cm作为遍历的边界是因为两者之间差异大于20 cm时,研究区域中90%以上的点都可以作为训练点,此时再做校正的意义不大。
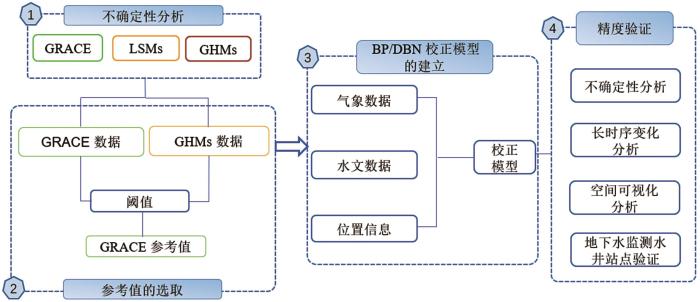
如图2所示,红色(蓝色)表示北美洲尺度上,不同阈值选出的待校正点(训练点)与GHMs月尺度水储量数据进行的长时序(2003年3月至2012年9月)定量分析。可以看到,无论是在相关性(R)还是在平均绝对误差(MAE)和均方根误差(RMSE)上,训练点计算出的水储量长时序变化均与GHMs模型更为接近。同时随着阈值的扩大,训练点的精度有所下降。因此,综合考虑相关性、平均绝对误差和均方根误差后,研究将经验阈值设置为2 cm。
图2
图2
根据不同阈值与GHMs进行长时序定量分析
Fig.2
Quantitative analysis of long time series with GHMs based on different thresholds (cm)
3.4 构建校正模型
根据3.3节得到的参考值,结合其对应位置上的气象、水文等辅助数据,通过神经网络建立校正模型进行训练,再使用该校正模型对其余位置上的观测值进行校正。
已有研究表明,来自LSMs模型的土壤含水量变化与GRACE观测得到的水储量变化具有高度的一致性[25],同时土壤含水量也是影响陆地水储量变化的重要因素之一,因此实验中首先将土壤含水量作为输入数据。其次,降水量与气温能够准确的反映一个区域的气候条件,同时也会通过地表径流、植物蒸腾作用等形式来影响整个区域的水储量变化,故将二者作为输入数据。最后,考虑到水储量在地理空间上的相关性,实验将能够反映位置信息的经纬度作为模型输入数据。
综上,实验在建立校正模型时,将经度、纬度、气温、降水量以及土壤含水量作为输入数据(均来自于LSMs中不确定性最低的模型),与训练点上的水储量异常值(Total Water Storage Anomaly,TWSA)进行建模。所谓水储量异常,指的是当前月的水储量,减去长时序的平均水储量。相较于水储量变化(后一月水储量减去前一月水储量),水储量异常值能更好地反映水储量是否亏损(盈余)以及亏损(盈余)程度。
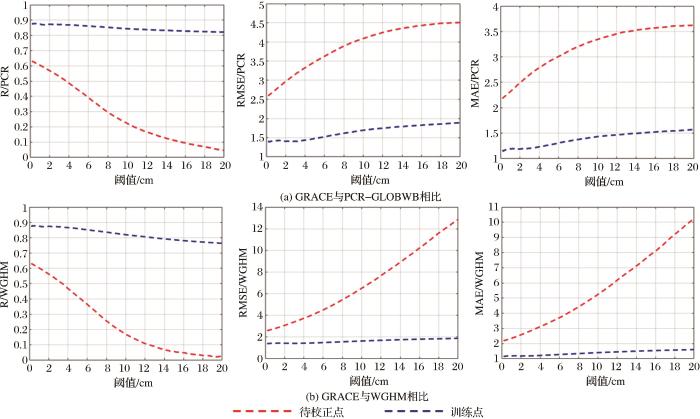
实验中对比了两个机器学习算法得到的校正结果。首先是BP网络,它的基本思想是,在网络的学习过程中使用梯度搜索技术,利用误差向后传播来修正权值,从而实现网络的实际输出与期望输出的均方差最小化[26]。实验中网络设置了一层神经元个数为5的隐藏层,隐含层激活函数为“tansig”函数。
图3
3.5 精度验证
研究从以下3个方面对GRACE校正结果进行精度验证与分析:首先,使用三角帽方法进行不同数据产品的不确定性定量分析;其次,对比GRACE产品(CSR、JPL和GFZ)、GHMs(WGHM和PCR-GLOBWB)与校正结果的水储量异常长时序变化与空间分布结果,并结合气温、降水和土壤湿度等气象辅助数据对结果进行定性分析;最后,从总水储量变化中提取地下水分量,基于USGS提供的地下水井实测数据,对结果进行站点验证。
4 结果与讨论
4.1 研究区概况
图4
4.2 产品间不确定性分析
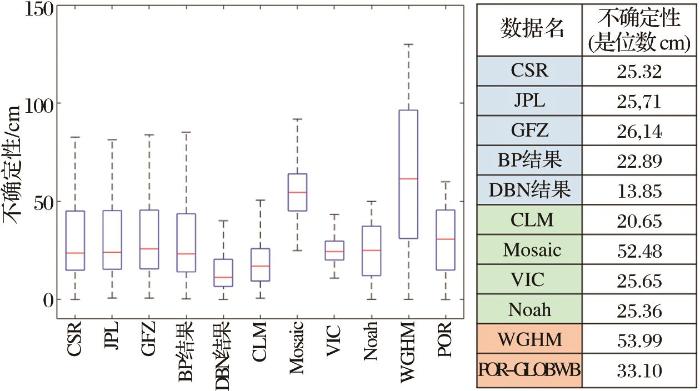
不确定性分析结果(图5)显示GHMs模型在水储量异常(TWSA)上具有更高的不确定性(WGHM: 53.99 cm,PCR-GLOBWB: 33.10 cm)。相对来说,GRACE观测数据与LSMs模拟结果的不确定性更为接近。而三类GRACE数据产品中CSR数据不确定性最低,为25.32 cm。结合GRACE观测数据与LSMs、GHMs模型模拟的数据特性进行融合,本研究校正结果表现出了更低的不确定性,其中DBN网络校正结果最佳(13.85 cm)。实验结果表明,利用本研究提出的方法融合多源水文数据能减少GRACE水储量数据中的不确定性。
图5
图5
不同产品间的不确定性分析结果
Fig.5
Uncertainties (cm) in TWS anomalies from different products
4.3 水储量异常长时序变化分析
由于在4.2节分析中,DBN网络校正结果表现出更低的不确定性,因此下文会将DBN网络结果作为代表,与全球水文模型及GRACE原始数据进行对比,进行长时序信号变化分析。
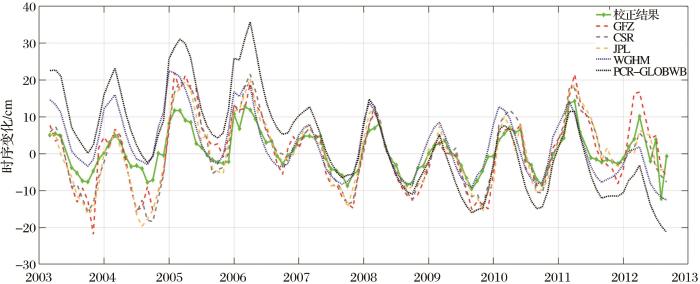
对于水储量长时序信号变化,目前比较通用的做法是与水文模型进行对比验证。通过图6可以直观的看到3个版本的GRACE水储量产品(CSR、GFZ、JPL)在长时序变化曲线上表现出了较大的差异,也进一步说明了不同处理流程为GRACE数据带来较大不确定性。校正结果的变化曲线相较于CSR、GFZ、JPL 3个版本的原始数据,变化更为平滑。而在不同版本GRACE数据一致性较好的时相上,校正结果也能较好地保持原始数据的变化趋势;因此,校正结果能够综合水文模型与GRACE观测,减少受到异常波动的影响。此外,水文模型结果整体的波动范围更大,与不确定性分析中水文模型具有更高不确定性的结果保持一致,这主要是因为模型中部分像素受到异常值的影响。
图6
图6
2003年3月~2012年9月校正结果水储量异常长时序变化分析
Fig.6
Quantitative analysis of DBN correction results from March 2003 to September 2012
4.3 空间分布可视化分析
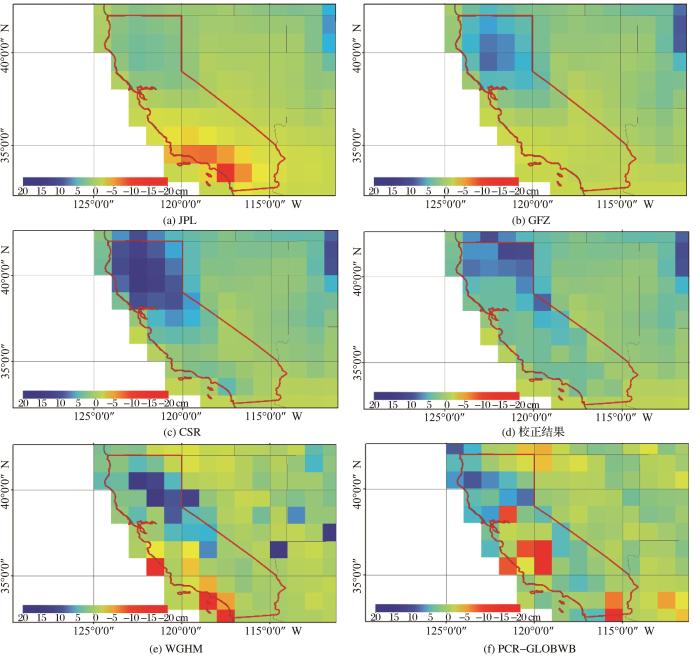
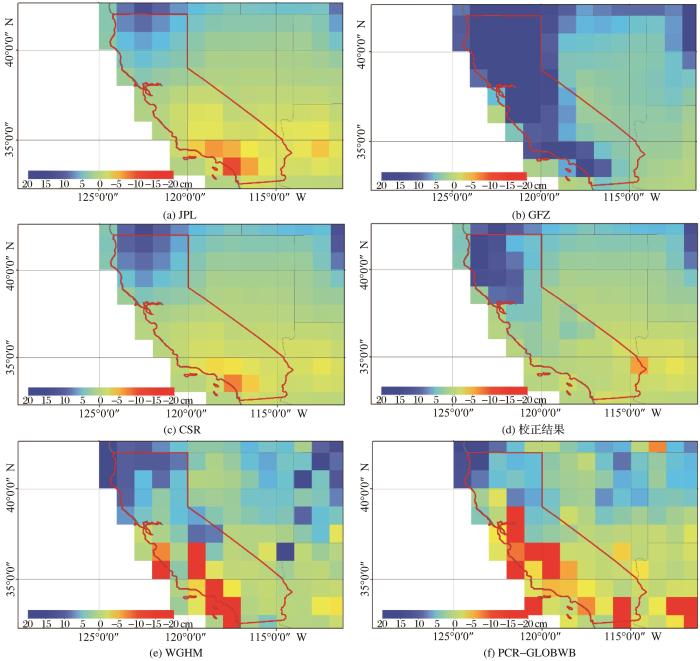
在本小节中,主要对比不同数据产品空间分布,并结合地下水、土壤含水量等辅助数据对模型校正结果进行分析验证。由于在2010年5月与2012年3月,GRACE水储量数据产品之间存在较大差异,因此,实验中选择这两个时相为例对校正方法的效果加以说明。
图7
图8
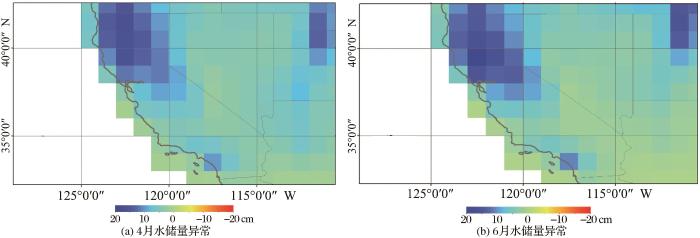
图8
2010年4和6月加州JPL水储量异常
Fig.8
California JPL total water storage anomaly in April and June 2010
图9
图9
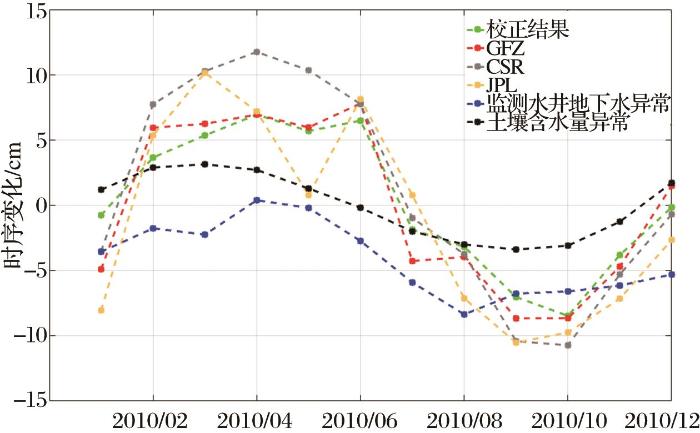
2010年加州水储量、地下水和土壤含水量异常时序变化
Fig.9
Time series of California TWSA, groundwater anomaly and soil moisture anomaly in 2010
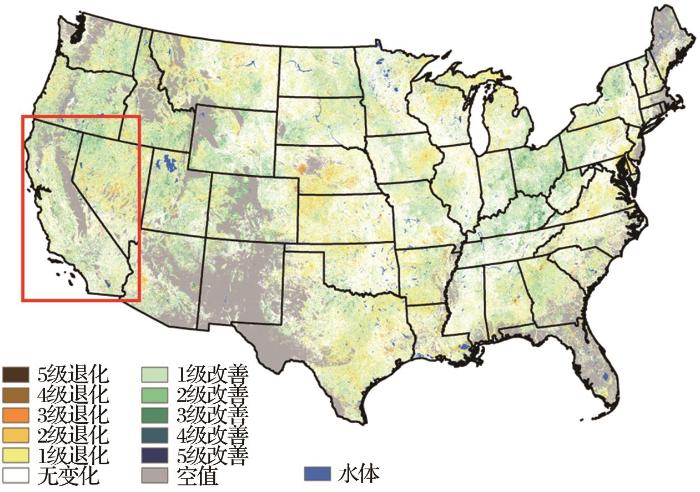
从图9中可以看出,加州属于夏季炎热干燥,冬季温和多雨的地中海气候,水储量往往会在夏季出现下降,而在冬季开始回升。就变化趋势而言,卫星观测数据、校正结果与地下水、土壤含水量异常基本保持一致,但JPL数据显示2010年4月至5月加州南部地区存在严重的水储量亏损(如图7(a)),使其时序信号在出现了急剧的下降,导致JPL水储量异常在2010年3月~6月表现出较大震荡,与地下水、土壤含水量的变化趋势,以及其他多源水文数据产品的结果均存在较大差异。此外,本研究参考了USGS发布的植被干旱指数图(图10,数据来源:
图10
图10
2010年4月至5月的植被干旱指数分布(数据来源:
Fig.10
Vegetation Drought Index (VegDRI) distribution map from April to May 2010
图11
图11
2012年3月加州水储量异常
Fig.11
California total water storage anomaly in March 2012
图12
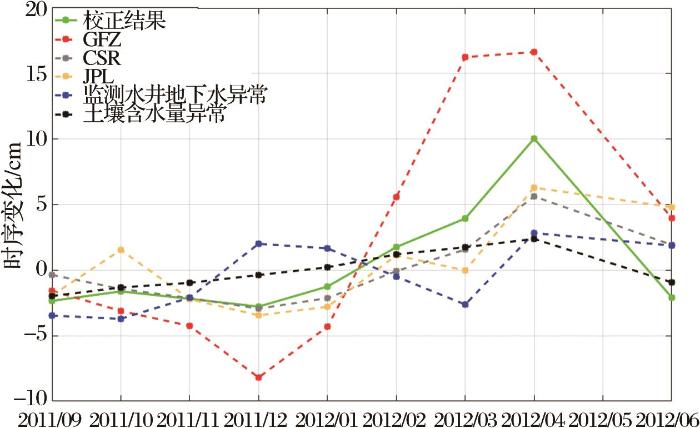
图12
2011年9月~2012年6月加州水储量、地下水和土壤含水量异常时序变化
Fig.12
Time series of California TWSA, groundwater anomaly and soil moisture anomaly from 2011 to June 2012
从图12中可以看到,2012年3月监测水井数据显示地下水出现轻微衰减,同时土壤含水量(缺少观测数据,故使用不确定性最低的LSMs模型数据)无明显增加,因此CSR、JPL与校正结果在该时相上水储量无明显变化。但GFZ数据则显示水储量有显著增加,与相关变量以及其他水储量产品的变化趋势产生了明显的差异。
分析上述结果可知,在不同时相上,GRACE产品间存在一定差异,这种差异随着时相不同并未表现出明显规律,还将影响水储量时序变化的趋势分析结果。本研究通过三角帽方法首先在每个时相上选取不确定性最低的产品,结合水文模型选取训练点,再利用水文参量的辅助数据建立回归校正模型,克服水储量数据中异常值对建模精度的影响。校正结果评价显示该方法能够有效降低月尺度GRACE水储量数据的不确定性
4.4 地下水井监测验证
由于GRACE观测到的总储水量变化由地表水,土壤含水和地下水三个部分组成。因此从GRACE计算出的水储量中减去地表水和土壤含水量即可获得地下水分量。
在不确定性分析中LSMs的CLM模型数据具有最低的不确定性,因此本研究将GRACE以及GHMs计算出的水储量异常减去CLM模型提供的地表水和土壤含水量异常,获取2003年3月至2012年9月之间的地下水异常数据,再使用USGS提供的监测水井水位数据进行站点验证(
图13
实验在单个时相上对研究区域内GRACE与对应监测水井得到的地下水异常取平均,然后进行长时序定量分析,结果如表3所示,可以看到结果与不确定性分析和长时序信号变化分析保持一致,校正后的结果相较于校正前相关性有所提升,其中DBN网络的结果具有最高的相关性0.55,同时在均方根误差与平均绝对误差上也优于原始数据和BP网络结果。
表3 监测水井站点验证结果
Table 3
| 数据名 | R | RMSE/cm | MAE/cm |
|---|---|---|---|
| CSR | 0.52 | 5.54 | 4.16 |
| JPL | 0.48 | 5.85 | 4.60 |
| GFZ | 0.52 | 6.03 | 4.43 |
| BP结果 | 0.52 | 5.62 | 4.36 |
| DBN结果 | 0.55 | 4.20 | 3.47 |
5 结 论
长时序、高精度的总储水量变化,对于深入理解全球水循环、监测地球气候与生态系统变化具有重要意义。本研究结合重力卫星观测数据与全球水文模型模拟数据,利用两者水储量数据间的互相约束来选取参考值,引入点面融合思想建立GRACE校正模型,实现GRACE卫星观测数据的精度校正。实验结果表明,校正结果在不确定分析中表现出更低的不确定性;同时在长时序变化和空间可视化分析中,校正结果相较于原始数据更为平滑,减少了异常的波动,并降低了GRACE数据间的不确定性。站点验证的结果表明校正后的相关性、均方根误差以及平均绝对误差中均有改善。同时实验中对比了BP神经网络和DBN的建模结果,其中DBN模型相比传统BP神经网络在本文实验中具有更好的效果。
参考文献
Contributions of GRACE to Understanding Climate Change
[J].
Global Sea Level Variations Estimated from Satellite Altimetry, GRACE and Oceanographic Data
[J].
联合卫星重力、卫星测高和海洋资料研究全球海平面变化
[J].
Terrestrial Water Storage Anomalies of Yangtze River Basin Droughts Observed by GRACE and Connections with ENSO
[J].
Global Models Underestimate Large Decadal Declining and Rising Water Storage Trends Relative to GRACE Satellite Data
[J].
Global Hydrology 2015: State, Trends, and Directions
[J].
Comparison and Assessment of Three Advanced Land Surface Models in Simulating Terrestrial Water Storage Components over the United States
[J].
Global Analysis of Spatiotemporal Variability in Merged Total Water Storage Changes Using Multiple GRACE Products and Global Hydrological Models
[J].
An Overview on High-Resolution Globalscale Hydrological Model
[J].
高分辨率全球尺度水文模型发展综述
[J].
Review of Assimilating GRACE Terrestrial Water Storage Data into Hydrological Models: Advances, Challenges and Opportunities
[J].
Review of the Post-processing Methods on GRACE Time Varied Gravity Data
[J].
GRACE时变重力数据的后处理方法研究进展
[J].
Review on the Recent Developments of Terrestrial Water Storage Variations Using GRACE Satellite-based Datum
[J].
应用GRACE卫星重力数据计算陆地水变化的相关进展评述
[J].
Low Degree Gravitational Changes from GRACE: Validation and Interpretation
[J].
Post-processing Removal of Correlated Errors in GRACE Data
[J].
Global Analysis of Approaches for Deriving Total Water Storage Changes from GRACE Satellites
[J].
Ensemble Prediction and Intercomparison Analysis of GRACE Time-variable Gravity Field Models
[J].
Global-scale Assessment of Groundwater Depletion and Related Groundwater Abstractions: Combining Hydrological Modeling with Information from Well Observations and GRACE Satellites
[J].
Drought and Flood Monitoring for a Large Karst Plateau in Southwest China Using Extended GRACE Data
[J].
Global Groundwater Storage Changes and Characteristics Observed by Satellite Gravimetry
[J].
卫星重力监测全球地下水储量变化及其特征
[J].
Using Satellite Observations to Assess Applicability of GLDAS and WGHM Hydrological Model
[J].
利用卫星观测数据评估GLDAS与WGHM水文模型的适用性
[J].
PCR-GLOBWB 2: A 5 Arcmin Global Hydrological and Water Resources Model
[J].
Improving Drought Simulations within the Murray-Darling Basin by Combined Calibration/Assimilation of GRACE Data into the Water GAP Global Hydrology Model
[J].
Uncertainty in Evapotranspiration from Land Surface Modeling, Remote Sensing, and GRACE Satellites
[J].
Uncertainties in GRACE-derived Terrestrial Water Storage Changes over Mainland China based on a Generalized Three–cornered Hat Method
[J].
利用广义三角帽方法评估GRACE反演中国大陆地区水储量变化的不确定性
[J].
A Revisited Three-cornered Hat Method for Estimating Frequency Standard Instability
[J].
GRACE Satellite Monitoring of Large Depletion in Water Storage in Response to the 2011 Drought in Texas
[J].
Learning Representations by Back-propagating Errors
[J].
A Fast Learning Algorithm for Deep Belief Nets
[J].
Training Restricted Boltzmann Machines: An introduction
[J].
Analysis of the California Climate Action Since the 1990s
[D].
S
[EB/OL]. ,
Ground Referencing GRACE Satellite Estimates of Groundwater Storage Changes in the California Central Valley, USA
[J].