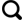地表粗糙度的测量计算方法及其对微波辐射散射的影响分析
孟春红 , 1 , 郭鹏 , 1 , 赵天杰 2 , 杨纲 1 , 李西灿 1 , 王博 1 , 万红 1 , 2
1.山东农业大学 信息科学与工程学院,山东 泰安 271018
2.中国科学院空天信息创新研究院,北京 100101
Measurement and Calculation Method of Surface Roughness and Its Impact on Microwave Radiation Scattering
Meng Chunhong , 1 , Guo Peng , 1 , Zhao Tianjie 2 , Yang Gang 1 , Li Xican 1 , Wang Bo 1 , Wan Hong 1 , 2
1.College of Information Science and Engineering,Shandong Agricultural University,Tai'an 271018,China
2.Aerospace Information Research Institute,Chinese Academy of Sciences,Beijing 100101,China
通讯作者: 郭鹏(1985-),男,山东泰安人,副教授,主要从事微波遥感地表参数定量反演及应用研究。E⁃mail: guopeng@sdau.edu.cn
收稿日期: 2020-01-17
修回日期: 2021-03-15
网络出版日期: 2021-07-21
基金资助:
国家重大科学研究计划项目“全球陆表能量与水分交换过程及其对全球变化作用的卫星观测与模拟研究” . 2015CB953700 民用航天“十三五”技术预先研究项目“陆地水资源卫星系统技术”,中国科学院青年创新促进会项目 . 2016061
Received: 2020-01-17
Revised: 2021-03-15
Online: 2021-07-21
摘要
地表粗糙度反映了地表的微小起伏,是土壤水分微波遥感反演研究中重要的地表参数。以闪电河流域为研究区,首先利用针板法对不同地物下的地表粗糙度进行测量,然后对测量数据进行透视变换、数字化、倾斜校正及周期校正等一系列的处理,计算得到不同地表的粗糙度结果。研究表明:在使用针板法测量地表粗糙度时,为校正不同剖面测量姿态的影响需要进行倾斜校正以减小计算偏差,而对胡萝卜地、花菜地等具有周期性田垄结构的地表还需要进一步进行周期校正。通过对获取的闪电河流域典型地物的地表粗糙度进行分析,发现该地区草地的地表粗糙度较小,作物区的地表粗糙度普遍偏大,各类地物的地表粗糙度由小到大分别为草地、花菜地、玉米地、胡萝卜地、土豆(收割)地和土豆(未收)地。最后对地表粗糙度与机载微波辐射、散射观测进行相关性分析,发现在地面单点测量的地表粗糙度与机载尺度的微波辐射散射特性之间不存在明显关系。
关键词:
遥感 地表粗糙度 均方根高度 自相关长度 校正
Abstract
The surface roughness reflects the small fluctuations of the surface and is an important surface parameter in the microwave remote sensing inversion of soil moisture. In this paper, the Lightning River Basin is used as the research area. First, the surface roughness of different ground objects is measured using the pin-plate method, and then a series of processing such as perspective transformation, digitization, tilt correction and period correction are performed on the measured data. Surface roughness results. Studies have shown that when measuring the surface roughness using the pin plate method, in order to correct the influence of the measurement attitude of different sections, tilt correction is required to reduce the calculation bias, and the ground surface with periodic ridge and ridge structure such as carrot field and cauliflower field needs further Perform period correction. By analyzing the surface roughness of typical objects in the Lightning River Basin, it is found that the surface roughness of the grassland in this area is small, the surface roughness of the crop area is generally large, and the surface roughness of various types of objects is from small to large They are grassland, cauliflower field, corn field, carrot field, potato (harvest) field, and potato (unreceived) field. Finally, the correlation analysis between the surface roughness and the airborne microwave radiation and scattering observations was conducted, and it was found that there was no obvious relationship between the surface roughness measured at the ground single point and the airborne scale microwave radiation scattering characteristics.
Keywords:
Remote sensing Surface roughness Root Mean Square Height(RMSH) Correlation Length(CL) Correction
本文引用格式
孟春红, 郭鹏, 赵天杰, 杨纲, 李西灿, 王博, 万红. 地表粗糙度的测量计算方法及其对微波辐射散射的影响分析 . 遥感技术与应用 [J], 2021, 36(3): 692-704 doi:10.11873/j.issn.1004-0323.2021.3.0692
Meng Chunhong, Guo Peng, Zhao Tianjie, Yang Gang, Li Xican, Wang Bo, Wan Hong. Measurement and Calculation Method of Surface Roughness and Its Impact on Microwave Radiation Scattering . Remote Sensing Technology and Application
1 引 言
地表粗糙度反映了地表的起伏状况,是许多陆面过程的主要影响因子[1 ] 。根据应用领域的差异,地表粗糙度可分为空气动力学粗糙度和几何粗糙度[2 ] 。空气动力学粗糙度通常用于气象学领域的研究,几何粗糙度多用在定量遥感领域。几何粗糙度通常以均方根高度S与自相关长度L两个相关参数表示,分别从垂直和水平的角度对地表粗糙度进行表征。
土壤水分是农业、水文、土壤学、环境学等领域的重要参数。目前,利用空间分辨率较高的微波遥感对土壤水分进行实时、动态、高精度和大范围的反演是研究和应用的热点[3 -4 ] 。在微波遥感领域,利用主动微波反演土壤水分所依赖的关键因子是后向散射系数,由于地表几何粗糙度对雷达后向散射系数具有显著的影响[5 -7 ] ,因此,几何粗糙度成为主动微波遥感领域研究的重点。同时,许多研究学者在被动微波反演土壤水分过程中发现了土壤水分与土壤粗糙度及其他关键因子之间的定量关系,从理论模型(IEM模型[8 ] 、AIEM模型[9 ] )到含有土壤粗糙度参数的半经验模型(Q/H模型[10 ] )。土壤水分反演算法中较为经典的半经验模型是Q/H模型,该模型包括极化混合因子Q,粗糙度参数H以及角度校正常数N等参数,但粗糙度效应的机理描述不够精确,改善对于粗糙度等关键影响参数的处理方法,是提高土壤水分产品质量的有效途径[10 -11 ] 。近年来,组合(几何)粗糙度在反演土壤水分中应用广泛,Zhao等[12 ] 认为大多数自然土壤表面更接近指数相关地表,其发现使用几何粗糙度参数S2 /L能够很好地刻画粗糙度效应,并由此发展了参数化的土壤微波辐射模型;Lawrence等[13 ] 发现利用半经验模型Q/H反演到的粗糙度参数H与ZS =S2 /L和极化混合因子Q直接相关;Zribi等[14 ] 发现组合粗糙度S2 /L在雷达反演土壤水分中也具有较好的效果;陈晶等[15 ] 提出适合相应地区土壤水分反演的组合粗糙度参数S3 /L2 。因此,获取准确的地表粗糙度对于微波遥感反演土壤水分发挥着关键性作用。
测量粗糙度有多种不同的方法。针对不同的测量方式,地表粗糙度测量分为接触式测量和非接触式测量。接触式测量主要包括针板法、链条法和差分GPS等;常用的非接触式测量包括近景摄影测量法、激光扫描法、红外线传感器法和超声波测距法等[16 ] 。目前,土壤表面粗糙度测量板方法(也称针板法)是遥感研究中普遍采用的土壤粗糙度测量方法,该装置构造较简易,尺寸适中,方便携带,适用于地表粗糙度的实地测量;通过拍摄获取土壤表面起伏的高度数据,采集成本低且便利,耗时短,测量效率高;由于测量针底端设有防护圆帽,测量针不会穿透地表插入土壤内部,避免了对土壤表面的破坏。针板法通过计算两个正交方向的均值以此反映整个研究样方的粗糙度。
地表粗糙度因其复杂性和各向异性,至今难以获取全球范围内的地表粗糙度,目前,大多数研究开展了特定区域内地表粗糙度的局部研究。依托中国科学院遥感科学院国家重点实验室组织开展的“碳循环、水循环和能量平衡遥感综合实验”飞行计划综合试验,以闪电河流域为研究区,利用针板法对选取的样方进行粗糙度测量,获取不同地物类型的地表高度数据,然后采用透视变换、测量数据数字化进行数据前期的预处理,采用倾斜校正剔除仪器本身和地表倾斜对地表粗糙度的影响,同时在作物区采用周期校正的方法校正周期性田垄结构对地表粗糙度造成的巨大偏差,最后得到了所测样方的均方根高度和自相关长度,并分析不同地物类型下的地表粗糙度的特点。最后对实际测量获取的地表粗糙度与机载微波辐射、散射观测进行相关性分析。由此形成的地表粗糙度测量与其对微波辐射散射的影响分析为该地区后续利用微波遥感反演地表土壤水分提供了实验分析依据。
2 研究区概况
闪电河流域是滦河上游的主要支流,发源于河北省丰宁县,流经河北省沽源县、正蓝旗、多伦县等地,地理坐标为114°55′~117°45′ E、41°46′~43°07′ N,地势西南高、东北低。属温带半干旱大陆性气候,降雨多集中在6~9月,多年年均降雨量为450~500 mm,多年平均蒸发量为1 188.3 mm。主要土地类型包括草地、耕地、林地和湿地等,主要种植土豆、莜麦和胡萝卜等农作物。
在闪电河流域水循环与能量平衡遥感综合试验[17 ] 中,与航空飞行试验同步进行了两个方向上的地表粗糙度测量,主要测量了闪电河流域南北航向以及东北西南航向中多个样方的地表粗糙度。其中,南北航线位于内蒙古自治区锡林郭勒盟正蓝旗县(115.990° E,42.241° N),河北省张家口市沽源县(115.688° E,41.669° N)所辖区域交界以及交界附近,东北—西南航线位于沽源县和承德市围场满族蒙古族自治县(117.761° E,41.938° N)所辖区域交界以及交界附近,如图1 所示。南北航向地域内地形复杂,典型地物种类繁多,具有草场、农用地、荒地、裸地和林地等具有代表性的地表覆盖种类,同一个大样方内不同地物类型所表现的地表起伏变化较大;东北西南航向地物类型简单,多为草地。试验期间共对61个不同地物类型的采样样方进行了粗糙度测量,南北航向的测量时间为2018年9月16日、17日,东南西北航向测量时间为2018年9月20日。其中草地采样样方19个,杂草地5个,胡萝卜地14个(其中未收割地10个,已收割4个),花菜地6个,玉米地4个(其中已收割3个,未收割1个),土豆地13个(已收割8个,未收割5个),如图1 所示。
图1
图1
研究区采样点分布图
Fig.1
Distribution map of the sample site in the study area
3 地表粗糙度测量与计算方法
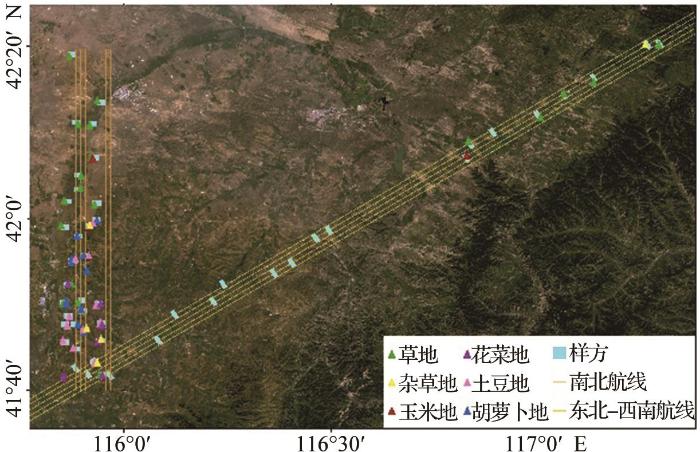
为获取较为准确的土壤粗糙度参数,必须进行严格的土壤粗糙度测量与计算,图2 为获取地表粗糙度的主要步骤。
图2
图2
地表粗糙度野外测量与粗糙度计算流程图
Fig.2
Flow chart of ground surface roughness measurement and calculation
3.1 地表粗糙度测量方法
3.1.1 土壤表面高度测量
地表粗糙度测量采用粗糙度测量板法(针板法)。针板全长100 cm,采样间隔1 cm,刻度安装自下而上每隔5 cm划分,用于量算测量针的起伏高度。图3 为粗糙度测量板示意图。具体的测量方法为:一方将针式粗糙度测量板插入待测地表,保证水准管上的两个方向的水管泡居中,另一方使用相机沿着与粗糙度测量板呈90°角的水平方向进行拍摄,拍摄时注意粗糙度测量板的4个角点不要存在任何遮挡,尽量不要有左右和上下的倾斜,同时记录好采样点地物类别,写在便利贴上,贴至粗糙度板的左右侧金属边框,拍照时一同拍摄进去,每个采样点分东西和南北方向观测,为了获取更稳定的测量结果,一般需要选取至少3 m长的剖面多个,对于此次测量所选用的粗糙度测量板,同一方向至少需要轮流观测3次,每次粗糙度板的安置尽量保持在同一条直线上,每次安放粗糙度板允许有少部分重叠区域。随后在室内对照片进行透视变换,同时将照片数字化显示以获得地表起伏。根据每个大样方中每个子样方的地表类型及复杂程度,选择比较典型的地表进行测量。若大样方中每个子样方植被类型相同,则只选择一个子样方进行测量;若大样方中每个子样方类型不一,每个小样方都需要测量。每个小样方平行于垄(或东西方向)测量3次,垂直于垄(或南北方向)测量3次,最后求取两个方向的均值作为该小样方的粗糙度参数。
图3
图3
针板法测量示意图
Fig.3
Needle plate method measurement chart
3.1.2 透视变换
拍取粗糙度照片过程中,因相机上下或者左右倾斜,导致粗糙度测量板无法正对相机光圈,易造成照片中粗糙度板呈现倾斜状态,倾斜的照片对后期数字化提取针头高度带来较大的高度误差,因而需要对照片做透视变换[18 -19 ] ,以此来校正拍照时角度倾斜的影响,透视变换实质是将图片投影到一个新的视平面[20 ] ,改变图像内部点的相对位置,使得已发生透视畸变的图像完成矫正的过程[21 ] 。透视变换可降低在土壤粗糙度参数计算过程中因图像倾斜引起的偏差。透视变换涉及矩阵计算,为避免计算量过大,先将原始图片裁剪,裁剪区域包含整个粗糙度板,裁剪之后,确定源图像中粗糙度板白色底板的4个角点坐标,定义目标图中白色底板4个顶点坐标,利用两幅图像4个同名点的坐标求取变换矩阵,进行透视变换使得整个图片投影到粗糙度板白色底板所在平面。以2号样方的子样方1(草地)为例,图4 (a)为拍摄的原始照片,透视变换结果如图4 (b)所示。从图中可以明显看出透视变换前粗糙度测量板白色底板所在的二维平面明显不与图片所在平面平行,变换后可以看出变换的图片是测量板白色底板的正视图。通过变换将测量中粗糙度测量板白色底板正视图的倾斜角度进行了纠正。
图4
图4
样方2号子样方1图像透视变换图
Fig.4
Perspective transformation of the image of the sample No. 2 sub-sample 1
3.1.3 土壤表面高度提取
将透视后的图片进行裁剪,只保留白色底板部分,利用PS软件新建一个与裁剪图同样大小的画布,依次描点(针头),并利用程序识别图中的黑点,统计每根针的像素个数,然后乘以比例尺(K=100 cm/图像列数),最终获取一系列较高精度的高度数据。2号样方的子样方1(草地)数字化后的高度如图5 所示。
图5
图5
测量数据数字化高度图
Fig.5
Digital height map of measured data
3.2 地表粗糙度计算方法
3.2.1 地表粗糙度参数计算
粗糙度参数是对地表凹凸状况的一种定量化表示。由于地表本身的各向异性,仅用一个参数无法将其特性进行合理化的表征,针对实际地表,往往利用多个参数进行粗糙度的刻画。同一地表根据角度不同定义了许多不同地表粗糙度相关参数,其中,基于地表廓线统计分析的传统粗糙度相关参数尤为经典。在微波遥感中通常用来表征地表粗糙度的参数有两类:一类是均方根高度S,用以刻画垂直方向上地表粗糙度;一类是自相关长度L,用来表征水平方向上的地表粗糙度状况 [22 -23 ] 。
(1)均方根高度S。均方根高度S是对地表高低起伏状况的定量化表示。假定X-Y平面内一点(x,y),其高度为Z,在表面上选择统计意义上具有代表性的一块,尺度分别为Lx 和Ly , 并将原点置于平面中心,则该表面平均高度为:
Z ¯ = 1 L x L y ∫ - L x / 2 L x / 2 ∫ - L y / 2 L y / 2 Z x , y d x d y (1)
Z 2 ¯ = 1 L x L y ∫ - L x / 2 L x / 2 ∫ - L y / 2 L y / 2 Z 2 x , y d x d y (2)
S = Z 2 ¯ - Z ¯ 2 1 / 2 (3)
对于实测一维离散数据,地表剖面的均方根高度S可表示为:
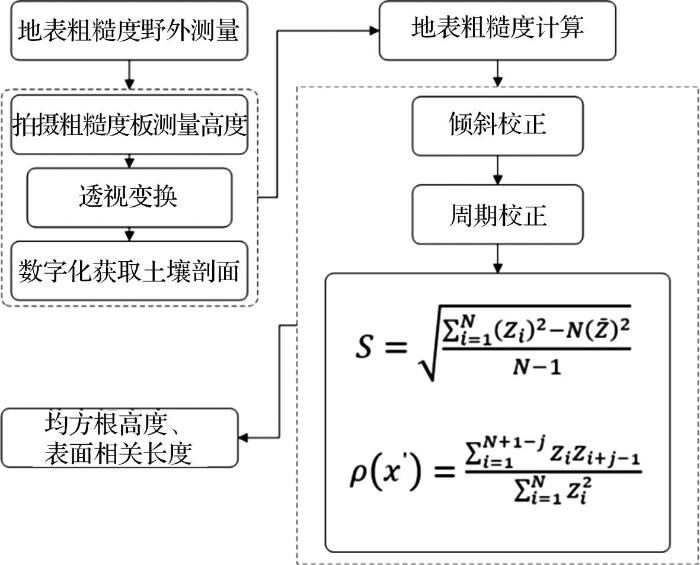
S = ∑ i = 1 N Z i 2 - N Z ˙ 2 N - 1 (4)
其中:N 为采样点个数,Zi 为采样点i 的表面高度,Z ˙ = 1 N ∑ i = 1 N Z i [5 ] 。
(2)表面相关长度L。表面相关长度被视为一个剖面上两点高度间相关性的一种度量。一维表面高度Z (x )的归一化自相关函数定义为:
ρ x ' = ∫ - L x / 2 L x / 2 Z ( x ) Z ( x + x ' ) d x ∫ - L x / 2 L x / 2 Z 2 ( x ) d x (5)
对于描述地表粗糙度的离散数据,归一化的自相关函数[1 ] 计算公式如下:
ρ x ' = ∑ i = 1 N + 1 - j Z i Z i + j - 1 ∑ i = 1 N Z i 2 (6)
其中:x’ 两采样点水平间距,j 为自然数。表面相关长度L 被定义为归一化自相关函数ρ x ' = 1 / e x’ 。一般来说,相关长度越小,地表越粗糙[1 ] 。在地表粗糙度的理论模型中,常用的表面自相关函数有高斯自相关函数:ρ ξ = e x p - ξ 2 l 2 ρ ξ = e x p ξ l ρ ξ = ( 1 + ξ 2 l 2 ) - 1.5
3.2.2 倾斜校正
针板法测量地表粗糙度在一定程度上会造成粗糙度测量板倾斜,加之地表自身的倾斜均会造成测量的高度数据倾斜,因此,采用粗糙度测量板获取的数据直接进行土壤粗糙度的计算与实际结果会存在很大的偏差,对后续地表粗糙度参数研究产生显著影响。为减小该类影响,在计算均方根高度和自相关长度前需要对数据进行倾斜校正。倾斜校正不同于透视变换,透视变换仅能纠正因透视投影形成的图像内部点与实际点的相对位置发生畸变的问题。
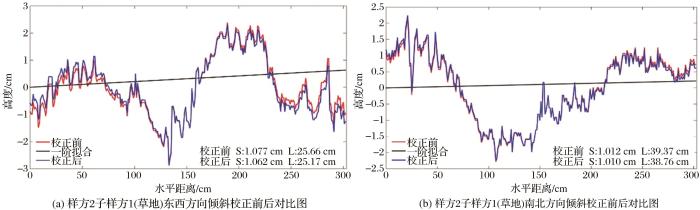
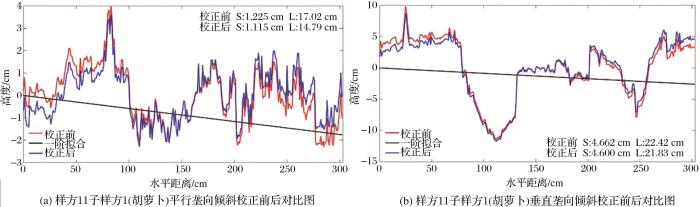
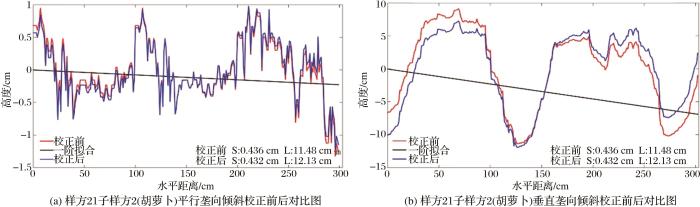
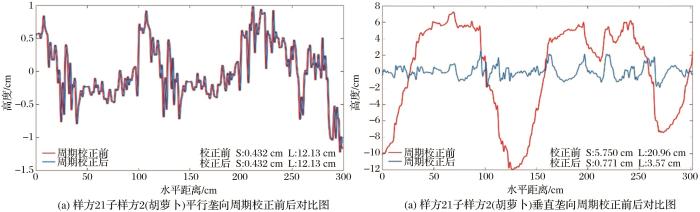
倾斜校正纠正的是在粗糙度板正视图下,因实际测量过程中测量板倾斜造成的数据倾斜,透视变换无法减小此类影响造成的偏差。倾斜校正的基本原理是对量测时针板倾斜所导致的垂直偏差进行校正,使其在同一水平线上显示垂直方向的高低起伏状况。倾斜校正采用数字化的实测数据获取一阶拟合的直线,利用数字化的测量数据与拟合直线上对应值做差获得地表高度波动数据,进一步求取地表高度波动数据与其均值的差值得到地表近似“水平”的剖面高度数据,以去除实测高度数据中的倾斜成分。以样方2子样方1(草地)、样方11子样方1(胡萝卜)以及样方21子样方2(胡萝卜)为例,在平行与垂直于垄两个方向上倾斜校正前后的数据对比如图6 ~图8 所示。
图6
图6
样方2子样方1(草地)倾斜校正前后对比图
Fig.6
Comparison of the tilt correction before and after the sample No.2 sub-sample 1
图7
图7
样方11子样方1(胡萝卜)倾斜校正前后对比图
Fig.7
Comparison of the tilt correction before and after the sample No.11 sub-sample 1
图8
图8
样方21子样方2(胡萝卜)倾斜校正前后对比图
Fig.8
Comparison of the tilt correction before and after the sample No.21 sub-sample 2
从图6 ~图8 可直观看出倾斜校正前后地表粗糙度参数存在一定差异,图中红色曲线代表倾斜校正前的地表高度波动,黑色直线是校正前地表高度数据的一阶拟合,代表其整体的斜率,蓝色曲线代表倾斜校正后的地表高度变化。S表示均方根高度,L代表自相关长度。图6 (a)显示样方2号子样方1(草地)平行于垄方向倾斜校正前的均方根高度为1.077 cm,自相关长度为25.66 cm,校正后其均方根高度为1.062 cm,自相关长度为25.17 cm;图6 (b)中样方2号子样方1垂直于垄方向倾斜校正前的均方根高度为1.012 cm,自相关长度为39.37 cm,校正后其均方根高度为1.01 cm,自相关长度为38.76 cm。图7 (a)中样方11号子样方1(胡萝卜地)平行于垄方向倾斜校正前的均方根高度为1.225 cm,自相关长度为17.02 cm,校正后其均方根高度为1.115 cm,自相关长度为14.79 cm;图7 (b)中样方11号子样方1垂直于垄方向倾斜校正前的均方根高度为4.662 cm,自相关长度为22.42 cm,校正后其均方根高度为4.6 cm,自相关长度为21.83 cm。图8 (a)呈现样方21号子样方2(胡萝卜地)平行于垄方向倾斜校正前的均方根高度为0.436 cm,自相关长度为11.48 cm,校正后其均方根高度为0.432 cm,自相关长度为12.13 cm;图8 (b)中样方21号子样方2垂直于垄方向倾斜校正前的均方根高度为6.092 cm,自相关长度为22.84 cm,校正后其均方根高度为5.57 cm,自相关长度为20.96 cm。图6 表明草地两个相互垂直方向的均方根高度更为接近,说明草地的整体高度波动较小,图7 与图8 呈现出胡萝卜地等作物区与草地平行垄向的粗糙度参数较为一致,而垂直垄向的均方根高度普遍偏大,其原因可能是垂直垄向上存在周期性田垄结构,属于含有人为因素影响的复杂地表,计算某一样方的粗糙度参数所取的是两个垂直方向的参数均值,垂直垄向均方根高度过大会对粗糙度最终计算结果造成不利影响,因此还需要进行进一步的周期性校正。
3.2.3 周期校正
作物区地表粗糙度不仅与数据倾斜密切相关,同时也受周期性田垄结构的影响,周期性田垄结构具有各向异性,在垂直垄向方向上,表面粗糙度受大尺度垄结构特性影响,而在平行垄方向上,表面粗糙度主要受表面的小尺度起伏影响。如果不进行周期性校正,表面粗糙度参数的各向异性会非常严重。研究表明周期性表面计算的地表粗糙度会导致模拟的雷达后向散射系数或者被动微波亮温产生误差[24 ] 。去除周期性田垄结构的影响,有利于提高作物区地表粗糙度的精度[25 ] 。周期校正采用的方法是首先对数字化的测量数据进行最小二乘拟合获取最佳拟合曲线,并记录下最佳拟合曲线上与测量数据相对应的拟合值,利用数字化的测量数据与拟合数据的差值获取作物区去除田垄结构影响的用于计算地表粗糙度参数的地表高度数据。对于包含人为因素的复杂地表(如农田),仅进行倾斜校正并不能满足其精度要求,须对数据作进一步处理分析。
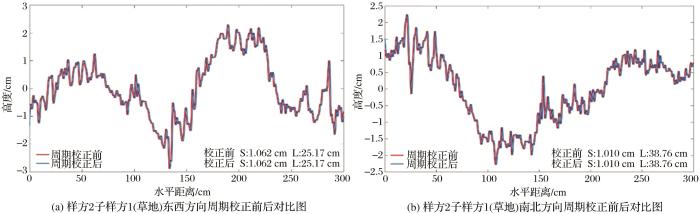
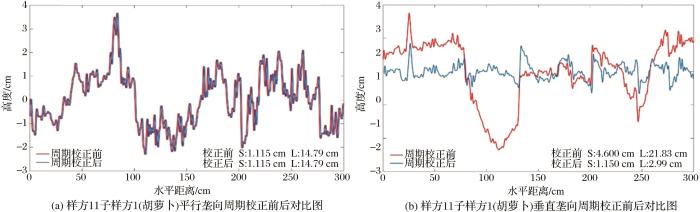
2号样方子样方1、11号样方子样方1和21号样方子样方2的两个相互垂直方向的周期校正前后对比分别如图9 ~图11 所示。图9 的结果显示样方2号子样方1相互垂直的两个方向地表粗糙度参数不受周期校正的影响,其校正前后东西方向的均方根高度均为1.062 cm,自相关长度均为25.17 cm;南北方向校正前后的均方根高度均无变化。图10 和图11 表明针对同一作物区,进行周期校正前,平行垄向和垂直垄向地表粗糙度呈现较明显偏差。未进行周期校正时,样方11号子样方1(胡萝卜地)平行垄向周期校正前后粗糙度参数无变化;样方21号子样方2平行于垄向周期校正前后的均方根高度均为0.432 cm,自相关长度均为12.13 cm。对于平行于垄向的地表粗糙度不受周期性田垄结构的影响,该项数据处理过程中可不进行周期校正。针对垂直于垄方向,样方11号子样方1周期校正前的均方根高度为4.6 cm,自相关长度为21.83 cm,周期校正后的均方根高度为1.15 cm,自相关长度为2.99 cm;周期校正前21号样方子样方2的均方根高度为5.75 cm,自相关长度为20.96 cm;周期校正后该样方的均方根高度为0.771 cm,自相关长度为3.57 cm,周期校正前后垂直于垄向的数据结果呈现显著差异。如果不进行周期校正,最终计算的粗糙度参数会明显高估。
图9
图9
样方2子样方1(草地)周期校正前后对比图
Fig.9
Comparison chart before and after cycle correction of the sample No. 2 sub-sample 1
图10
图10
样方11子样方1(胡萝卜)周期校正前后对比图
Fig.10
Comparison chart before and after cycle correction of the sample No. 11 sub-sample 1
图11
图11
样方21子样方2(胡萝卜)周期校正前后对比图
Fig.11
Comparison chart before and after cycle correction of the sample No. 21 sub-sample 2
4 结果与分析
4.1 闪电河流域地表粗糙度空间分布特征
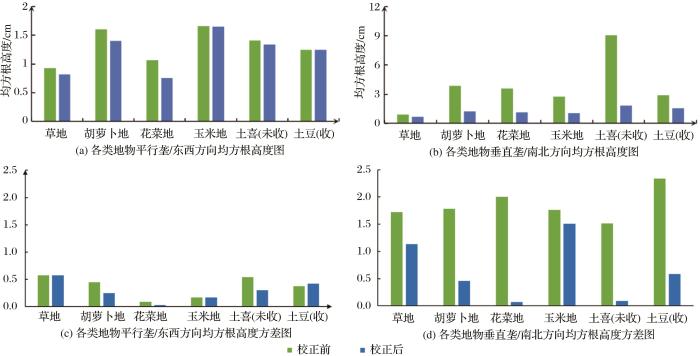
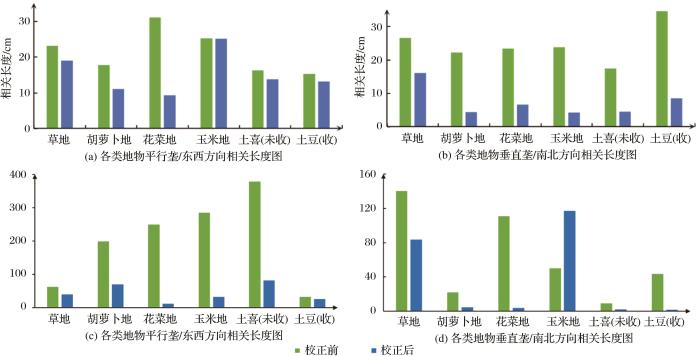
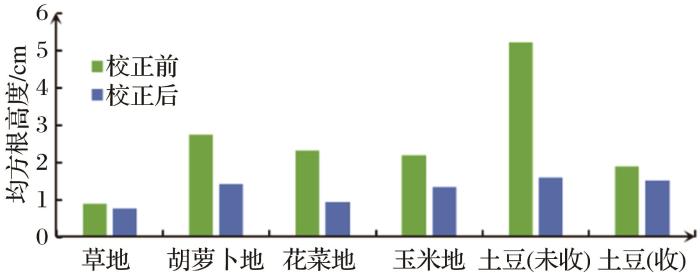
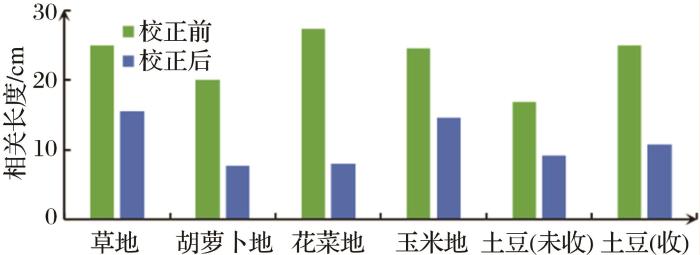
根据以上处理过程完成各类地物下地表高度数据的倾斜校正、周期校正等数据处理,各类地物在不同方向上校正前后平均值和方差统计结果分别如图12 、图13 和表1 所示,各类地物下地表粗糙度参数平均值计算结果如图14 、图15 和表2 所示。
图12
图12
各类地物不同方向的地表均方根高度均值与方差统计图
Fig.12
Statistical map of mean and variance of the surface Root Mean Square Height (RMSH) of various land cover types in different directions
图13
图13
各类地物不同方向的地表相关长度均值与方差统计图
Fig.13
Statistical map of mean and variance of the surface Correlation Length (CL) of various land cover types in different directions
图14
图14
各类地物下地表平均均方根高度均值统计图
Fig.14
Statistical graph of average Root Mean Square Height (RMSH) for various land cover types
图15
图15
各类地物下地表平均相关长度方差统计图
Fig.15
Statistical graph of average surface Correlation Length (CL) for various land cover types
分析结果发现不同地表的粗糙度参数呈现显著差异,且不同地物在不同方向的地表粗糙度测量结果具有明显的差异性。校正后各类地物下的地表粗糙度参数值均有降低,但不同作物类型的校正结果具有较大的差异性,由图12 、图13 以及表1 分析可知,草地的东西和南北两个方向校正前后参数变化较小,其东西方向校正前均方根高度为0.925 cm,自相关长度为23.191 cm,校正后降为0.818 cm,自相关长度降为19.06 cm;南北方向校正前的均方根高度为0.899 cm,自相关长度为26.578 cm,校正后分别降为0.704 cm和16.065 cm。平行于垄向的花菜地均方根高度在各类作物中变化最大,胡萝卜地次之,土豆地变动较小,玉米地的均方根高度在各类作物中波动最小。作物区垂直于垄向与平行垄向相比校正前后降幅偏大,形成这一结果的原因是周期性田垄结构引起的校正过程中倾斜角度增大;对垂直于垄方向只进行倾斜校正,草地的地表高度数据是更接近于地表水平的剖面高度,而作物区的地表均方根高度呈现明显的高估,均方根高度均在2 cm以上,最高已达9.067 cm,对作物区的地表高度数据进行周期校正后的均方根高度均在0~2.5 cm的范围内波动,与平行于垄向的结果相近,各类样方的平均地表粗糙度参数由平行于垄以及垂直于垄两个方向的均值来表示,统计结果如图14 、图15 和表2 所示。各类地物下的均方根高度由小到大依次为草地、花菜地、玉米地、胡萝卜地、土豆(收割)地、土豆(未收)地。各地类的地表相关长度差异显著, 表2 中给出了作物区校正后的平均相关长度。其中草地的地表相关长度最大为15.57 cm,玉米地次之,胡萝卜地、花菜地、土豆(收割)地和土豆(未收)地普遍偏小,与各地物下的均方根高度大体呈现负相关。并且校正后大部分地物的均方根高度方差都明显减小,尤其是垂直垄方向的土豆地和花菜地。
研究区内草地平均均方根高度为0.754 cm,相关长度为15.57 cm,地势整体起伏较小,地表粗糙度较小;作物区受人为因素影响,各类作物下的平均均方根高度大多集中在1~2 cm,不同地类平均地表相关长度差异显著,相关长度介于5~15 cm之间。作物区地表起伏程度较草地偏大,草地相对较平坦。研究结果表明研究区内粗糙度的空间分布与地表覆盖密切相关。从方差的统计结果来看,校正后大部分地物的地表参数的方差都明显减小,尤其是对于有明显田垄结构的作物区,在垂直垄向的均方根高度的方差校正后减小明显,如胡萝卜地、花菜地和土豆地,这也进一步证明了校正的必要性。
在计算相关长度过程中,常用表面自相关函数来描述随机地表在水平距离上两个点的高度之间的自相关程度。在理论模型中,土壤表面的自相关函数通常有高斯相关、指数相关和1.5倍功率自相关3种。在计算获取实际测量样方地表的相关函数时,将已经计算得到的相关长度值代入高斯、指数相关函数,首先获得理论上的自相关曲线,然后将计算得到的样方地表的自相关函数曲线与理论的自相关函数曲线进行对比,计算的自相关函数曲线与哪种理论的曲线更接近,就取该种自相关函数作为该土壤表面的自相关函数类型。根据自相关函数的计算结果分析,具有田垄结构的农作物样方(土豆地、花菜地、胡萝卜地和玉米地)平行于垄方向地势起伏较小,自相关函数多为指数相关,垂直于垄方向由于田垄的存在,使得地表变得粗糙,其自相关函数多为高斯相关。其中,6个花菜地采样样方中的4个,13个土豆地采样样方中的9个,14个胡萝卜地采样样方中的7个,4个玉米地采样样方中的2个都具有在平行垄方向为指数相关函数,垂直垄方向为高斯相关函数的规律。在其他不满足这种规律的采样样方中,自相关函数多为指数相关。对于没有明显田垄结构的草地和杂草地,地势平坦,地表相对光滑,自相关函数多为指数相关,其中19个草地的采样样方中有15个为指数相关,5个杂草地采样样方中有4个为指数相关。因此,根据计算结果分析可以得出,平滑地表接近指数自相关函数,粗糙地表更接近高斯自相关函数。对于普通的自然地表,指数相关能更好的模拟其随机变化,这与前人的研究具有很好的一致性[26 ] 。
4.2 地表粗糙度对微波辐射散射的影响
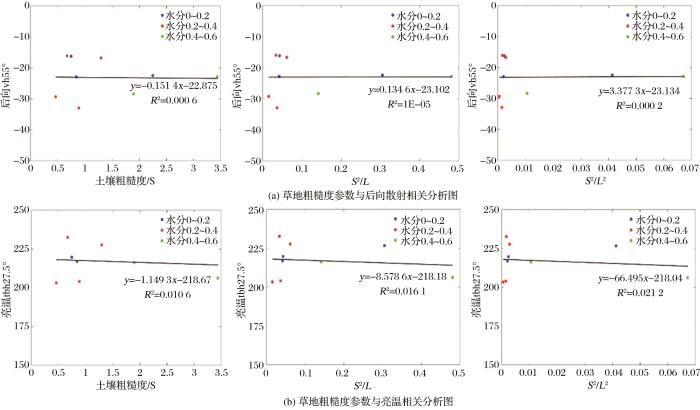
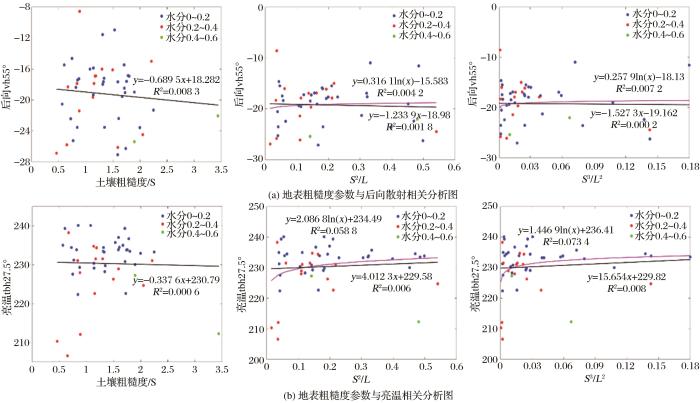
将获取的地表粗糙度参数(选取均方根高度)及组合粗糙度参数(S 2 /L 、S 3 /L 2 )分别与机载飞行观测的主动微波后向散射系数和被动微波亮温数据进行相关性分析,因主动微波的各入射角各极化条件下相关分析结果相似,被动微波的各极化条件下相关分析结果近似,故此处以主动微波55°入射角的VH极化后向散射和被动微波27.5°的H极化亮温为例,并结合不同区间的土壤水分,相关分析结果如图16 、图17 所示。
图16
图16
草地粗糙度与微波散射辐射相关分析图
Fig.16
Correlation analysis chart of grassland roughness and microwave scattering radiation
图17
图17
地表粗糙度与微波散射辐射相关分析图
Fig.17
Correlative analysis chart of surface roughness and microwave scattered radiation
图16 和图17 中黑线代表土壤粗糙度参数分别和后向散射、亮温数据的一阶拟合结果,玫红线代表其对数拟合结果。由于草地的粗糙度相对变化较小,因此图16 以草地为例,由一阶拟合结果及其相关系数R 2 表明草地的均方根高度分别与机载后向散射及被动微波亮温并不存在直接的线性相关,草地的组合粗糙度参数(S 2 /L 、S 3 /L 2 )与机载微波辐射散射均无明显的相关性;不同土壤水分下的地表粗糙度和后向散射与亮温存在显著差异。图17 中一阶拟合结果及其相关系数R 2 显示研究区内的整体地表粗糙度(不考虑土壤水分)与机载后向散射及被动微波亮温的变化未呈明确的相关性;对组合粗糙度参数(S 2 /L 、S 3 /L 2 ) 与机载后向散射及被动微波亮温进行对数拟合的相关系数较一阶拟合更高,但是整体而言与机载后向散射及被动微波亮温的变化未呈明确的相关性;由散点图可知土壤水分介于0.2~0.4 m³/m³之间的地表粗糙度增加,其后向散射与亮温均有增加的趋势,且组合粗糙度参数(S 2 /L 、S 3 /L 2 )下的后向散射与亮温变化趋势较均方根高度S效果更显著,间接表明后向散射及亮温和地表粗糙度、土壤水分之间存在一定关系。
随着粗糙度的变化,地表的微波辐射散射并无明显的变化趋势,主要原因是机载微波辐射散射并非仅受地表粗糙度的影响,而受多种环境因素包括植被含水量及其结构、土壤水分等共同作用,在本文的研究中很难将以上因素进行严格剔除。另外,机载观测的尺度在百米(雷达)到公里(辐射计)量级,而地面粗糙度的测量只在单点进行,而地表粗糙度的空间变异性非常强,二者之间存在不可调和的尺度差异。后续还需对影响其变化的多个因素做深入研究分析。
5 结 论
在微波遥感中,获取地表粗糙度实测数据的主要方法是采用粗糙度测量板法(针板法)。通过针板法获取闪电河流域典型地物下的地表高度数据,并通过透视变换、倾斜校正、周期校正等方法完成数据处理。结果表明进行倾斜校正、周期校正等数据处理可以有效地校正地表粗糙度测量过程中外界因素的影响;最后得到了研究区内所测样方的均方根高度和自相关长度,获取了闪电河流域典型地物的地表粗糙度。实验通过对典型地物地表粗糙度的计算及其对微波辐射散射的影响分析,得到以下结论:
(1)利用针板法进行的粗糙度测量时,因受仪器以及地表倾斜的影响,对所有测量数据均须进行倾斜校正处理,即各类地物下的高度数据均须进行倾斜校正。
(2)作物区因受人为耕作影响存在周期性田垄结构,在垂直于垄方向计算粗糙度参数时会造成较大误差,须先进行倾斜校正,并进一步进行周期校正,如玉米地、花菜地等;对于草地等不具有田垄结构的地物和作物区平行于田垄方向的地表高度数据由于不受田垄结构的影响,无需进行周期校正。
(3)闪电河流域内草地地势较平坦,地表粗糙度参数普遍偏小,作物区受人为种植的影响,地表粗糙度参数普遍偏大,各类地物的地表粗糙度由小到大依次为草地、花菜地、玉米地、胡萝卜地、土豆(收割)地、土豆(未收)地。
(4) 地表粗糙度及组合粗糙度参数(S 2 /L 、S 3 /L 2 )与机载微波辐射散射均无简单的线性的相关性。随着粗糙度增加,地表的机载微波辐射散射并无明确的变化趋势。为了研究地表粗糙度对微波辐射和散射的影响,需要后期于对影响其变化的多个因素做深入研究。
研究所形成的地表粗糙度测量计算方法其对微波辐射散射的影响分析对于利用微波遥感反演土壤水分算法的发展具有一定的意义;另一方面也为该地区后续利用微波遥感定量反演中的地表参数化奠定了基础。
参考文献
View Option
[1]
Jiang Chongya Fang Hongliang Wei Shanshan A Summary of Research on Parameterization of Surface Roughness
[J]. Progress in Earth Science , 2012 ,27 (3 ): 292 -303 .
[本文引用: 3]
江冲亚 , 方红亮 , 魏珊珊 地表粗糙度参数化研究综述
[J]. 地球科学进展 , 2012 , 27 (3 ):292 -303 .
[本文引用: 3]
[2]
Zhu Caiying Zhang Renhua Wang Jinfeng et al Quantitative Retrieval of Two-dimensional Distribution of Surface Aerodynamic Roughness Using SAR Images and TM Thermal Infrared Images
[J]. Science in China: Earth Sciences , 2004 , 34 (4 ):385 -393 .
[本文引用: 1]
朱彩英 , 张仁华 , 王劲峰 , 等 运用SAR图像和TM热红外图像定量反演地表空气动力学粗糙度的二维分布
[J]. 中国科学:地球科学 , 2004 , 34 (4 ):385 -393 .
[本文引用: 1]
[3]
Chen Luwan Han Ling Qin Xiaobao et al A New Method for Constructing Roughness Parameters in Soil Moisture from Microwave Remote Sensing
[J]. Geography and Geographic Information Science , 2017 ,33 (6 ):37 -43 ,2 .
[本文引用: 1]
陈鲁皖 , 韩玲 , 秦小宝 , 等 微波遥感反演土壤水分中构建粗糙度参数的新方法
[J]. 地理与地理信息科学 ,2017 ,33 (6 ):37 -43 ,2 .
[本文引用: 1]
[4]
Chen Si Research on Inversion of Soil Surface Roughness based on Optical and SAR Data
[D]. Beijing : University of Chinese Academy of Sciences , 2019 .
[本文引用: 1]
陈思 基于光学和SAR数据的土壤表面粗糙度反演研究
[D].北京 :中国科学院大学(中国科学院东北地理与农业生态研究所) ,2019 .
[本文引用: 1]
[5]
Davidson M W J Toan T L Mattia F et al On the Characterization of Agricultural Soil Roughness for Radar Remote Sensing Studies
[J]. IEEE Transactions on Geoscience and Remote Sensing ,2000 ,38 (2 ):630 -640 . doi:10.1109/36.841993 .
[本文引用: 2]
[6]
Zhao Tianjie Zhang Lixin Jiang Lingmei et al Joint Inversion of Soil Moisture Using Active and Passive Microwave Data
[J]. Advances in Earth Science , 2009 ,24 (7 ): 769 -775 .
赵天杰 , 张立新 , 蒋玲梅 , 等 利用主被动微波数据联合反演土壤水分
[J]. 地球科学进展 , 2009 ,24 (7 ): 769 -775 .
[7]
Ulaby F T Batlivala P P Dobson M C Microwave Backscatter Dependence on Surface Roughness, Soil Moisture, and Soil Texture: Part I-Bare Soil
[J]. IEEE Transactions on Geoscience Electronics , 1978 , 16 (4 ): 286 -295 .doi:10.1109/TGE.1978.294586 .
[本文引用: 1]
[8]
Fung A K Li Z Chen K S Backscattering from a Randomly Rough Dielectric Surface
[J]. IEEE Transactions on Geoscience and Remote Sensing ,1992 ,30 (2 ):356 -369 .doi:10.1109/36.134085 .
[本文引用: 1]
[9]
Chen K S Wu T D Tsang L et al Emission of Rough Surfaces Calculated by the Integral Equation Method with Comparison to Three-dimensional Moment Method Simulation
[J]. IEEE Transactions on Geoscience and Remote Sensing , 2003 , 41 (1 ):90 -101 . doi:10.1109/TGRS.2002.807587 .
[本文引用: 1]
[10]
Zhao Tianjie New Developments and Future Prospects of Passive Microwave Inversion of Soil Moisture in L-band
[J]. Progress in Geography , 2018 ,37 (2 ): 198 -213 .
[本文引用: 2]
赵天杰 被动微波反演土壤水分的L波段新发展及未来展望
[J]. 地理科学进展 , 2018 , 37 (2 ): 198 -213 .
[本文引用: 2]
[11]
Zhao Tianjie Passive Microwave Remote Sensing of Soil Moisture
[D]. Beijing :Beijing Normal University , 2012 .
[本文引用: 1]
赵天杰 被动微波遥感土壤水分
[D].北京 :北京师范大学 ,2012 .
[本文引用: 1]
[12]
Zhao T J Shi J C Bindlish R et al Parametric Exponentially Correlated Surface Emission Model for L-band Passive Microwave Soil Moisture Retrieval
[J]. Physics and Chemistry of the Earth , Parts A/B/C, 2015 ,83 :65 -74 .doi:10.1016/j.pce.2015.04.001 .
[本文引用: 1]
[13]
Lawrence H Wigneron J P Demontoux F et al Evaluating the Semiempirical H-Q Model Used to Calculate the L-band Emissivity of a Rough Bare Soil
[J]. IEEE Transactions on Geoscience and Remote Sensing , 2013 , 51 (7 ): 4075 -4084 .doi:10.1109/TGRS.2012.22269 95 .
[本文引用: 1]
[14]
Zribi M Dechambre M A New Empirical Model to Retrieve soil Moisture and Roughness from C-band Radar Data
[J]. Remote Sensing of Environment ,2002 ,84 (1 ):42 -52 . doi:10.1016/S0034-4257(02)00069-X .
[本文引用: 1]
[15]
Chen Jing Jia Yi Yu Fan Retrieval of Bare Surface Soil Moisture with Dual Polarization Radar
[J]. Transactions of the Chinese Society of Agricultural Engineering , 2013 , 29 (10 ):109 -116 .
[本文引用: 1]
陈晶 , 贾毅 , 余凡 双极化雷达反演裸露地表土壤水分
[J]. 农业工程学报 , 2013 ,29 (10 ): 109 -116 .
[本文引用: 1]
[16]
Tao Haoran Chen Quan Li Zhen et al Close-range Photogrammetry Improves the Accuracy of Bare Surface Roughness Measurement
[J]. Transactions of the Chinese Society of Agricultural Engineering , 2017 ,33 (15 ):162 -167 .
[本文引用: 1]
陶浩然 ,陈权 ,李震 ,等 近景摄影测量提高裸露地表粗糙度测量精度
[J]. 农业工程学报 ,2017 ,33 (15 ): 162 -167 .
[本文引用: 1]
[17]
Zhao Tianjie Shi Jiancheng Liqing Lü et al Comprehensive Remote Sensing Experiment of Water Cycle and Energy Balance in the Shandian River Basin
[J]. National Remote Sensing Bulletin , 2020 ,25 (4 ):1 -17 .
[本文引用: 1]
赵天杰 , 施建成 , 吕利清 , 等 闪电河流域水循环和能量平衡遥感综合试验
[J]. 遥感学报 , 2020 , 25 (4 ):1 -17 .
[本文引用: 1]
[18]
Thomas J Kareem A Bowyer K Fast Robust Perspective Transform Estimation for Automatic Image Registration in Disaster Response Applications
[C]∥ Geoscience and Remote Sensing Symposium , 2012 .
[本文引用: 1]
[19]
Su Z Zhu S Lü X et al Image Restoration Using Structured Sparse Representation with a Novel Parametric Data-Adaptive Transformation Matrix
[J]. Image Communication , 2017 , 52 (3 ):151 -172 .doi:10.10 16/j.image.2017.01.003 .
[本文引用: 1]
[20]
Xu Yanping Research on Visualization Method of A-pillar Blind Zone based on 3D Reconstruction and Perspective Transformation
[D].Changchun :Jilin University , 2019 .许彦平. 基于三维重构与透视变换的汽车A柱盲区可视化方法研究[D].长春:吉林大学 ,2019.
[本文引用: 1]
[21]
Wu Di Huang Wenqian Wang Ying Derivation of Perspective Projection Transformation Matrix in Graphic Transformation
[J]. Hydrographic Surveying and Charting , 2003 ,23 (1 ):18 -21 .
[本文引用: 1]
吴迪 ,黄文骞 ,王莹 图形变换中透视投影变换矩阵的推导
[J].海洋测绘 , 2003 ,23 (1 ): 18 -21 .
[本文引用: 1]
[22]
Evans D L Farr T G Zyl J J V Estimates of Surface Roughness Derived from Synthetic Aperture Radar(SAR) Data
[J]. IEEE Transactions on Geoscience and Remote Sensing , 1992 , 30 (2 ):382 -389 .doi:10.1109/36.134087 .
[本文引用: 1]
[23]
Lü J R Xie Y S Luo H Erosion Process and Temporal Variations in the Soil Surface Roughness of Spoil Heaps under Multi-Day Rainfall Simulation
[J]. Remote Sensing ,2020 ,12 (14 ):2192 . doi:10.3390/rs12142192 .
[本文引用: 1]
[24]
Jin A K Lin S L Chuang S L Microwave Thermal Emission from Periodic Surfaces
[J]. IEEE Transactions on Geoscience and Remote Sensing , 2007 , GE-22 (4 ): 377 - 382 .doi:10.1109/TGRS.1984.350640 .
[本文引用: 1]
[25]
Zheng Xingming Zhao Kai Li Xiaojie Measurement and Accuracy Analysis of Surface Roughness Parameters in Farmland
[J]. Journal of Geo-Information Science , 2013 ,15 (5 ): 752 -760 .
[本文引用: 1]
郑兴明 , 赵凯 , 李晓洁 农田表面粗糙度参数的测量与精度分析
[J]. 地球信息科学学报 ,2013 ,15 (5 ):752 -760 .
[本文引用: 1]
[26]
Schwank M Volksch I Wigneron J P et al Comparison of Two Bare-soil Reflectivity Models and Validation with L-band Radiometer Measurements
[J]. IEEE Transactions on Geoscience and Remote Sensing , 2010 ,48 (1 ):325 - 337 .doi:10.1109/TGRS.2009.2026894 .
[本文引用: 1]
地表粗糙度参数化研究综述
3
2012
... 地表粗糙度反映了地表的起伏状况,是许多陆面过程的主要影响因子[1 ] .根据应用领域的差异,地表粗糙度可分为空气动力学粗糙度和几何粗糙度[2 ] .空气动力学粗糙度通常用于气象学领域的研究,几何粗糙度多用在定量遥感领域.几何粗糙度通常以均方根高度S与自相关长度L两个相关参数表示,分别从垂直和水平的角度对地表粗糙度进行表征. ...
... 对于描述地表粗糙度的离散数据,归一化的自相关函数[1 ] 计算公式如下: ...
... 其中:x’ 两采样点水平间距,j 为自然数.表面相关长度L 被定义为归一化自相关函数ρ x ' = 1 / e x’ .一般来说,相关长度越小,地表越粗糙[1 ] .在地表粗糙度的理论模型中,常用的表面自相关函数有高斯自相关函数:ρ ξ = e x p - ξ 2 l 2 ρ ξ = e x p ξ l ρ ξ = ( 1 + ξ 2 l 2 ) - 1.5 . ...
地表粗糙度参数化研究综述
3
2012
... 地表粗糙度反映了地表的起伏状况,是许多陆面过程的主要影响因子[1 ] .根据应用领域的差异,地表粗糙度可分为空气动力学粗糙度和几何粗糙度[2 ] .空气动力学粗糙度通常用于气象学领域的研究,几何粗糙度多用在定量遥感领域.几何粗糙度通常以均方根高度S与自相关长度L两个相关参数表示,分别从垂直和水平的角度对地表粗糙度进行表征. ...
... 对于描述地表粗糙度的离散数据,归一化的自相关函数[1 ] 计算公式如下: ...
... 其中:x’ 两采样点水平间距,j 为自然数.表面相关长度L 被定义为归一化自相关函数ρ x ' = 1 / e x’ .一般来说,相关长度越小,地表越粗糙[1 ] .在地表粗糙度的理论模型中,常用的表面自相关函数有高斯自相关函数:ρ ξ = e x p - ξ 2 l 2 ρ ξ = e x p ξ l ρ ξ = ( 1 + ξ 2 l 2 ) - 1.5 . ...
运用SAR图像和TM热红外图像定量反演地表空气动力学粗糙度的二维分布
1
2004
... 地表粗糙度反映了地表的起伏状况,是许多陆面过程的主要影响因子[1 ] .根据应用领域的差异,地表粗糙度可分为空气动力学粗糙度和几何粗糙度[2 ] .空气动力学粗糙度通常用于气象学领域的研究,几何粗糙度多用在定量遥感领域.几何粗糙度通常以均方根高度S与自相关长度L两个相关参数表示,分别从垂直和水平的角度对地表粗糙度进行表征. ...
运用SAR图像和TM热红外图像定量反演地表空气动力学粗糙度的二维分布
1
2004
... 地表粗糙度反映了地表的起伏状况,是许多陆面过程的主要影响因子[1 ] .根据应用领域的差异,地表粗糙度可分为空气动力学粗糙度和几何粗糙度[2 ] .空气动力学粗糙度通常用于气象学领域的研究,几何粗糙度多用在定量遥感领域.几何粗糙度通常以均方根高度S与自相关长度L两个相关参数表示,分别从垂直和水平的角度对地表粗糙度进行表征. ...
微波遥感反演土壤水分中构建粗糙度参数的新方法
1
2017
... 土壤水分是农业、水文、土壤学、环境学等领域的重要参数.目前,利用空间分辨率较高的微波遥感对土壤水分进行实时、动态、高精度和大范围的反演是研究和应用的热点[3 -4 ] .在微波遥感领域,利用主动微波反演土壤水分所依赖的关键因子是后向散射系数,由于地表几何粗糙度对雷达后向散射系数具有显著的影响[5 -7 ] ,因此,几何粗糙度成为主动微波遥感领域研究的重点.同时,许多研究学者在被动微波反演土壤水分过程中发现了土壤水分与土壤粗糙度及其他关键因子之间的定量关系,从理论模型(IEM模型[8 ] 、AIEM模型[9 ] )到含有土壤粗糙度参数的半经验模型(Q/H模型[10 ] ).土壤水分反演算法中较为经典的半经验模型是Q/H模型,该模型包括极化混合因子Q,粗糙度参数H以及角度校正常数N等参数,但粗糙度效应的机理描述不够精确,改善对于粗糙度等关键影响参数的处理方法,是提高土壤水分产品质量的有效途径[10 -11 ] .近年来,组合(几何)粗糙度在反演土壤水分中应用广泛,Zhao等[12 ] 认为大多数自然土壤表面更接近指数相关地表,其发现使用几何粗糙度参数S2 /L能够很好地刻画粗糙度效应,并由此发展了参数化的土壤微波辐射模型;Lawrence等[13 ] 发现利用半经验模型Q/H反演到的粗糙度参数H与ZS =S2 /L和极化混合因子Q直接相关;Zribi等[14 ] 发现组合粗糙度S2 /L在雷达反演土壤水分中也具有较好的效果;陈晶等[15 ] 提出适合相应地区土壤水分反演的组合粗糙度参数S3 /L2 .因此,获取准确的地表粗糙度对于微波遥感反演土壤水分发挥着关键性作用. ...
微波遥感反演土壤水分中构建粗糙度参数的新方法
1
2017
... 土壤水分是农业、水文、土壤学、环境学等领域的重要参数.目前,利用空间分辨率较高的微波遥感对土壤水分进行实时、动态、高精度和大范围的反演是研究和应用的热点[3 -4 ] .在微波遥感领域,利用主动微波反演土壤水分所依赖的关键因子是后向散射系数,由于地表几何粗糙度对雷达后向散射系数具有显著的影响[5 -7 ] ,因此,几何粗糙度成为主动微波遥感领域研究的重点.同时,许多研究学者在被动微波反演土壤水分过程中发现了土壤水分与土壤粗糙度及其他关键因子之间的定量关系,从理论模型(IEM模型[8 ] 、AIEM模型[9 ] )到含有土壤粗糙度参数的半经验模型(Q/H模型[10 ] ).土壤水分反演算法中较为经典的半经验模型是Q/H模型,该模型包括极化混合因子Q,粗糙度参数H以及角度校正常数N等参数,但粗糙度效应的机理描述不够精确,改善对于粗糙度等关键影响参数的处理方法,是提高土壤水分产品质量的有效途径[10 -11 ] .近年来,组合(几何)粗糙度在反演土壤水分中应用广泛,Zhao等[12 ] 认为大多数自然土壤表面更接近指数相关地表,其发现使用几何粗糙度参数S2 /L能够很好地刻画粗糙度效应,并由此发展了参数化的土壤微波辐射模型;Lawrence等[13 ] 发现利用半经验模型Q/H反演到的粗糙度参数H与ZS =S2 /L和极化混合因子Q直接相关;Zribi等[14 ] 发现组合粗糙度S2 /L在雷达反演土壤水分中也具有较好的效果;陈晶等[15 ] 提出适合相应地区土壤水分反演的组合粗糙度参数S3 /L2 .因此,获取准确的地表粗糙度对于微波遥感反演土壤水分发挥着关键性作用. ...
基于光学和SAR数据的土壤表面粗糙度反演研究
1
2019
... 土壤水分是农业、水文、土壤学、环境学等领域的重要参数.目前,利用空间分辨率较高的微波遥感对土壤水分进行实时、动态、高精度和大范围的反演是研究和应用的热点[3 -4 ] .在微波遥感领域,利用主动微波反演土壤水分所依赖的关键因子是后向散射系数,由于地表几何粗糙度对雷达后向散射系数具有显著的影响[5 -7 ] ,因此,几何粗糙度成为主动微波遥感领域研究的重点.同时,许多研究学者在被动微波反演土壤水分过程中发现了土壤水分与土壤粗糙度及其他关键因子之间的定量关系,从理论模型(IEM模型[8 ] 、AIEM模型[9 ] )到含有土壤粗糙度参数的半经验模型(Q/H模型[10 ] ).土壤水分反演算法中较为经典的半经验模型是Q/H模型,该模型包括极化混合因子Q,粗糙度参数H以及角度校正常数N等参数,但粗糙度效应的机理描述不够精确,改善对于粗糙度等关键影响参数的处理方法,是提高土壤水分产品质量的有效途径[10 -11 ] .近年来,组合(几何)粗糙度在反演土壤水分中应用广泛,Zhao等[12 ] 认为大多数自然土壤表面更接近指数相关地表,其发现使用几何粗糙度参数S2 /L能够很好地刻画粗糙度效应,并由此发展了参数化的土壤微波辐射模型;Lawrence等[13 ] 发现利用半经验模型Q/H反演到的粗糙度参数H与ZS =S2 /L和极化混合因子Q直接相关;Zribi等[14 ] 发现组合粗糙度S2 /L在雷达反演土壤水分中也具有较好的效果;陈晶等[15 ] 提出适合相应地区土壤水分反演的组合粗糙度参数S3 /L2 .因此,获取准确的地表粗糙度对于微波遥感反演土壤水分发挥着关键性作用. ...
基于光学和SAR数据的土壤表面粗糙度反演研究
1
2019
... 土壤水分是农业、水文、土壤学、环境学等领域的重要参数.目前,利用空间分辨率较高的微波遥感对土壤水分进行实时、动态、高精度和大范围的反演是研究和应用的热点[3 -4 ] .在微波遥感领域,利用主动微波反演土壤水分所依赖的关键因子是后向散射系数,由于地表几何粗糙度对雷达后向散射系数具有显著的影响[5 -7 ] ,因此,几何粗糙度成为主动微波遥感领域研究的重点.同时,许多研究学者在被动微波反演土壤水分过程中发现了土壤水分与土壤粗糙度及其他关键因子之间的定量关系,从理论模型(IEM模型[8 ] 、AIEM模型[9 ] )到含有土壤粗糙度参数的半经验模型(Q/H模型[10 ] ).土壤水分反演算法中较为经典的半经验模型是Q/H模型,该模型包括极化混合因子Q,粗糙度参数H以及角度校正常数N等参数,但粗糙度效应的机理描述不够精确,改善对于粗糙度等关键影响参数的处理方法,是提高土壤水分产品质量的有效途径[10 -11 ] .近年来,组合(几何)粗糙度在反演土壤水分中应用广泛,Zhao等[12 ] 认为大多数自然土壤表面更接近指数相关地表,其发现使用几何粗糙度参数S2 /L能够很好地刻画粗糙度效应,并由此发展了参数化的土壤微波辐射模型;Lawrence等[13 ] 发现利用半经验模型Q/H反演到的粗糙度参数H与ZS =S2 /L和极化混合因子Q直接相关;Zribi等[14 ] 发现组合粗糙度S2 /L在雷达反演土壤水分中也具有较好的效果;陈晶等[15 ] 提出适合相应地区土壤水分反演的组合粗糙度参数S3 /L2 .因此,获取准确的地表粗糙度对于微波遥感反演土壤水分发挥着关键性作用. ...
On the Characterization of Agricultural Soil Roughness for Radar Remote Sensing Studies
2
2000
... 土壤水分是农业、水文、土壤学、环境学等领域的重要参数.目前,利用空间分辨率较高的微波遥感对土壤水分进行实时、动态、高精度和大范围的反演是研究和应用的热点[3 -4 ] .在微波遥感领域,利用主动微波反演土壤水分所依赖的关键因子是后向散射系数,由于地表几何粗糙度对雷达后向散射系数具有显著的影响[5 -7 ] ,因此,几何粗糙度成为主动微波遥感领域研究的重点.同时,许多研究学者在被动微波反演土壤水分过程中发现了土壤水分与土壤粗糙度及其他关键因子之间的定量关系,从理论模型(IEM模型[8 ] 、AIEM模型[9 ] )到含有土壤粗糙度参数的半经验模型(Q/H模型[10 ] ).土壤水分反演算法中较为经典的半经验模型是Q/H模型,该模型包括极化混合因子Q,粗糙度参数H以及角度校正常数N等参数,但粗糙度效应的机理描述不够精确,改善对于粗糙度等关键影响参数的处理方法,是提高土壤水分产品质量的有效途径[10 -11 ] .近年来,组合(几何)粗糙度在反演土壤水分中应用广泛,Zhao等[12 ] 认为大多数自然土壤表面更接近指数相关地表,其发现使用几何粗糙度参数S2 /L能够很好地刻画粗糙度效应,并由此发展了参数化的土壤微波辐射模型;Lawrence等[13 ] 发现利用半经验模型Q/H反演到的粗糙度参数H与ZS =S2 /L和极化混合因子Q直接相关;Zribi等[14 ] 发现组合粗糙度S2 /L在雷达反演土壤水分中也具有较好的效果;陈晶等[15 ] 提出适合相应地区土壤水分反演的组合粗糙度参数S3 /L2 .因此,获取准确的地表粗糙度对于微波遥感反演土壤水分发挥着关键性作用. ...
... 其中:N 为采样点个数,Zi 为采样点i 的表面高度,Z ˙ = 1 N ∑ i = 1 N Z i [5 ] . ...
Microwave Backscatter Dependence on Surface Roughness, Soil Moisture, and Soil Texture: Part I-Bare Soil
1
1978
... 土壤水分是农业、水文、土壤学、环境学等领域的重要参数.目前,利用空间分辨率较高的微波遥感对土壤水分进行实时、动态、高精度和大范围的反演是研究和应用的热点[3 -4 ] .在微波遥感领域,利用主动微波反演土壤水分所依赖的关键因子是后向散射系数,由于地表几何粗糙度对雷达后向散射系数具有显著的影响[5 -7 ] ,因此,几何粗糙度成为主动微波遥感领域研究的重点.同时,许多研究学者在被动微波反演土壤水分过程中发现了土壤水分与土壤粗糙度及其他关键因子之间的定量关系,从理论模型(IEM模型[8 ] 、AIEM模型[9 ] )到含有土壤粗糙度参数的半经验模型(Q/H模型[10 ] ).土壤水分反演算法中较为经典的半经验模型是Q/H模型,该模型包括极化混合因子Q,粗糙度参数H以及角度校正常数N等参数,但粗糙度效应的机理描述不够精确,改善对于粗糙度等关键影响参数的处理方法,是提高土壤水分产品质量的有效途径[10 -11 ] .近年来,组合(几何)粗糙度在反演土壤水分中应用广泛,Zhao等[12 ] 认为大多数自然土壤表面更接近指数相关地表,其发现使用几何粗糙度参数S2 /L能够很好地刻画粗糙度效应,并由此发展了参数化的土壤微波辐射模型;Lawrence等[13 ] 发现利用半经验模型Q/H反演到的粗糙度参数H与ZS =S2 /L和极化混合因子Q直接相关;Zribi等[14 ] 发现组合粗糙度S2 /L在雷达反演土壤水分中也具有较好的效果;陈晶等[15 ] 提出适合相应地区土壤水分反演的组合粗糙度参数S3 /L2 .因此,获取准确的地表粗糙度对于微波遥感反演土壤水分发挥着关键性作用. ...
Backscattering from a Randomly Rough Dielectric Surface
1
1992
... 土壤水分是农业、水文、土壤学、环境学等领域的重要参数.目前,利用空间分辨率较高的微波遥感对土壤水分进行实时、动态、高精度和大范围的反演是研究和应用的热点[3 -4 ] .在微波遥感领域,利用主动微波反演土壤水分所依赖的关键因子是后向散射系数,由于地表几何粗糙度对雷达后向散射系数具有显著的影响[5 -7 ] ,因此,几何粗糙度成为主动微波遥感领域研究的重点.同时,许多研究学者在被动微波反演土壤水分过程中发现了土壤水分与土壤粗糙度及其他关键因子之间的定量关系,从理论模型(IEM模型[8 ] 、AIEM模型[9 ] )到含有土壤粗糙度参数的半经验模型(Q/H模型[10 ] ).土壤水分反演算法中较为经典的半经验模型是Q/H模型,该模型包括极化混合因子Q,粗糙度参数H以及角度校正常数N等参数,但粗糙度效应的机理描述不够精确,改善对于粗糙度等关键影响参数的处理方法,是提高土壤水分产品质量的有效途径[10 -11 ] .近年来,组合(几何)粗糙度在反演土壤水分中应用广泛,Zhao等[12 ] 认为大多数自然土壤表面更接近指数相关地表,其发现使用几何粗糙度参数S2 /L能够很好地刻画粗糙度效应,并由此发展了参数化的土壤微波辐射模型;Lawrence等[13 ] 发现利用半经验模型Q/H反演到的粗糙度参数H与ZS =S2 /L和极化混合因子Q直接相关;Zribi等[14 ] 发现组合粗糙度S2 /L在雷达反演土壤水分中也具有较好的效果;陈晶等[15 ] 提出适合相应地区土壤水分反演的组合粗糙度参数S3 /L2 .因此,获取准确的地表粗糙度对于微波遥感反演土壤水分发挥着关键性作用. ...
Emission of Rough Surfaces Calculated by the Integral Equation Method with Comparison to Three-dimensional Moment Method Simulation
1
2003
... 土壤水分是农业、水文、土壤学、环境学等领域的重要参数.目前,利用空间分辨率较高的微波遥感对土壤水分进行实时、动态、高精度和大范围的反演是研究和应用的热点[3 -4 ] .在微波遥感领域,利用主动微波反演土壤水分所依赖的关键因子是后向散射系数,由于地表几何粗糙度对雷达后向散射系数具有显著的影响[5 -7 ] ,因此,几何粗糙度成为主动微波遥感领域研究的重点.同时,许多研究学者在被动微波反演土壤水分过程中发现了土壤水分与土壤粗糙度及其他关键因子之间的定量关系,从理论模型(IEM模型[8 ] 、AIEM模型[9 ] )到含有土壤粗糙度参数的半经验模型(Q/H模型[10 ] ).土壤水分反演算法中较为经典的半经验模型是Q/H模型,该模型包括极化混合因子Q,粗糙度参数H以及角度校正常数N等参数,但粗糙度效应的机理描述不够精确,改善对于粗糙度等关键影响参数的处理方法,是提高土壤水分产品质量的有效途径[10 -11 ] .近年来,组合(几何)粗糙度在反演土壤水分中应用广泛,Zhao等[12 ] 认为大多数自然土壤表面更接近指数相关地表,其发现使用几何粗糙度参数S2 /L能够很好地刻画粗糙度效应,并由此发展了参数化的土壤微波辐射模型;Lawrence等[13 ] 发现利用半经验模型Q/H反演到的粗糙度参数H与ZS =S2 /L和极化混合因子Q直接相关;Zribi等[14 ] 发现组合粗糙度S2 /L在雷达反演土壤水分中也具有较好的效果;陈晶等[15 ] 提出适合相应地区土壤水分反演的组合粗糙度参数S3 /L2 .因此,获取准确的地表粗糙度对于微波遥感反演土壤水分发挥着关键性作用. ...
被动微波反演土壤水分的L波段新发展及未来展望
2
2018
... 土壤水分是农业、水文、土壤学、环境学等领域的重要参数.目前,利用空间分辨率较高的微波遥感对土壤水分进行实时、动态、高精度和大范围的反演是研究和应用的热点[3 -4 ] .在微波遥感领域,利用主动微波反演土壤水分所依赖的关键因子是后向散射系数,由于地表几何粗糙度对雷达后向散射系数具有显著的影响[5 -7 ] ,因此,几何粗糙度成为主动微波遥感领域研究的重点.同时,许多研究学者在被动微波反演土壤水分过程中发现了土壤水分与土壤粗糙度及其他关键因子之间的定量关系,从理论模型(IEM模型[8 ] 、AIEM模型[9 ] )到含有土壤粗糙度参数的半经验模型(Q/H模型[10 ] ).土壤水分反演算法中较为经典的半经验模型是Q/H模型,该模型包括极化混合因子Q,粗糙度参数H以及角度校正常数N等参数,但粗糙度效应的机理描述不够精确,改善对于粗糙度等关键影响参数的处理方法,是提高土壤水分产品质量的有效途径[10 -11 ] .近年来,组合(几何)粗糙度在反演土壤水分中应用广泛,Zhao等[12 ] 认为大多数自然土壤表面更接近指数相关地表,其发现使用几何粗糙度参数S2 /L能够很好地刻画粗糙度效应,并由此发展了参数化的土壤微波辐射模型;Lawrence等[13 ] 发现利用半经验模型Q/H反演到的粗糙度参数H与ZS =S2 /L和极化混合因子Q直接相关;Zribi等[14 ] 发现组合粗糙度S2 /L在雷达反演土壤水分中也具有较好的效果;陈晶等[15 ] 提出适合相应地区土壤水分反演的组合粗糙度参数S3 /L2 .因此,获取准确的地表粗糙度对于微波遥感反演土壤水分发挥着关键性作用. ...
... [10 -11 ].近年来,组合(几何)粗糙度在反演土壤水分中应用广泛,Zhao等[12 ] 认为大多数自然土壤表面更接近指数相关地表,其发现使用几何粗糙度参数S2 /L能够很好地刻画粗糙度效应,并由此发展了参数化的土壤微波辐射模型;Lawrence等[13 ] 发现利用半经验模型Q/H反演到的粗糙度参数H与ZS =S2 /L和极化混合因子Q直接相关;Zribi等[14 ] 发现组合粗糙度S2 /L在雷达反演土壤水分中也具有较好的效果;陈晶等[15 ] 提出适合相应地区土壤水分反演的组合粗糙度参数S3 /L2 .因此,获取准确的地表粗糙度对于微波遥感反演土壤水分发挥着关键性作用. ...
被动微波反演土壤水分的L波段新发展及未来展望
2
2018
... 土壤水分是农业、水文、土壤学、环境学等领域的重要参数.目前,利用空间分辨率较高的微波遥感对土壤水分进行实时、动态、高精度和大范围的反演是研究和应用的热点[3 -4 ] .在微波遥感领域,利用主动微波反演土壤水分所依赖的关键因子是后向散射系数,由于地表几何粗糙度对雷达后向散射系数具有显著的影响[5 -7 ] ,因此,几何粗糙度成为主动微波遥感领域研究的重点.同时,许多研究学者在被动微波反演土壤水分过程中发现了土壤水分与土壤粗糙度及其他关键因子之间的定量关系,从理论模型(IEM模型[8 ] 、AIEM模型[9 ] )到含有土壤粗糙度参数的半经验模型(Q/H模型[10 ] ).土壤水分反演算法中较为经典的半经验模型是Q/H模型,该模型包括极化混合因子Q,粗糙度参数H以及角度校正常数N等参数,但粗糙度效应的机理描述不够精确,改善对于粗糙度等关键影响参数的处理方法,是提高土壤水分产品质量的有效途径[10 -11 ] .近年来,组合(几何)粗糙度在反演土壤水分中应用广泛,Zhao等[12 ] 认为大多数自然土壤表面更接近指数相关地表,其发现使用几何粗糙度参数S2 /L能够很好地刻画粗糙度效应,并由此发展了参数化的土壤微波辐射模型;Lawrence等[13 ] 发现利用半经验模型Q/H反演到的粗糙度参数H与ZS =S2 /L和极化混合因子Q直接相关;Zribi等[14 ] 发现组合粗糙度S2 /L在雷达反演土壤水分中也具有较好的效果;陈晶等[15 ] 提出适合相应地区土壤水分反演的组合粗糙度参数S3 /L2 .因此,获取准确的地表粗糙度对于微波遥感反演土壤水分发挥着关键性作用. ...
... [10 -11 ].近年来,组合(几何)粗糙度在反演土壤水分中应用广泛,Zhao等[12 ] 认为大多数自然土壤表面更接近指数相关地表,其发现使用几何粗糙度参数S2 /L能够很好地刻画粗糙度效应,并由此发展了参数化的土壤微波辐射模型;Lawrence等[13 ] 发现利用半经验模型Q/H反演到的粗糙度参数H与ZS =S2 /L和极化混合因子Q直接相关;Zribi等[14 ] 发现组合粗糙度S2 /L在雷达反演土壤水分中也具有较好的效果;陈晶等[15 ] 提出适合相应地区土壤水分反演的组合粗糙度参数S3 /L2 .因此,获取准确的地表粗糙度对于微波遥感反演土壤水分发挥着关键性作用. ...
被动微波遥感土壤水分
1
2012
... 土壤水分是农业、水文、土壤学、环境学等领域的重要参数.目前,利用空间分辨率较高的微波遥感对土壤水分进行实时、动态、高精度和大范围的反演是研究和应用的热点[3 -4 ] .在微波遥感领域,利用主动微波反演土壤水分所依赖的关键因子是后向散射系数,由于地表几何粗糙度对雷达后向散射系数具有显著的影响[5 -7 ] ,因此,几何粗糙度成为主动微波遥感领域研究的重点.同时,许多研究学者在被动微波反演土壤水分过程中发现了土壤水分与土壤粗糙度及其他关键因子之间的定量关系,从理论模型(IEM模型[8 ] 、AIEM模型[9 ] )到含有土壤粗糙度参数的半经验模型(Q/H模型[10 ] ).土壤水分反演算法中较为经典的半经验模型是Q/H模型,该模型包括极化混合因子Q,粗糙度参数H以及角度校正常数N等参数,但粗糙度效应的机理描述不够精确,改善对于粗糙度等关键影响参数的处理方法,是提高土壤水分产品质量的有效途径[10 -11 ] .近年来,组合(几何)粗糙度在反演土壤水分中应用广泛,Zhao等[12 ] 认为大多数自然土壤表面更接近指数相关地表,其发现使用几何粗糙度参数S2 /L能够很好地刻画粗糙度效应,并由此发展了参数化的土壤微波辐射模型;Lawrence等[13 ] 发现利用半经验模型Q/H反演到的粗糙度参数H与ZS =S2 /L和极化混合因子Q直接相关;Zribi等[14 ] 发现组合粗糙度S2 /L在雷达反演土壤水分中也具有较好的效果;陈晶等[15 ] 提出适合相应地区土壤水分反演的组合粗糙度参数S3 /L2 .因此,获取准确的地表粗糙度对于微波遥感反演土壤水分发挥着关键性作用. ...
被动微波遥感土壤水分
1
2012
... 土壤水分是农业、水文、土壤学、环境学等领域的重要参数.目前,利用空间分辨率较高的微波遥感对土壤水分进行实时、动态、高精度和大范围的反演是研究和应用的热点[3 -4 ] .在微波遥感领域,利用主动微波反演土壤水分所依赖的关键因子是后向散射系数,由于地表几何粗糙度对雷达后向散射系数具有显著的影响[5 -7 ] ,因此,几何粗糙度成为主动微波遥感领域研究的重点.同时,许多研究学者在被动微波反演土壤水分过程中发现了土壤水分与土壤粗糙度及其他关键因子之间的定量关系,从理论模型(IEM模型[8 ] 、AIEM模型[9 ] )到含有土壤粗糙度参数的半经验模型(Q/H模型[10 ] ).土壤水分反演算法中较为经典的半经验模型是Q/H模型,该模型包括极化混合因子Q,粗糙度参数H以及角度校正常数N等参数,但粗糙度效应的机理描述不够精确,改善对于粗糙度等关键影响参数的处理方法,是提高土壤水分产品质量的有效途径[10 -11 ] .近年来,组合(几何)粗糙度在反演土壤水分中应用广泛,Zhao等[12 ] 认为大多数自然土壤表面更接近指数相关地表,其发现使用几何粗糙度参数S2 /L能够很好地刻画粗糙度效应,并由此发展了参数化的土壤微波辐射模型;Lawrence等[13 ] 发现利用半经验模型Q/H反演到的粗糙度参数H与ZS =S2 /L和极化混合因子Q直接相关;Zribi等[14 ] 发现组合粗糙度S2 /L在雷达反演土壤水分中也具有较好的效果;陈晶等[15 ] 提出适合相应地区土壤水分反演的组合粗糙度参数S3 /L2 .因此,获取准确的地表粗糙度对于微波遥感反演土壤水分发挥着关键性作用. ...
Parametric Exponentially Correlated Surface Emission Model for L-band Passive Microwave Soil Moisture Retrieval
1
2015
... 土壤水分是农业、水文、土壤学、环境学等领域的重要参数.目前,利用空间分辨率较高的微波遥感对土壤水分进行实时、动态、高精度和大范围的反演是研究和应用的热点[3 -4 ] .在微波遥感领域,利用主动微波反演土壤水分所依赖的关键因子是后向散射系数,由于地表几何粗糙度对雷达后向散射系数具有显著的影响[5 -7 ] ,因此,几何粗糙度成为主动微波遥感领域研究的重点.同时,许多研究学者在被动微波反演土壤水分过程中发现了土壤水分与土壤粗糙度及其他关键因子之间的定量关系,从理论模型(IEM模型[8 ] 、AIEM模型[9 ] )到含有土壤粗糙度参数的半经验模型(Q/H模型[10 ] ).土壤水分反演算法中较为经典的半经验模型是Q/H模型,该模型包括极化混合因子Q,粗糙度参数H以及角度校正常数N等参数,但粗糙度效应的机理描述不够精确,改善对于粗糙度等关键影响参数的处理方法,是提高土壤水分产品质量的有效途径[10 -11 ] .近年来,组合(几何)粗糙度在反演土壤水分中应用广泛,Zhao等[12 ] 认为大多数自然土壤表面更接近指数相关地表,其发现使用几何粗糙度参数S2 /L能够很好地刻画粗糙度效应,并由此发展了参数化的土壤微波辐射模型;Lawrence等[13 ] 发现利用半经验模型Q/H反演到的粗糙度参数H与ZS =S2 /L和极化混合因子Q直接相关;Zribi等[14 ] 发现组合粗糙度S2 /L在雷达反演土壤水分中也具有较好的效果;陈晶等[15 ] 提出适合相应地区土壤水分反演的组合粗糙度参数S3 /L2 .因此,获取准确的地表粗糙度对于微波遥感反演土壤水分发挥着关键性作用. ...
Evaluating the Semiempirical H-Q Model Used to Calculate the L-band Emissivity of a Rough Bare Soil
1
2013
... 土壤水分是农业、水文、土壤学、环境学等领域的重要参数.目前,利用空间分辨率较高的微波遥感对土壤水分进行实时、动态、高精度和大范围的反演是研究和应用的热点[3 -4 ] .在微波遥感领域,利用主动微波反演土壤水分所依赖的关键因子是后向散射系数,由于地表几何粗糙度对雷达后向散射系数具有显著的影响[5 -7 ] ,因此,几何粗糙度成为主动微波遥感领域研究的重点.同时,许多研究学者在被动微波反演土壤水分过程中发现了土壤水分与土壤粗糙度及其他关键因子之间的定量关系,从理论模型(IEM模型[8 ] 、AIEM模型[9 ] )到含有土壤粗糙度参数的半经验模型(Q/H模型[10 ] ).土壤水分反演算法中较为经典的半经验模型是Q/H模型,该模型包括极化混合因子Q,粗糙度参数H以及角度校正常数N等参数,但粗糙度效应的机理描述不够精确,改善对于粗糙度等关键影响参数的处理方法,是提高土壤水分产品质量的有效途径[10 -11 ] .近年来,组合(几何)粗糙度在反演土壤水分中应用广泛,Zhao等[12 ] 认为大多数自然土壤表面更接近指数相关地表,其发现使用几何粗糙度参数S2 /L能够很好地刻画粗糙度效应,并由此发展了参数化的土壤微波辐射模型;Lawrence等[13 ] 发现利用半经验模型Q/H反演到的粗糙度参数H与ZS =S2 /L和极化混合因子Q直接相关;Zribi等[14 ] 发现组合粗糙度S2 /L在雷达反演土壤水分中也具有较好的效果;陈晶等[15 ] 提出适合相应地区土壤水分反演的组合粗糙度参数S3 /L2 .因此,获取准确的地表粗糙度对于微波遥感反演土壤水分发挥着关键性作用. ...
A New Empirical Model to Retrieve soil Moisture and Roughness from C-band Radar Data
1
2002
... 土壤水分是农业、水文、土壤学、环境学等领域的重要参数.目前,利用空间分辨率较高的微波遥感对土壤水分进行实时、动态、高精度和大范围的反演是研究和应用的热点[3 -4 ] .在微波遥感领域,利用主动微波反演土壤水分所依赖的关键因子是后向散射系数,由于地表几何粗糙度对雷达后向散射系数具有显著的影响[5 -7 ] ,因此,几何粗糙度成为主动微波遥感领域研究的重点.同时,许多研究学者在被动微波反演土壤水分过程中发现了土壤水分与土壤粗糙度及其他关键因子之间的定量关系,从理论模型(IEM模型[8 ] 、AIEM模型[9 ] )到含有土壤粗糙度参数的半经验模型(Q/H模型[10 ] ).土壤水分反演算法中较为经典的半经验模型是Q/H模型,该模型包括极化混合因子Q,粗糙度参数H以及角度校正常数N等参数,但粗糙度效应的机理描述不够精确,改善对于粗糙度等关键影响参数的处理方法,是提高土壤水分产品质量的有效途径[10 -11 ] .近年来,组合(几何)粗糙度在反演土壤水分中应用广泛,Zhao等[12 ] 认为大多数自然土壤表面更接近指数相关地表,其发现使用几何粗糙度参数S2 /L能够很好地刻画粗糙度效应,并由此发展了参数化的土壤微波辐射模型;Lawrence等[13 ] 发现利用半经验模型Q/H反演到的粗糙度参数H与ZS =S2 /L和极化混合因子Q直接相关;Zribi等[14 ] 发现组合粗糙度S2 /L在雷达反演土壤水分中也具有较好的效果;陈晶等[15 ] 提出适合相应地区土壤水分反演的组合粗糙度参数S3 /L2 .因此,获取准确的地表粗糙度对于微波遥感反演土壤水分发挥着关键性作用. ...
双极化雷达反演裸露地表土壤水分
1
2013
... 土壤水分是农业、水文、土壤学、环境学等领域的重要参数.目前,利用空间分辨率较高的微波遥感对土壤水分进行实时、动态、高精度和大范围的反演是研究和应用的热点[3 -4 ] .在微波遥感领域,利用主动微波反演土壤水分所依赖的关键因子是后向散射系数,由于地表几何粗糙度对雷达后向散射系数具有显著的影响[5 -7 ] ,因此,几何粗糙度成为主动微波遥感领域研究的重点.同时,许多研究学者在被动微波反演土壤水分过程中发现了土壤水分与土壤粗糙度及其他关键因子之间的定量关系,从理论模型(IEM模型[8 ] 、AIEM模型[9 ] )到含有土壤粗糙度参数的半经验模型(Q/H模型[10 ] ).土壤水分反演算法中较为经典的半经验模型是Q/H模型,该模型包括极化混合因子Q,粗糙度参数H以及角度校正常数N等参数,但粗糙度效应的机理描述不够精确,改善对于粗糙度等关键影响参数的处理方法,是提高土壤水分产品质量的有效途径[10 -11 ] .近年来,组合(几何)粗糙度在反演土壤水分中应用广泛,Zhao等[12 ] 认为大多数自然土壤表面更接近指数相关地表,其发现使用几何粗糙度参数S2 /L能够很好地刻画粗糙度效应,并由此发展了参数化的土壤微波辐射模型;Lawrence等[13 ] 发现利用半经验模型Q/H反演到的粗糙度参数H与ZS =S2 /L和极化混合因子Q直接相关;Zribi等[14 ] 发现组合粗糙度S2 /L在雷达反演土壤水分中也具有较好的效果;陈晶等[15 ] 提出适合相应地区土壤水分反演的组合粗糙度参数S3 /L2 .因此,获取准确的地表粗糙度对于微波遥感反演土壤水分发挥着关键性作用. ...
双极化雷达反演裸露地表土壤水分
1
2013
... 土壤水分是农业、水文、土壤学、环境学等领域的重要参数.目前,利用空间分辨率较高的微波遥感对土壤水分进行实时、动态、高精度和大范围的反演是研究和应用的热点[3 -4 ] .在微波遥感领域,利用主动微波反演土壤水分所依赖的关键因子是后向散射系数,由于地表几何粗糙度对雷达后向散射系数具有显著的影响[5 -7 ] ,因此,几何粗糙度成为主动微波遥感领域研究的重点.同时,许多研究学者在被动微波反演土壤水分过程中发现了土壤水分与土壤粗糙度及其他关键因子之间的定量关系,从理论模型(IEM模型[8 ] 、AIEM模型[9 ] )到含有土壤粗糙度参数的半经验模型(Q/H模型[10 ] ).土壤水分反演算法中较为经典的半经验模型是Q/H模型,该模型包括极化混合因子Q,粗糙度参数H以及角度校正常数N等参数,但粗糙度效应的机理描述不够精确,改善对于粗糙度等关键影响参数的处理方法,是提高土壤水分产品质量的有效途径[10 -11 ] .近年来,组合(几何)粗糙度在反演土壤水分中应用广泛,Zhao等[12 ] 认为大多数自然土壤表面更接近指数相关地表,其发现使用几何粗糙度参数S2 /L能够很好地刻画粗糙度效应,并由此发展了参数化的土壤微波辐射模型;Lawrence等[13 ] 发现利用半经验模型Q/H反演到的粗糙度参数H与ZS =S2 /L和极化混合因子Q直接相关;Zribi等[14 ] 发现组合粗糙度S2 /L在雷达反演土壤水分中也具有较好的效果;陈晶等[15 ] 提出适合相应地区土壤水分反演的组合粗糙度参数S3 /L2 .因此,获取准确的地表粗糙度对于微波遥感反演土壤水分发挥着关键性作用. ...
近景摄影测量提高裸露地表粗糙度测量精度
1
2017
... 测量粗糙度有多种不同的方法.针对不同的测量方式,地表粗糙度测量分为接触式测量和非接触式测量.接触式测量主要包括针板法、链条法和差分GPS等;常用的非接触式测量包括近景摄影测量法、激光扫描法、红外线传感器法和超声波测距法等[16 ] .目前,土壤表面粗糙度测量板方法(也称针板法)是遥感研究中普遍采用的土壤粗糙度测量方法,该装置构造较简易,尺寸适中,方便携带,适用于地表粗糙度的实地测量;通过拍摄获取土壤表面起伏的高度数据,采集成本低且便利,耗时短,测量效率高;由于测量针底端设有防护圆帽,测量针不会穿透地表插入土壤内部,避免了对土壤表面的破坏.针板法通过计算两个正交方向的均值以此反映整个研究样方的粗糙度. ...
近景摄影测量提高裸露地表粗糙度测量精度
1
2017
... 测量粗糙度有多种不同的方法.针对不同的测量方式,地表粗糙度测量分为接触式测量和非接触式测量.接触式测量主要包括针板法、链条法和差分GPS等;常用的非接触式测量包括近景摄影测量法、激光扫描法、红外线传感器法和超声波测距法等[16 ] .目前,土壤表面粗糙度测量板方法(也称针板法)是遥感研究中普遍采用的土壤粗糙度测量方法,该装置构造较简易,尺寸适中,方便携带,适用于地表粗糙度的实地测量;通过拍摄获取土壤表面起伏的高度数据,采集成本低且便利,耗时短,测量效率高;由于测量针底端设有防护圆帽,测量针不会穿透地表插入土壤内部,避免了对土壤表面的破坏.针板法通过计算两个正交方向的均值以此反映整个研究样方的粗糙度. ...
闪电河流域水循环和能量平衡遥感综合试验
1
2020
... 在闪电河流域水循环与能量平衡遥感综合试验[17 ] 中,与航空飞行试验同步进行了两个方向上的地表粗糙度测量,主要测量了闪电河流域南北航向以及东北西南航向中多个样方的地表粗糙度.其中,南北航线位于内蒙古自治区锡林郭勒盟正蓝旗县(115.990° E,42.241° N),河北省张家口市沽源县(115.688° E,41.669° N)所辖区域交界以及交界附近,东北—西南航线位于沽源县和承德市围场满族蒙古族自治县(117.761° E,41.938° N)所辖区域交界以及交界附近,如图1 所示.南北航向地域内地形复杂,典型地物种类繁多,具有草场、农用地、荒地、裸地和林地等具有代表性的地表覆盖种类,同一个大样方内不同地物类型所表现的地表起伏变化较大;东北西南航向地物类型简单,多为草地.试验期间共对61个不同地物类型的采样样方进行了粗糙度测量,南北航向的测量时间为2018年9月16日、17日,东南西北航向测量时间为2018年9月20日.其中草地采样样方19个,杂草地5个,胡萝卜地14个(其中未收割地10个,已收割4个),花菜地6个,玉米地4个(其中已收割3个,未收割1个),土豆地13个(已收割8个,未收割5个),如图1 所示. ...
闪电河流域水循环和能量平衡遥感综合试验
1
2020
... 在闪电河流域水循环与能量平衡遥感综合试验[17 ] 中,与航空飞行试验同步进行了两个方向上的地表粗糙度测量,主要测量了闪电河流域南北航向以及东北西南航向中多个样方的地表粗糙度.其中,南北航线位于内蒙古自治区锡林郭勒盟正蓝旗县(115.990° E,42.241° N),河北省张家口市沽源县(115.688° E,41.669° N)所辖区域交界以及交界附近,东北—西南航线位于沽源县和承德市围场满族蒙古族自治县(117.761° E,41.938° N)所辖区域交界以及交界附近,如图1 所示.南北航向地域内地形复杂,典型地物种类繁多,具有草场、农用地、荒地、裸地和林地等具有代表性的地表覆盖种类,同一个大样方内不同地物类型所表现的地表起伏变化较大;东北西南航向地物类型简单,多为草地.试验期间共对61个不同地物类型的采样样方进行了粗糙度测量,南北航向的测量时间为2018年9月16日、17日,东南西北航向测量时间为2018年9月20日.其中草地采样样方19个,杂草地5个,胡萝卜地14个(其中未收割地10个,已收割4个),花菜地6个,玉米地4个(其中已收割3个,未收割1个),土豆地13个(已收割8个,未收割5个),如图1 所示. ...
Fast Robust Perspective Transform Estimation for Automatic Image Registration in Disaster Response Applications
1
2012
... 拍取粗糙度照片过程中,因相机上下或者左右倾斜,导致粗糙度测量板无法正对相机光圈,易造成照片中粗糙度板呈现倾斜状态,倾斜的照片对后期数字化提取针头高度带来较大的高度误差,因而需要对照片做透视变换[18 -19 ] ,以此来校正拍照时角度倾斜的影响,透视变换实质是将图片投影到一个新的视平面[20 ] ,改变图像内部点的相对位置,使得已发生透视畸变的图像完成矫正的过程[21 ] .透视变换可降低在土壤粗糙度参数计算过程中因图像倾斜引起的偏差.透视变换涉及矩阵计算,为避免计算量过大,先将原始图片裁剪,裁剪区域包含整个粗糙度板,裁剪之后,确定源图像中粗糙度板白色底板的4个角点坐标,定义目标图中白色底板4个顶点坐标,利用两幅图像4个同名点的坐标求取变换矩阵,进行透视变换使得整个图片投影到粗糙度板白色底板所在平面.以2号样方的子样方1(草地)为例,图4 (a)为拍摄的原始照片,透视变换结果如图4 (b)所示.从图中可以明显看出透视变换前粗糙度测量板白色底板所在的二维平面明显不与图片所在平面平行,变换后可以看出变换的图片是测量板白色底板的正视图.通过变换将测量中粗糙度测量板白色底板正视图的倾斜角度进行了纠正. ...
Image Restoration Using Structured Sparse Representation with a Novel Parametric Data-Adaptive Transformation Matrix
1
2017
... 拍取粗糙度照片过程中,因相机上下或者左右倾斜,导致粗糙度测量板无法正对相机光圈,易造成照片中粗糙度板呈现倾斜状态,倾斜的照片对后期数字化提取针头高度带来较大的高度误差,因而需要对照片做透视变换[18 -19 ] ,以此来校正拍照时角度倾斜的影响,透视变换实质是将图片投影到一个新的视平面[20 ] ,改变图像内部点的相对位置,使得已发生透视畸变的图像完成矫正的过程[21 ] .透视变换可降低在土壤粗糙度参数计算过程中因图像倾斜引起的偏差.透视变换涉及矩阵计算,为避免计算量过大,先将原始图片裁剪,裁剪区域包含整个粗糙度板,裁剪之后,确定源图像中粗糙度板白色底板的4个角点坐标,定义目标图中白色底板4个顶点坐标,利用两幅图像4个同名点的坐标求取变换矩阵,进行透视变换使得整个图片投影到粗糙度板白色底板所在平面.以2号样方的子样方1(草地)为例,图4 (a)为拍摄的原始照片,透视变换结果如图4 (b)所示.从图中可以明显看出透视变换前粗糙度测量板白色底板所在的二维平面明显不与图片所在平面平行,变换后可以看出变换的图片是测量板白色底板的正视图.通过变换将测量中粗糙度测量板白色底板正视图的倾斜角度进行了纠正. ...
Research on Visualization Method of A-pillar Blind Zone based on 3D Reconstruction and Perspective Transformation
1
2019
... 拍取粗糙度照片过程中,因相机上下或者左右倾斜,导致粗糙度测量板无法正对相机光圈,易造成照片中粗糙度板呈现倾斜状态,倾斜的照片对后期数字化提取针头高度带来较大的高度误差,因而需要对照片做透视变换[18 -19 ] ,以此来校正拍照时角度倾斜的影响,透视变换实质是将图片投影到一个新的视平面[20 ] ,改变图像内部点的相对位置,使得已发生透视畸变的图像完成矫正的过程[21 ] .透视变换可降低在土壤粗糙度参数计算过程中因图像倾斜引起的偏差.透视变换涉及矩阵计算,为避免计算量过大,先将原始图片裁剪,裁剪区域包含整个粗糙度板,裁剪之后,确定源图像中粗糙度板白色底板的4个角点坐标,定义目标图中白色底板4个顶点坐标,利用两幅图像4个同名点的坐标求取变换矩阵,进行透视变换使得整个图片投影到粗糙度板白色底板所在平面.以2号样方的子样方1(草地)为例,图4 (a)为拍摄的原始照片,透视变换结果如图4 (b)所示.从图中可以明显看出透视变换前粗糙度测量板白色底板所在的二维平面明显不与图片所在平面平行,变换后可以看出变换的图片是测量板白色底板的正视图.通过变换将测量中粗糙度测量板白色底板正视图的倾斜角度进行了纠正. ...
图形变换中透视投影变换矩阵的推导
1
2003
... 拍取粗糙度照片过程中,因相机上下或者左右倾斜,导致粗糙度测量板无法正对相机光圈,易造成照片中粗糙度板呈现倾斜状态,倾斜的照片对后期数字化提取针头高度带来较大的高度误差,因而需要对照片做透视变换[18 -19 ] ,以此来校正拍照时角度倾斜的影响,透视变换实质是将图片投影到一个新的视平面[20 ] ,改变图像内部点的相对位置,使得已发生透视畸变的图像完成矫正的过程[21 ] .透视变换可降低在土壤粗糙度参数计算过程中因图像倾斜引起的偏差.透视变换涉及矩阵计算,为避免计算量过大,先将原始图片裁剪,裁剪区域包含整个粗糙度板,裁剪之后,确定源图像中粗糙度板白色底板的4个角点坐标,定义目标图中白色底板4个顶点坐标,利用两幅图像4个同名点的坐标求取变换矩阵,进行透视变换使得整个图片投影到粗糙度板白色底板所在平面.以2号样方的子样方1(草地)为例,图4 (a)为拍摄的原始照片,透视变换结果如图4 (b)所示.从图中可以明显看出透视变换前粗糙度测量板白色底板所在的二维平面明显不与图片所在平面平行,变换后可以看出变换的图片是测量板白色底板的正视图.通过变换将测量中粗糙度测量板白色底板正视图的倾斜角度进行了纠正. ...
图形变换中透视投影变换矩阵的推导
1
2003
... 拍取粗糙度照片过程中,因相机上下或者左右倾斜,导致粗糙度测量板无法正对相机光圈,易造成照片中粗糙度板呈现倾斜状态,倾斜的照片对后期数字化提取针头高度带来较大的高度误差,因而需要对照片做透视变换[18 -19 ] ,以此来校正拍照时角度倾斜的影响,透视变换实质是将图片投影到一个新的视平面[20 ] ,改变图像内部点的相对位置,使得已发生透视畸变的图像完成矫正的过程[21 ] .透视变换可降低在土壤粗糙度参数计算过程中因图像倾斜引起的偏差.透视变换涉及矩阵计算,为避免计算量过大,先将原始图片裁剪,裁剪区域包含整个粗糙度板,裁剪之后,确定源图像中粗糙度板白色底板的4个角点坐标,定义目标图中白色底板4个顶点坐标,利用两幅图像4个同名点的坐标求取变换矩阵,进行透视变换使得整个图片投影到粗糙度板白色底板所在平面.以2号样方的子样方1(草地)为例,图4 (a)为拍摄的原始照片,透视变换结果如图4 (b)所示.从图中可以明显看出透视变换前粗糙度测量板白色底板所在的二维平面明显不与图片所在平面平行,变换后可以看出变换的图片是测量板白色底板的正视图.通过变换将测量中粗糙度测量板白色底板正视图的倾斜角度进行了纠正. ...
Estimates of Surface Roughness Derived from Synthetic Aperture Radar(SAR) Data
1
1992
... 粗糙度参数是对地表凹凸状况的一种定量化表示.由于地表本身的各向异性,仅用一个参数无法将其特性进行合理化的表征,针对实际地表,往往利用多个参数进行粗糙度的刻画.同一地表根据角度不同定义了许多不同地表粗糙度相关参数,其中,基于地表廓线统计分析的传统粗糙度相关参数尤为经典.在微波遥感中通常用来表征地表粗糙度的参数有两类:一类是均方根高度S,用以刻画垂直方向上地表粗糙度;一类是自相关长度L,用来表征水平方向上的地表粗糙度状况 [22 -23 ] . ...
Erosion Process and Temporal Variations in the Soil Surface Roughness of Spoil Heaps under Multi-Day Rainfall Simulation
1
2020
... 粗糙度参数是对地表凹凸状况的一种定量化表示.由于地表本身的各向异性,仅用一个参数无法将其特性进行合理化的表征,针对实际地表,往往利用多个参数进行粗糙度的刻画.同一地表根据角度不同定义了许多不同地表粗糙度相关参数,其中,基于地表廓线统计分析的传统粗糙度相关参数尤为经典.在微波遥感中通常用来表征地表粗糙度的参数有两类:一类是均方根高度S,用以刻画垂直方向上地表粗糙度;一类是自相关长度L,用来表征水平方向上的地表粗糙度状况 [22 -23 ] . ...
Microwave Thermal Emission from Periodic Surfaces
1
2007
... 作物区地表粗糙度不仅与数据倾斜密切相关,同时也受周期性田垄结构的影响,周期性田垄结构具有各向异性,在垂直垄向方向上,表面粗糙度受大尺度垄结构特性影响,而在平行垄方向上,表面粗糙度主要受表面的小尺度起伏影响.如果不进行周期性校正,表面粗糙度参数的各向异性会非常严重.研究表明周期性表面计算的地表粗糙度会导致模拟的雷达后向散射系数或者被动微波亮温产生误差[24 ] .去除周期性田垄结构的影响,有利于提高作物区地表粗糙度的精度[25 ] .周期校正采用的方法是首先对数字化的测量数据进行最小二乘拟合获取最佳拟合曲线,并记录下最佳拟合曲线上与测量数据相对应的拟合值,利用数字化的测量数据与拟合数据的差值获取作物区去除田垄结构影响的用于计算地表粗糙度参数的地表高度数据.对于包含人为因素的复杂地表(如农田),仅进行倾斜校正并不能满足其精度要求,须对数据作进一步处理分析. ...
农田表面粗糙度参数的测量与精度分析
1
2013
... 作物区地表粗糙度不仅与数据倾斜密切相关,同时也受周期性田垄结构的影响,周期性田垄结构具有各向异性,在垂直垄向方向上,表面粗糙度受大尺度垄结构特性影响,而在平行垄方向上,表面粗糙度主要受表面的小尺度起伏影响.如果不进行周期性校正,表面粗糙度参数的各向异性会非常严重.研究表明周期性表面计算的地表粗糙度会导致模拟的雷达后向散射系数或者被动微波亮温产生误差[24 ] .去除周期性田垄结构的影响,有利于提高作物区地表粗糙度的精度[25 ] .周期校正采用的方法是首先对数字化的测量数据进行最小二乘拟合获取最佳拟合曲线,并记录下最佳拟合曲线上与测量数据相对应的拟合值,利用数字化的测量数据与拟合数据的差值获取作物区去除田垄结构影响的用于计算地表粗糙度参数的地表高度数据.对于包含人为因素的复杂地表(如农田),仅进行倾斜校正并不能满足其精度要求,须对数据作进一步处理分析. ...
农田表面粗糙度参数的测量与精度分析
1
2013
... 作物区地表粗糙度不仅与数据倾斜密切相关,同时也受周期性田垄结构的影响,周期性田垄结构具有各向异性,在垂直垄向方向上,表面粗糙度受大尺度垄结构特性影响,而在平行垄方向上,表面粗糙度主要受表面的小尺度起伏影响.如果不进行周期性校正,表面粗糙度参数的各向异性会非常严重.研究表明周期性表面计算的地表粗糙度会导致模拟的雷达后向散射系数或者被动微波亮温产生误差[24 ] .去除周期性田垄结构的影响,有利于提高作物区地表粗糙度的精度[25 ] .周期校正采用的方法是首先对数字化的测量数据进行最小二乘拟合获取最佳拟合曲线,并记录下最佳拟合曲线上与测量数据相对应的拟合值,利用数字化的测量数据与拟合数据的差值获取作物区去除田垄结构影响的用于计算地表粗糙度参数的地表高度数据.对于包含人为因素的复杂地表(如农田),仅进行倾斜校正并不能满足其精度要求,须对数据作进一步处理分析. ...
Comparison of Two Bare-soil Reflectivity Models and Validation with L-band Radiometer Measurements
1
2010
... 在计算相关长度过程中,常用表面自相关函数来描述随机地表在水平距离上两个点的高度之间的自相关程度.在理论模型中,土壤表面的自相关函数通常有高斯相关、指数相关和1.5倍功率自相关3种.在计算获取实际测量样方地表的相关函数时,将已经计算得到的相关长度值代入高斯、指数相关函数,首先获得理论上的自相关曲线,然后将计算得到的样方地表的自相关函数曲线与理论的自相关函数曲线进行对比,计算的自相关函数曲线与哪种理论的曲线更接近,就取该种自相关函数作为该土壤表面的自相关函数类型.根据自相关函数的计算结果分析,具有田垄结构的农作物样方(土豆地、花菜地、胡萝卜地和玉米地)平行于垄方向地势起伏较小,自相关函数多为指数相关,垂直于垄方向由于田垄的存在,使得地表变得粗糙,其自相关函数多为高斯相关.其中,6个花菜地采样样方中的4个,13个土豆地采样样方中的9个,14个胡萝卜地采样样方中的7个,4个玉米地采样样方中的2个都具有在平行垄方向为指数相关函数,垂直垄方向为高斯相关函数的规律.在其他不满足这种规律的采样样方中,自相关函数多为指数相关.对于没有明显田垄结构的草地和杂草地,地势平坦,地表相对光滑,自相关函数多为指数相关,其中19个草地的采样样方中有15个为指数相关,5个杂草地采样样方中有4个为指数相关.因此,根据计算结果分析可以得出,平滑地表接近指数自相关函数,粗糙地表更接近高斯自相关函数.对于普通的自然地表,指数相关能更好的模拟其随机变化,这与前人的研究具有很好的一致性[26 ] . ...