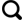来自多源遥感卫星数据的植被指数时间序列数据集在土地利用类型分类^［1-2］、植被活动监测^［3-4］、物候信息提取^［5-6］等领域有着非常广泛的应用，因此它早已经成为了许多科学研究、工程项目的重要数据源之一^［7］。然而云、云阴影、大气溶胶、冰雪、视场、数据传输等都会污染遥感植被指数^［8］。为了解决这些问题，虽然研究者已经开发了许多处理方法，并将最大值合成^［9］（Maximum Value Composite，MVC）应用到了数据集的生产中，但是最终生成的数据集仍会受到云、云影等的影响，研究人员仍需要在众多数据中筛选出合适无云影像，这限制了数据的进一步应用。因此，寻找一种可靠的重建算法来处理影像非常重要。

目前，国内外运用比较广泛的方法有HANTS^［10］（Harmonic Analysis of NDVI Time Series）、S-G滤波^［11］（Savitzky-Golay Filter， S-G）、非对称高斯拟合法^［12］（Asymmetric Gaussian model function， AG）、双逻辑拟合法^［13］（Double Logistic function， DL）。Per Jönsson和Lars Eklundh开发的TIMESAT软件集成了S-G、AG、DL 3种算法，且该软件运用广泛，尤以S-G算法运用最多且效果良好^{［11， 14-16］}。从2004年Chen等^［11］用迭代的S-G算法对NDVI序列进行滤波开始，到2012年张慧芳等^［17］的基于背景库的时序数据S-G滤波重建，再到2013和2019年周增光等^［18-20］结合影像质量的S-G滤波等，基于S-G滤波的重建算法取得了很大进展。然而，这些方法都在追求时间序列曲线的上包络线，容易出现过拟合的现象。实验结合克里金插值方法和质量权重，最大限度地保留了可靠像元，减少过拟合现象的出现。利用皮尔逊相关系数和新的平滑度指数进行对比，找出重庆市范围内二者表现都较好的SG滤波算法参数组合。

此外，大范围的长时间序列数据带来了数据量的激增，使用传统的本地环境和数据进行恢复重建会造成大量的数据冗余和时间浪费。而GEE是谷歌建立的一款云计算平台，可以直接在线处理Landsat、MODIS、Sentinel等卫星影像数据及其衍生数据集。目前，很多人已经使用这个平台来处理和分析数据，并取得了很多的成果^［21-25］。因此，在带有大型数据库的云计算平台上处理和分析遥感影像已经成为一种新的趋势。但目前重建算法还没有在GEE平台上得到有效的应用。

重庆地处西南，跨28°10′~32°13′N，105°11′~ 110°11′E，面积达8.24万km²，年日照数1 000~1 500 h，日照率仅为25%~35%；其中冬春季日照更少，多为云雾天气。中西部为低山丘陵地带、东南部海拔较高为多山峰、东北部为高峡平湖，导致东南部与中西部全年云量较多，而东北部云量较少。因此对该地区植被指数长时间序列进行恢复重建，具有良好的现实意义。

实验数据源为MODIS全球数据集：MOD13Q1.006（https：//lpdaac.usgs.gov/products/mod13q1v006/），其时间分辨率为16 d、空间分辨率为250 m。选取2014年立春至2018年冬末（2014-03-22~2019-03-21），每年23景，共计115景。使用了MOD13Q1.006中的NDVI以及DetailedQA两个波段。其中NDVI值以16位有符号整型方式存储，范围从-2 000到10 000，运用式（1）可求得所需NDVI值。

DetailedQA以16位无符号整型方式存储，在比特位0~1处为指数质量指标，具体如表1所示。

实验结合数据集的质量波段信息与空间插值和S-G滤波提出一种新方法（Weight-SG，WSG）从时空上均对被污染的像元值进行恢复重建。具体算法流程如图1所示。

首先对时间段内的全球影像进行裁剪，仅保留重庆区域；同时统计影像质量波段信息，得出各质量等级占比后再转化为相应的质量权重。然后利用克里金插值法对原始影像进行空间插值，并按其权重对插值结果与原始影像进行合成同时更新权重；接着继续进行S-G滤波重建，再次结合质量权重得出最终的影像。

S-G滤波算法基于假设^［26］（云、气溶胶等对NDVI值的影响往往倾向削弱NDVI值的方向）进行迭代来逼近原始NDVI曲线的上包络线从而获得最终结果。但在实际过程中并不完全满足该假设：在低NDVI值的背景区域，NDVI值反而会有所升高，所以盲目的取较大值并不可取。实验结合像元本身的质量等级为其分配不同的权重，继而获得最终的结果如式（2）所示。

其中：NDVIi*表示最终值；NDVIi表示该像元处理前的值；wi表示该像元质量的权重；NDVIi'表示该像元通过空间插值或滤波之后得到的拟合值。

Tobler地理学第一定律^［26］指出：任何事物与别的事物之间都是相关的，但近处的事物比远处的事物的相关性更强。S-G滤波不能对不同时间间隔的数据进行处理，所以在进行滤波重建之前对数据进行适当的插值不仅能方便进一步的处理，也能极大的提高中、低质量和噪声像元的可信度。

克里金插值法^［27］（Kriging/Krige）最早是由法国地理学家Matheron和南非矿山工程师Krige提出的，主要用于矿山勘探。克里金插值法认为在空间中属性的变化是非常不规则，且不连续的，用简单的平滑函数将出现较多的误差，应该使用能反应空间变异性的变异函数。具体公式如式（3）所示：

其中：Zx0,y0是n个采样点值的加权和；Z(xi,yi)是采样点(xi,yi)处的值；λi(i=1,2,···,n)为代求权系数由变异函数确定。不同的变异函数拟合模型适用于不同的空间环境，常见的变异函数包括指数模型（Exponential）、高斯模型（Gaussian）以及球形模型（Spherical）等。重庆市多山地，地表覆盖类型变化较快，空间自相关性在一定距离范围内消失的也较快，且该距离范围也相对较小，所以使用球型模型更加合适。变异函数模型有3个参数：range是模型的变程，即插值结果的有效范围；sill是基台值，即超出范围后的恒定方差；nugget是块金值，即距离为0是的半方差值。重庆市土地覆盖类型变化较快所以在实验中三者分别设置为：500、1.0和0.1。

重庆市影像质量较差，使用部分像元进行小范围插值时会导致其它区域没有插值结果，因此实验中对全图使用了克里金插值，同时为了减少中、低质量像元对插值结果的影像，在插值后引入质量权重占比对结果进行再次处理。原始影像中高质量像元的值直接代替插值结果，而中、低质量像元按照权重占比来重新合成。同时对结果的质量进行新一轮判定，并在之后的SG滤波中沿用该等级。

S-G滤波是由Savizky和Golay率先提出继而广泛应用于平滑时间序列数据的算法^［11］。S-G滤波是一种基于最小二乘法多项式拟合法，通过一定长度的窗口大小，对待处理数据进行多项式加权拟合，继而求出最小均方根误差。其基本公式如式（4）所示：

其中：N为窗口大小，满足N=2m+1；Cj表示S-G多项式拟合的系数。S-G滤波有两个参数：m是半窗大小，d是拟合的多项式项数。在陈晋等^［11］提出的SG滤波中，通过实验指出m的推荐取值范围为2~7，d的取值范围为2~4。实验提出的WSG算法滤波过程中使用的并非是和S-G滤波算法一样的原始遥感影像，而是空间插值结合质量权重后的影像；同时对滤波重建后的结果再次结合质量权重确保尽最大可能保留高质量像元值，而仅拟合中、低质量及噪声的像元NDVI值。

Pearson相关系数是一种常见的统计学系数，用来表示两组变量的相关程度。具体如式（5）所示：

其中：cov(X,Y)是变量之间的协方差；ρXρY是标准差。实验中，用来计算样本点重建前后的相关程度。平滑度是本实验新提出的一种用于评价曲线平滑程度的指标，在时间序列曲线上，锯齿越大越多，曲线就越粗糙，NDVI值产生波动的范围也越大，且产生这种大范围波动的频率也就越高。锯齿在折线图中和极值类似，通过统计该段曲线内极值点的个数可以描述曲线的平滑程度S。在研究区域内，大体为单生长季植物，即在理想情况下：NDVI值从一年的春季开始单调递增，夏季达到最大之后再单调递减，一年内有3个极值点；若为双生长季植物，则一年内有2个波峰3个波谷，即5个极值点。综上所述，定义平滑度S如式（6）所示。

其中：M为极值点个数；y为曲线所跨越的时间长度（按年计）；n为当地所生长植被的生长季个数；N为数据集每年的影像总数。

为了进一步比较S-G滤波算法以及WSG算法的重建结果，选取2014年春到2018年冬末影像质量较好的5幅，对原始影像引入10%的随机噪声，再对新的数据集分别进行S-G和WSG滤波。由于原始影像的质量较好，所以可以将原始影像作为参考影像，对比两种方法重建后的相关性以及噪声区域的NDVI值变化，可以定量分析重建结果。

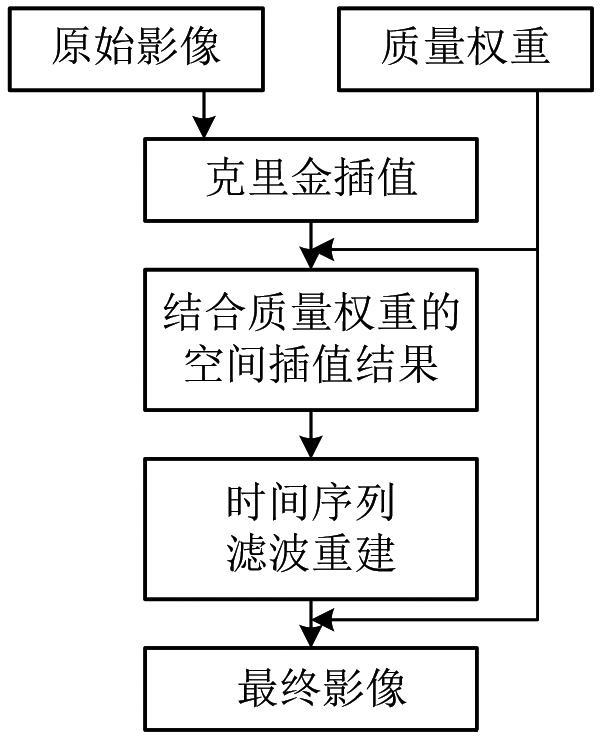
利用MOD13Q1自带的指数质量波段，对5 a内的图像进行分析，如图2所示。结果表明：5 a内中质量像元占比数量最多达到了40.67%，而高质量和低质量像元分别占比30.36%和28.95%，噪声像元仅占0.02%。2018年冬季高质量像元占比最低，仅为4.78%；2017年春季高质量像元占比最高，为61.82%。整体呈现出春夏季节高质量数据多而秋冬季节的低质量数据多的特征，从春季开始高质量数据占比逐减降低直到冬季达到最低。其中2014年春季质量高的像元占比较少，和上文提到的情况有所出入，详细浏览数据发现是由于该时间段内卫星数据缺失严重所引起的。

从整体上看中质量像元占比在40.67%，低质量像元占比在28.95%；所以将质量权重分别设置为0.4和0.3，具体的质量等级与权重转换表如表2所示。

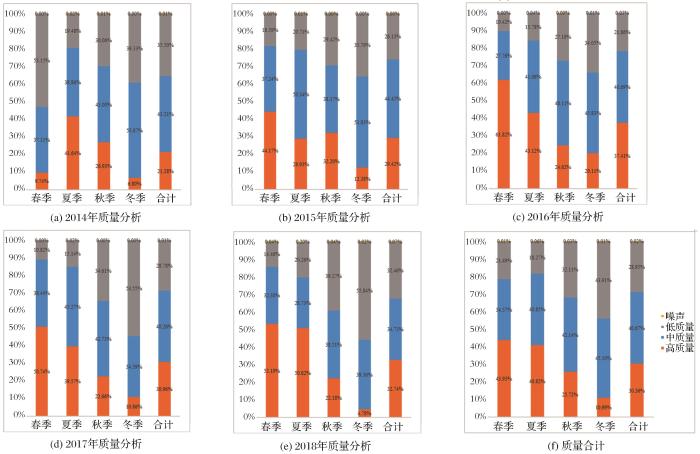
为了降低中、低质量与噪声像元对滤波重建结果的影响，实验使用空间插值法对图像进行处理来填充缺失值，提高像元的可信度，并选取时间段内第一幅影像（时间：2014年3月22日）来说明插值结果。

插值后的结果如图3所示。图3（a）是原始图像，重庆东南部、中西部的NDVI值较低，整体受云雾影响较为严重。图3（b）是克里金插值后的影像，云污染区域面积有所减少，但大面积污染区域中心NDVI值仍旧较低；另外，插值后的结果有明显的块效应和边缘断层现象。而结合了质量权重的空间插值如图3（c）所示，相较于图3（b）块效应有所减少。

从图3可以看到，对中低质量像元进行插值后的影像部分区域仍旧污染严重，以重庆主城区为例，如图4所示。

对图4（a）进行目视解译可知：蜿蜒的白色区域为长江、嘉陵江交汇处，周围橙色区域为主城区。图4（b）、图4（c）都能保持主城区的大概轮廓，但图4（c）比图4（b）保留了更多细节，图4（b）具有较为严重的块效应，但图4（c）没有。小范围区域内，图4（b）更倾向于同质化，而图4（c）的NDVI值变化更加丰富，但仍是较为均匀的。如图5所示，是使用克里金插值法处理原始图像后各等级质量像元的分布情况。

原始影像中，高质量和噪声像元较少，中、低质量像元较多。而经过插值处理后的质量图5（b）：高质量像元有少量增加，中质量像元大幅减少，低质量像元略有增加，噪声像元也大幅增加；图5（c）与图5（b）变化情况相同，仅在变化幅度上有所差异。通过插值可以重建部分云污染区域，但仍有像元需要进一步处理。所以对插值后的影像进行滤波，从时间维度上提取更多的信息进行重建是有必要的。

S-G算法半窗大小m一般取值范围在2~7、多项式项数d在2~4。为了探寻不同参数组合的S-G滤波在重庆市范围的不同结果，实验对图6所示的50个随机样本点，以及18种参数组合，做了共计900组实验。选取不同影像质量不同程度的3个样本点进行说明，如图6中红点所示：其中样本点17位于重庆东南部，影像质量一般，样本点26位于西部影像质量较差，样本点39位于东北部影像质量较好。

S-G滤波结果的NDVI曲线相关性均值为0.77、平滑度均值为0.75，其中结果高于相关性均值的实验有496组，高于平滑度均值的实验有459组，高于均值的实验参数分布情况如表3所示。

由结果分析可知：随着m的增加，相关性越低、平滑度越高；随着d的增加，相关性越高、平滑度越低。所以本实验将后续的S-G滤波以及WSG滤波参数m、d均设置为5和3。

对5 a内的数据进行滤波后，结果如图7所示。样本点的时间序列曲线能直观反映各样本点的影像质量：样本点17，波动较大、但产生大波动的频率不如样本点26；样本点26波动小于17，但产生大波动的频率远远高于17；而样本点39大波动较少，频率也较低。完全符合选取的样本点实际情况。3个样本点中，S-G方法均存在一定程度上的低估或高估，为了平滑丢失了部分细节，虽然平滑度较高，但相关性很低。尤其以样本点26最为严重，因为影像波动过于频繁，导致拟合值与原始值差距较大。而WSG方法虽然平滑度不如S-G但高于原始曲线，且WSG相关性高于S-G。即WSG方法的相关性很高，对原始NDVI序列的改变较小；S-G滤波结果具有一定的过拟合现象。具体3个样本点的对比如表4所示。

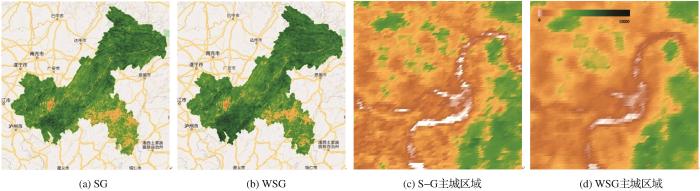
依旧选取时间段内第一幅影像进行说明，图8（a）、图8（b）分别是SG滤波和WSG滤波结果，与图3（a）的原始影像相比二者都重建了较大范围，但WSG滤波比S-G保留了更多的细节，且没有出现明显的过拟合现象。虽然从直观上S-G滤波结果看起来更好，植被区域更广阔，但是其与原始影像的相关系数仅为0.62，数据的可信度大大降低，并且低NDVI值的建筑区域存在较为严重的过拟合现象；而WSG结果的相关系数为0.78，比S-G滤波更加贴近实际情况。图8（c）、图8（d）分别是其对应的主城区，S-G滤波结果更复杂，在同一地物的建筑区域，NDVI变化频繁，且范围过大不符合实际情况，但河流的轮廓比WSG清晰一些；WSG滤波结果在建筑区域，NDVI变化更加均匀，恢复结果略好于S-G。

实验选取2016年5月24日与2017年4月7日两幅影像来进行说明，两幅原始影像添加了10%的随机噪声后如图9所示。

通过S-G滤波以及WSG滤波后的结果如图10所示：从直观上来讲，WSG重建后的结果比S-G更好，有效的重建了噪声区域的NDVI值。而S-G的重建结果整体NDVI值偏高较为严重，且能明显的观察到噪声像元存在过的痕迹。对二者进行相关性分析，S-G的Pearson相关系数分别为0.65和0.61，而WSG为0.87和0.94明显高于S-G的相关性，重建结果在目视上也更接近于真实影像。

为了更直观地展示重建结果，对比原始影像和重建影像中噪声部分的NDVI值变化，具体如图11所示（为方便展示，NDVI均乘以一万）。

由图11可以明显看出，在人为添加的噪声区域中，WSG重建结果与真实影像更加接近，差值集中在在1 000以内，少部分在1 000~2 000，超过3 000的很少；而S-G重建结果相对较差，大部分在1 000~3 000，最大值甚至接近6 000。所以，整体来讲，WSG方法的恢复重建效果优于S-G。

实验基于GEE云平台实现了经典S-G滤波算法，并在其基础上，结合空间插值法和质量权重提出了WSG方法，进一步在参数不变的情况下提升了重建结果的相关性。同时提出了一个平滑度指标来描述时间序列曲线的平滑程度。通过对研究结果进行分析主要得出以下结论：

（1）使用空间插值法对原始影像中的低质量及噪声像元进行预处理后，能够提升滤波重建结果的相关性，但要尽量减小因插值带来的块效应。S-G滤波算法和WSG都能够较好地重建被云雾覆盖等原因污染的NDVI值，同参数下S-G滤波在相关性上低于WSG，在平滑度上略高于WSG。

（2）GEE云平台能够完成一部分的空间信息处理与分析工作，降低了遥感信息处理的门槛，但相较于传统工具（ArcGIS、QGIS、ENVI等）还有一定的差距。本研究使用时遇到的主要问题体现在：①分配给用户的云计算资源略有不足；②没有较为完善的制图、出图工具；③基于C/S架构，用户运行的结果往往是异步的，如果使用较多的循环等会导致运行超时网页无响应；④对矢量文件的运算处理缺少优化，计算复杂边界时会导致运算量加大。

时间序列数据重建对于生成更加可靠的数据，进行下一步研究具有重大意义，结合云计算可以在减少数据收集、预处理时间的同时加快重建算法的运行效率。且随着越来越多的科研人员加入与技术的逐步发展，时间序列重建甚至可以在做到与原始数据一样的更新频率的情况下获得质量更好的影响，为后续的土地利用类型分类、植被覆盖度分析等奠定良好的基础。