遥感技术与应用, 2020, 35(2): 458-468 doi: 10.11873/j.issn.1004-0323.2020.2.0458

遥感应用

基于相对光谱变量的无人机遥感水稻估产及产量制图

王飞龙,1, 王福民,2, 胡景辉2, 谢莉莉2, 谢京凯1

1.浙江大学建筑工程学院，浙江 杭州 310058

2.浙江大学环境与资源学院，浙江 杭州 310058

Estimating and Mapping Rice Yield Using UAV-Hyperspectral Imager based Relative Spectral Variates

Wang Feilong,1, Wang Fumin,2, Hu Jinghui2, Xie Lili2, Xie Jingkai1

1.Institute of Hydrology and Water Resources, College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China

2.Institute of Remote Sensing and Information Technology Application, College of Environment and Resource Science, Zhejiang University, Hangzhou 310058, China

通讯作者: 王福民（1978-），男，山东高密人，副教授，主要从事无人机遥感、资源环境遥感模型方面的研究。E⁃mail：wfm@zju.edu.cn

收稿日期: 2018-10-15   修回日期: 2020-01-16   网络出版日期: 2020-06-19

基金资助: 国家重点研发计划.  2016YFD0300601
国家自然科学基金项目.  41871328
浙江省微波目标特性测量与遥感重点实验室开放基金.  2018KF02

Received: 2018-10-15   Revised: 2020-01-16   Online: 2020-06-19

作者简介 About authors

王飞龙（1994-），男，河南洛阳人，硕士研究生，主要从事水文与水资源、遥感应用方面的研究E⁃mail：wangfeilong@zju.edu.cn , E-mail：wangfeilong@zju.edu.cn

摘要

及时准确地监测农作物产量信息对国家和区域的粮食生产、贸易及粮食安全预警具有重要意义。当前卫星遥感估产由于高时空分辨率难以同时满足、波段数量少等原因限制估产精度进一步提高，无人机成像高光谱技术以其高时空分辨率、丰富的波段数量和图谱结合的遥感影像等优势被广泛地应用到现代智慧农业与精准农业，使高精度的农作物估产成为了可能。常规无人机估产方法使用的不同时期植被指数在获取时具有不同的光照条件、大气条件和背景，这些外界条件的差异将会引起不同时期植被指数的误差，进而影响估产精度。针对该问题，提出“相对光谱变量”和“相对产量”的概念开展多时期相对变量水稻遥感估产。首先将高光谱成像仪获取的波段进行一对一的组合建立相对归一化光谱指数RNDSI集，并确定水稻不同生育期的最优RNDSI及其构成波段；然后建立不同生育期组合的水稻估产最优模型并做相应的验证。结果显示:使用分蘖期RNDSI[784,635]、拔节期RNDSI[807,744]、孕穗期RNDSI[784,712]和抽穗期RNDSI[816,736]组成的多元线性回归模型是多生育期估产的最优模型，R2和RMSE分别为0.74和248.97 kg/hm2，并对此结果进行验证，估产平均相对误差绝对值达到了4.31%，结果表明相对植被指数和相对产量的水稻遥感估产方法可较好地应用于像素级的水稻遥感估产。基于该模型绘制了水稻的田间产量分布图，可更加直观地表现不同区域的产量并进行精准地田间管理。关 键 词：无人机;成像高光谱;相对光谱变量;水稻;估产;空间分布

关键词： 无人机 ; 成像高光谱 ; 相对光谱变量 ; 水稻 ; 估产 ; 空间分布

Abstract

Crop yield is important for national and regional food production, food trade and food security. Traditional yield estimation by satellite remote sensing is limited by many factors such as spatiotemporal resolution and number of bands. UAV imaging hyperspectral technology has been widely applied to modern intelligent agriculture and precision agriculture with its advantages of high spatial and temporal resolution, rich band number and the combination of image and spectrum It is possible to estimate crop yield accurately. The multi-temporal vegetation indices for yield estimation are obtained with different illumination conditions, atmospheric conditions and background values, the differences in these external conditions may result in errors in vegetation indices. Therefore, using these multi-temporal vegetation indices which containing these external conditions for yield estimation is likely to cause errors. To address this problem, this study proposes the concept of “relative spectral variables” and “relative yield” to estimate rice yield using multi- temporal relative variables. Firstly, the bands obtained from hyperspectral imager are combined to establish the Relative Normalized Difference Spectral Index(RNDSI) and the optimal RNDSI are selected for different growth stages. Then, the optimal models of rice yield estimation with different growth stage combinations are determined and validated. The results shows that multiple linear regression model consisting of tillering stage RNDSI[784, 635], jointing stage RNDSI[807, 744], booting stage RNDSI[784, 712] and heading stage RNDSI[816, 736] is the optimal models for rice yield estimation with R2 of 0.74 and RMSE of 248.97 kg/ha. This model is validated and the result is acceptable with average relative error of 4.31%. In conclusions, the relative vegetation index and relative yield can be applied to the pixel-level yield estimation by remote sensing. Besides, the rice yield distribution map is drawn based on the model, which represents the differences of rice yield at different filed positions. The map may be used to carry out precise field management.

Keywords： UAV ; Imagery hyperspectral ; Relative spectral variable ; Rice ; Yield estimation ; Spatial distribution

PDF (4029KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

王飞龙, 王福民, 胡景辉, 谢莉莉, 谢京凯. 基于相对光谱变量的无人机遥感水稻估产及产量制图. 遥感技术与应用[J], 2020, 35(2): 458-468 doi:10.11873/j.issn.1004-0323.2020.2.0458

Wang Feilong, Wang Fumin, Hu Jinghui, Xie Lili, Xie Jingkai. Estimating and Mapping Rice Yield Using UAV-Hyperspectral Imager based Relative Spectral Variates. Remote Sensing Technology and Application[J], 2020, 35(2): 458-468 doi:10.11873/j.issn.1004-0323.2020.2.0458

1 引 言

古往今来，足食是治国安邦的首善大举。中国作为拥有13.7亿人口[1]的世界上最大发展中国家，粮食安全一直是“天字第一号”问题。粮食供给的稳定与社会经济的发展密切相关，粮食生产安全历来也是党和政府高度重视的问题，并且提出了“确保谷物基本自给、口粮绝对安全”的战略底线，以确保国家粮食安全。水稻是中国最重要也是种植最广泛的粮食作物之一[2]，2015年其种植面积和产量分别占粮食作物的种植面积和产量的26.7%和33.5%[3]。在当今复杂多变条件下，精准的水稻产量信息获取对于国家粮食安全、农业政策的制定、国家粮食价格的调控、水资源的合理调配具有重要的指导意义[4]。

农业遥感技术具有非破坏性、非接触性、快速高效和低成本的优势被广泛地应用到了农业估产工作当中并取得了丰硕的成果[5]。传统的卫星遥感具有大区域监测的优势，但由于高时空分辨率难以同时满足、波段数量少等因素已经无法满足现代园区精准农业、智慧农业的需要。无人机遥感以其灵活、高通量等特性能够按需获取高空间分辨率的数据，提供近实时的遥感影像在精准农业领域得到了广泛应用。尤其是近年来无人机和高光谱成像技术的日益成熟，其能够在低空获得分辨率达到1cm的超高分辨率影像使得作物的精准监测成为了可能[6]。传感器作为无人机遥感平台的核心，经历了彩色数码相机、近红外相机、多光谱相机到高光谱相机的发展过程，前3类传感器由于波段数量的限制不能依据生育期变化在不同生长阶段获取不同的敏感波段数据，成像高光谱相机以其更多的光谱波段、精细的光谱信息和图谱结合等优势逐渐成为无人机遥感的热门研究方向。已有研究人员利用无人机高光谱遥感影像反演冬小麦叶面积指数[7]，预测大豆育种产量[8]，评估小麦地表生物量[9]，监测橄榄树黄萎病等[10]，均取得了良好的结果，但在水稻估产方面的研究较少。

无人机遥感平台虽然不受时空分辨率的限制可广泛地应用到精准农业当中去，但存在一些问题需要进一步研究。例如对于无人机遥感来说，通常采用标准的参考白板或灰板计算不同日期的反射率，再计算各种光谱指数开展监测[11,12]。但是由于受到不同时期大气条件、光照条件差异的影响，尽管利用这些伪不变地物[13]或不同反射率标准反射板校正法能够一定程度地减弱由于不同时期遥感观测条件差异引起的影响，但校正结果仍然存在一些不确定性，难以获取绝对准确的反射率[14]。常用遥感估产方法是建立多个生育期植被指数与产量之间的统计模型，该方法由于具有简单、高效等优点而被广为应用[15,16,17,18]。但由于多个时期植被指数是在不同外界条件下获取的，不同时期反射率计算的植被指数所包含的误差必然会引起估产精度的下降。事实上，绝对准确的遥感变量是很难获得的，遥感变量的相对变化更能反映出同一观测条件下作物的生长状态的差别，为此，本研究依据同一时期不同田块之间遥感变量具有相同的辐射、大气、太阳高度角等外界条件和相似的背景条件，尝试通过利用这些同一条件下获得的遥感变量构建相对光谱变量的方法减弱各种外界的影响，进一步开展基于多生育期相对光谱变量的水稻估产研究。本研究目的在于:①建立一种利用相对光谱变量的水稻估产方法，该方法能够一定程度上消除大气条件、光照条件差异以及稻田背景对真实反射率的影响；②充分利用成像高光谱数据的波段优势确定水稻估产的最优波段组合；③确定水稻估产的最佳生育期组合；④绘制产量分布图，分析产量的空间分布特征。

2 数据与方法

2.1　研究区概况

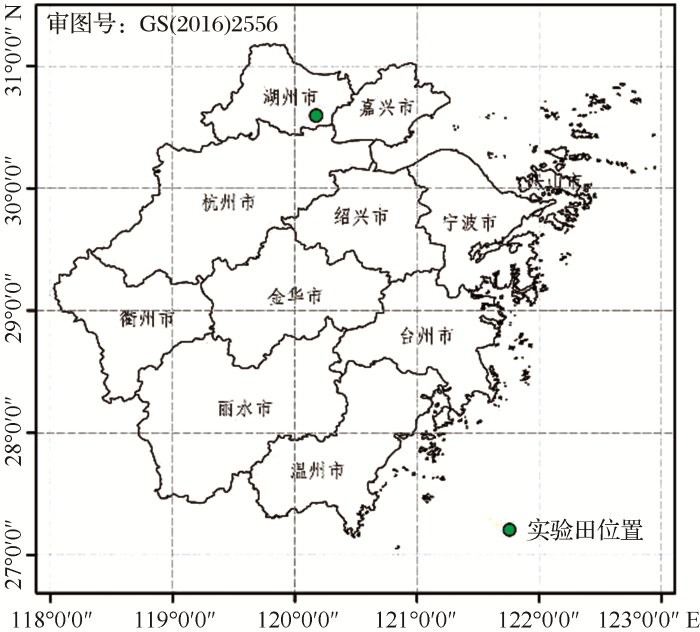
实验区域位于浙江省湖州市德清县新安镇下舍村省级粮食生产功能区，地理位置为120°10'49.34" E，30°34'21.21" N，海拔高度5 m(图1)。实验区东西总长101 m，南北总长81 m，区内包含有两个水稻品种嘉-58(V1)和浙粳-99(V2)，设置有5个施氮水平——不施氮肥(N0)、正常施氮肥量的0.5倍(N1)、正常施肥量(N2)、正常施氮量的1.5倍(N3)和正常施氮量的2倍(N4)。不同的品种和施氮水平使水稻的长势以及产量之间存在差异，即有一定的梯度，使得在建立相对植被指数模型时避免所有的值有相似，使得建立的模型拥有更好普适性。2017年生长季的水稻播种时间为5月20日，移栽期为6月22日，收割时间为11月24日。种植密度为25 cm×23 cm。除品种和施氮量的不同外，其他种植条件均和当地种植水稻管理水平一致。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   实验田位置

Fig.1   Location of the field experiment


2.2　无人机成像高光谱数据获取与处理

本研究选用大疆Matrice 600 Pro 无人机(图3)，该型号无人机最大飞行高度为2.5 km，最大载重重量6 kg，续航时间大致为15~25 min。高光谱成像仪使用Rikola高光谱相机，该相机能够获取地物的从可见光到近红外的反射辐射值(波长范围500~900 nm，共有62个波段，半波宽为8 nm)，在100 m高度时地物的空间分辨率为6.5 cm，获取的每一幅高光谱影像大小为1 010×1 010像素。为确保数据质量，影像获取时间集中在水稻的几个关键生育期且当天为少云及微风的天气状况。每次的飞行航线固定，飞行高度固定为200 m，高光谱相机的曝光时间视当天的光照条件进行调整，飞行过程中相机获取的影像被实时存储在内存卡当中。在获取原始数据后，需进行光晕校正、畸变校正、暗电流校正和波段配准等一系列操作。除波段配准外，其他操作均在Rikola 高光谱成像仪配套的处理软件中进行。经过光晕、畸变和暗电流校正后，原始DN值影像被转为辐射值影像，可以使用ENVI、ArcGIS等软件做进一步处理，图4为获取的高光谱影像。根据水稻的实际生育期，从2017年7月28日至10月24日中选择了几个关键生育期的高光谱影像进行分析——分蘖期、拔节期、孕穗期、抽穗期、灌浆期和蜡熟期。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   研究区实验设计信息

Fig.2   Research area experimental design


图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   无人机高光谱平台

Fig.3   UAV hyperspectral platform


图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   无人机高光谱平台获取的高光谱数据立方体

Fig.4   Hyperspectral data cube acquired by the UAV hyperspectral platform


2.3　产量获取

实验田共22个小区，其中1个作为参考小区，每个小区3个取样点，选择长势均匀的3×3穴进行取样，对应高光谱影像6×6个像元点。采样后进行烘干、脱粒和测产等操作，产量单位均为kg/hm2。

2.4　方　法

2.4.1　相对光谱指数与相对产量的构建

为有效解决不同时期的植被指数受到的不同大气条件、光照条件和背景值的影响，提出相对光谱指数与相对产量的方法，即选择一块长势均匀的田块作为参考田块并计算出其平均光谱指数和平均单产，然后计算研究区除参考田块外63个采样点所包含的6×6个像元点的平均光谱指数，将各个田块中采样点的光谱指数除以相同时期参考田块的平均光谱指数得到相对光谱指数，63个采样点的产量也以同样的方法得到相对产量；最后综合使用多时期的相对光谱指数和相对产量建立估产模型，在以往的估产研究中选择了许多不同的植被指数建立估产模型[15,19]，但NDVI与水稻、小麦等谷物的产量呈现良好的线性关系[20,21]，所以本研究选择NDVI型光谱指数即归一化光谱指数(Normalized Difference Spectral Index, NDSI)作为研究变量，并使用多元线性回归模型 (Multiple Linear Regression, MLR)建立相对光谱变量与相对产量间的相关关系，其计算公式如下：

NDSI=λ1-λ2λ1+λ2
RNDSI=NDSINDSIR
RY=YYR

其中:λ1为高光谱影像波段1的反射辐亮度，λ2为高光谱影像波段2的反射辐亮度，RNDSI为相对归一化光谱指数，RNDSIR为参考田块的相对归一化光谱指数，Y为像元点实测产量，YR为参考产量，RY为相对产量。

2.4.2　确定最优相对植被指数

无人机高光谱遥感的最大优势是其波段连续性强、光谱数据量大，能够及时有效地宏观监测作物群体信息[22,23,24]。为更好地利用波长包含的信息，本研究使用任意两个高光谱影像波段进行组合，构建相对光谱指数并分析其与相对产量的相关性，并根据生育期的不同，择优选择光谱波段构建最佳相对光谱指数[25,26]。

2.4.3　评价指标

针对相对光谱指数与产量的相关性，本研究使用皮尔逊相关系数(Pearson Correlation Coefficient, r)评价其相关性的优劣。在使用多元回归模型建立不同水稻生育期组合与相对产量模型时，采用决定系数(Coefficient of Determination, R2)和均方根误差(Root Mean Square Error, RMSE)作为评判模型优劣的指标，此外模型验证额外使用相对误差(Relative Error, RE)来评估模型的估产精度。

3 结果分析

3.1　最优相对光谱指数的选择

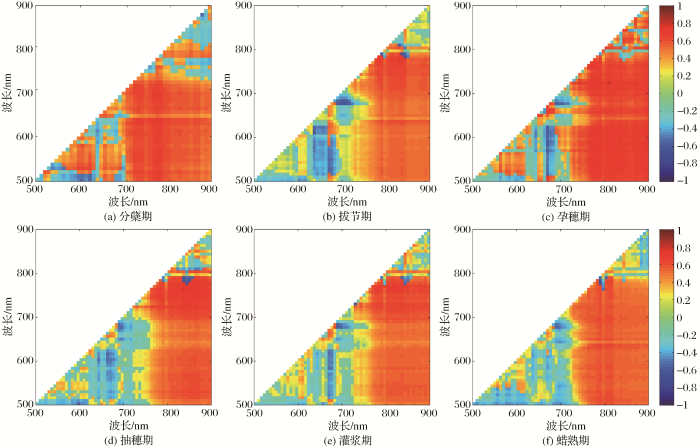
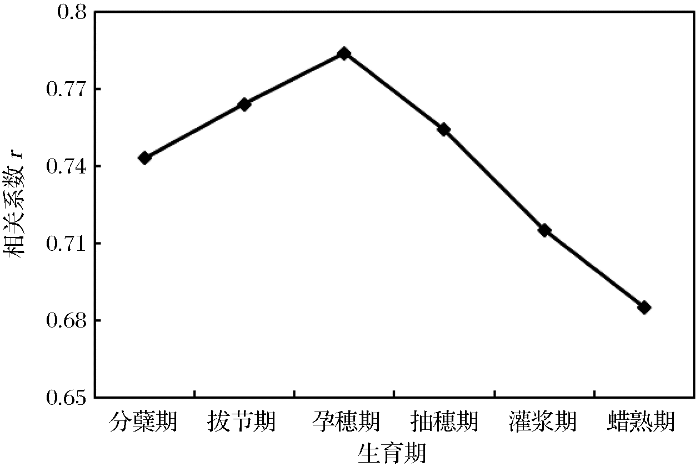
依据2.4.2节中的介绍，使用所有可能的波段组合构建不同时期RNDSI并分析其与相对产量间的相关关系(图5)。由于分蘖期的高光谱影像设置为了49个波段，所以图5（a）显示效果与其他几个生育期存在一定差异，可以看出，在分蘖期700~800 nm、650~700 nm波段构建的RNDSI与相对产量相关性较为密切，拔节期800~850 nm、700~800 nm波段构建的RNDSI与相对产量相关性较好，孕穗期750~850 nm、700~750 nm波段构建的RNDSI与相对产量相关性较强，抽穗期的RNDSI与相对产量相关性较强的波段范围为800~900 nm、700~800 nm，灌浆期为800~850 nm、700~800 nm，蜡熟期为750~800 nm、700~750 nm。可以发现，敏感波段均集中在红光、红边以及近红外波段。将每个生育期的最优RNDSI波段组合与相关系数挑选出来进行比较分析(表1和图6)，RNDSI与相对产量的相关性从分蘖期到孕穗期逐渐升高并在孕穗期达到最大，而后逐渐减低在蜡熟期达到最低，其波段组合与相关系数为分别为rRNDSI[784,635]=0.743，rRNDSI[807,744]=0.764，rRNDSI[784,712]=0.784，rRNDSI[816,736]=0.752，rRNDSI[816,740]=0.715，rRNDSI[792,748]=0.685，孕穗期的相对光谱变量与产量关系最为密切，下文分别使用这6个最佳波段组合建立水稻不同生育期组合估产模型。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   不同波段组合的相对光谱指数RNDSI与相对产量相关系数图

Fig.5   Correlation coefficient between relative spectral index RNDSI and relative yield in different band combinations


表1   水稻不同生育期RNDSI的最佳波段组合

Table 1  Optimal band combination of RNDSI in different growth stages of rice

时间水稻生育期RNDSI最优组合波段
20170728分蘖期635、 784
20170823拔节期744、 807
20170908孕穗期712、 784
20170919抽穗期736、 816
20171003灌浆期740、 816
20171024蜡熟期748、 792

新窗口打开| 下载CSV


图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   最佳RNDSI和相对产量的相关系数随生育期变化特征

Fig.6   The correlation coefficient between optimal RNDSI and relative yield varies with growth period


3.2　不同生育期组合模型

由于不同的水稻生育期组合有多种形式，所以采用穷举法列举出所有可能的组合形式建立拟合方程并进行分析选择最优估产模型。

3.2.1　单生育期估产模型

单一生育期估产是最简单的估产模型，其具有模型结构简单、计算方便等优点，但一般估产精度较差，表2给出了利用不同生育期的最佳RNDVI建立的单一生育期水稻估产模型。

表2   单一生育期估产模型

Table 2  Estimation models with single growth stage

生育期拟合方程R2RMSE(kg/hm2)
分蘖期(Tillering Stage)TSy=-0.61+1.59x10.55329.19
拔节期(Jointing Stage)JSy=0.48+0.50x20.58317.65
孕穗期(Booting Stage)BSy=-0.37+1.36x30.61305.51
抽穗期(Heading Stage)HSy=0.40+0.56x40.57323.15
灌浆期(Filling Stage)FSy=0.55+0.43x50.51344.28
蜡熟期(Ripening Stage)RSy=0.63+0.35x60.47358.86

注：x1表示分蘖期RNDSI[784,635]，x2表示拔节期RNDSI[807,744]，x3表示孕穗期RNDSI[784,712]，x4表示抽穗期RNDSI[816,736]，x5表示灌浆期RNDSI[816,740]，x6表示成熟期RNDSI[792,748]

新窗口打开| 下载CSV


由表2可知，孕穗期的RNDSI[784,712]可建立水稻单生育期最优估产模型R2=0.61，RMSE=305.51 kg/hm2，该线性拟合方程为：

y=-0.37+1.36x3

即：

YE=(-0.37+1.36×RNDSI[880,712](BS))×Y S

其中：YE是水稻预测单产(Estimation Yield)，YR是水稻标准单产(Reference Yield)。

3.2.2　两个生育期组合

由表3可以得出，分蘖期RNDSI[784,635]和孕穗期RNDSI[784,712]组合为两个生育期组合最优估产模型，R2=0.69，RMSE=273.09 kg/hm2。

表3   两个生育期组合估产模型

Table 3  Estimation models with two growth stages

生育期组合拟合方程R²RMSE(kg/hm2)
TS，JSy=-0.23+0.89x1+0.31x20.68279.48
TS，BSy=-0.74+0.82x1+0.89x30.69273.09
TS，HSy=-0.35+0.95x1+0.36x40.69273.63
TS，FSy=-0.32+1.05x1+0.25x50.66287.10
TS，RSy=-0.36+1.13x1+0.21x60.67284.11
JS，BSy=-0.11+0.26x2+0.83x30.68277.16
JS，HSy=0.34+0.30x2+0.32x40.68278.40
JS，FSy=0.46+0.35x2+0.17x50.61307.51
JS，RSy=0.47+0.37x2+0.13x60.61306.99
BS，HSy=-0.16+0.87x3+0.27x40.66286.15
BS，FSy=-0.18+1.01x3+0.15x50.64295.91
BS，RSy=-0.19+1.03x3+0.14x60.65290.84
HS，HSy=0.41+0.40x4+0.15x50.59316.73
HS，RSy=0.40+0.40x4+0.15x60.61306.01
FS，RSy=0.54+0.28x5+0.16x60.55330.61

新窗口打开| 下载CSV


YE=(-0.74+0.82×RNDSI[784,635](TS)+0.89× RNDSI[784,712](BS))×Y S

3.2.3 3个生育期组合

由表4可以得出，分蘖期RNDSI[784,635]、拔节期RNDSI[807,744]和抽穗期RNDSI[816,736]为3个生育期组合估产最优估产模型，R2=0.73，RMSE=255.05 kg/hm2。

表4   3个生育期组合估产模型

Table 4  Estimation models with three growth stages

生育期组合拟合方程R²RMSE(kg/hm2)
TS, JS, BSy=-0.47+0.64x1+0.19x2+0.62x30.72258.34
TS, JS, HSy=-0.18+0.69x1+0.20x2+0.25x40.73255.05
TS, JS, FSy=-0.20+0.84x1+0.22x2+0.12x50.69273.39
TS, JS, RSy=-0.21+0.87x1+0.21x2+0.12x60.70269.67
TS, BS, HSy=-0.53+0.74x1+0.55x3+0.21x40.72259.54
TS, BS, FSy=-0.57+0.77x1+0.67x3+0.11x50.71267.29
TS, BS, RSy=-0.56+0.77x1+0.65x3+0.12x60.72261.17
TS, HS, FSy=-0.31+0.92x1+0.28x4+0.075x50.70271.85
TS, HS, RSy=-0.27+0.88x1+0.25x4+0.11x60.71263.01
TS, HS, RSy=-0.29+1.00x1+0.14x5+0.13x60.68276.86
JS, BS, HSy=0.0070+0.22x2+0.54x3+0.20x40.71265.77
JS, BS, FSy=-0.098+0.25x2+0.81x3+0.020x50.68277.02
JS, BS, RSy=-0.072+0.22x2+0.77x3+0.060x60.69274.76
JS, HS, FSy=0.32+0.35x2+0.40x4-0.11x50.69275.64
JS, HS, RSy=0.35+0.28x2+0.30x4+0.040x60.68277.45
JS, FS, RSy=0.46+0.31x2+0.11x5+0.090x60.62303.37
BS, HS, FSy=-0.14+0.84x3+0.24x4+0.030x50.66285.89
BS, HS, RSy=-0.084+0.75x3+0.21x4+0.092x60.68279.96
BS, FS, RSy=-0.14+0.94x3+0.071x5+0.11x60.65289.28
HS, FS, RSy=0.41+0.38x4+0.039x5+0.14x60.61305.69

新窗口打开| 下载CSV


YE=(-0.18+0.69×RNDSI[784,635](TS)+0.20×RNDVI[807,744] (JS)+0.25×RNDVI[816,736] (HS))×Y S

3.2.4 4个生育期组合

由表5可以得出，分蘖期RNDSI[784,635]、拔节期RNDSI[807,744]、孕穗期RNDSI[784,712]和抽穗期RNDSI[816,736]为4个生育期组合最优估产模型，R2=0.74，RMSE=248.97 kg/hm2。

表5   4个生育期组合估产模型

Table 5  Estimation models with four growth stages

生育期组合拟合方程R²RMSE(kg/hm2)
TS, JS, BS, HSy=-0.34+0.59x1+0.16x2+0.37x3+0.18x40.74248.97
TS, JS, BS, FSy=-0.45+0.64x1+0.17x2+0.58x3+0.028x50.73258.07
TS, JS, BS, RSy=-0.43+0.67x1+0.14x2+0.54x3+0.072x60.73254.74
TS, JS, HS, FSy=-0.18+0.67x1+0.24x2+0.32x4-0.089x50.74253.26
TS, JS, HS, RSy=-0.18+0.70x1+0.17x2+0.22x4+0.053x60.74253.23
TS, JS, FS, RSy=-0.21+0.85x1+0.18x2+0.064x5+0.094x60.70268.31
TS, BS, HS, FSy=-0.52+0.73x1+0.54x3+0.20x4+0.013x50.72259.49
TS, BS, HS, RSy=-0.45+0.72x1+0.45x3+0.16x4+0.084x60.73253.93
TS, BS, FS, RSy=-0.53+0.76x1+0.60x3+0.037x5+0.10x60.72260.69
TS, HS, FS, RSy=-0.29+0.89x1+0.27x4-0.017x5+0.12x60.71262.94
JS, BS, HS, FSy=-0.040+0.28x2+0.58x3+0.30x4-0.14x50.72261.31
JS, BS, HS, RSy=0.017+0.21x2+0.53x3+0.19x4+0.025x60.71265.37
JS, BS, FS, RSy=-0.080+0.22x2+0.79x3-0.014x5+0.064x60.69274.70
JS, HS, FS, RSy=0.32+0.33x2+0.39x4-0.15x5+0.060x60.69273.32
BS, HS, FS, RSy=-0.10+0.77x3+0.24x4-0.043x5+0.10x60.68279.54

新窗口打开| 下载CSV


YE=(-0.34+0.58×RNDSI[784,635](TS)+0.16×RNDSI[807,744](JS)+0.37×RNDSI[784,712](BS)+0.18×RNDSI[816,736](HS))×Y S

3.2.5 5个生育期组合

由表6可以得出，分蘖期RNDSI[784,635]、拔节期RNDSI[807,744]、孕穗期RNDSI[784,712]、抽穗期RNDSI[816,736]和灌浆期RNDSI[816,740]为5个生育期组合最优估产模型，R2=0.75，RMSE=246.05 kg/hm2。

表6   5个生育期组合估产模型

Table 6  Estimation models with five growth stages

生育期组合拟合方程R²RMSE(kg/hm2)
TS, JS, BS, HS, FSy=-0.36+0.57x1+0.21x2+0.41x3+0.25x4-0.11x50.75246.05
TS, JS, BS, HS, RSy=-0.33+0.61x1+0.13x2+0.35x3+0.16x4+0.041x60.75247.84
TS, JS, BS, FS, RSy=-0.44+0.66x1+0.14x2+0.55x3-0.013x5+0.075x60.73254.68
TS, JS, HS, FS, RSy=-0.19+0.69x1+0.21x2+0.30x4-0.12x5+0.073x60.74249.96
TS, BS, HS, FS, RSy=-0.48+0.73x1+0.48x3+0.20x4-0.057x5+0.099x60.74253.11
JS, BS, HS, FS, RSy=-0.028+0.26x2+0.56x3+0.29x4-0.17x5+0.053x60.72259.68

新窗口打开| 下载CSV


YE=(-0.36+0.57×RNDSI[784,635](TS)+0.21×RNDSI[807,744](JS)+0.41×RNDSI[784,712](BS)+0.25×RNDSI[816,736](HS)-0.11×RNDSI[816,740](FS))×Y S

3.2.6 所有生育期组合

所有生育期组合的估产模型，R2=0.76 RMSE=243.49 kg/hm2。

YE=(-0.35+0.58×RNDSI[784,635](TS)+0.18×RNDSI[807,744](JS)+0.39×RNDSI[784,712](BS)+0.24×RNDSI[816,736](HS)-0.14×RNDSI[816,740](FS)+0.064×RNDSI[792,748](RS))×Y S

3.3　回归模型方程的显著性检验

当模型中组合的生育期个数大于3以后获得的多生育最佳组合模型的R2和RMSE并未随着组合生育期数量的增加而显著增加和减小。过多的生育期组合增加了模型的复杂程度，过少的生育期则影响估产精度，所以分别对所有不同生育期数量的最佳组合模型进行F检验，若均达到0.01显著水平时，则选择较低的RMSE和较少的生育期组合作为本研究的最佳估产模型。综合表7的评估参数，认为4个生育期组合估产模型是最理想的，所以得出结论公式(8)为水稻多生育期组合的最优估产模型。

表7   模型评估参数

模型R2RMSE(kg/hm2)F是否达到0.01显著水平
y=-0.37+1.36x30.61305.5197.39是
y=-0.74+0.82x1+0.89x30.69273.0967.49是
y=-0.18+0.69x1+0.20x2+0.25x40.73255.0553.60是
y=-0.34+0.59x1+0.16x2+0.37x3+0.18x40.74248.9742.19是
y=-0.36+0.57x1+0.21x2+0.41x3+0.25x4-0.11x50.75246.0534.24是
y=-0.35+0.58x1+0.18x2+0.39x3+0.24x4-0.14x5+0.064x60.76243.4928.82是

新窗口打开| 下载CSV


3.4　模型验证

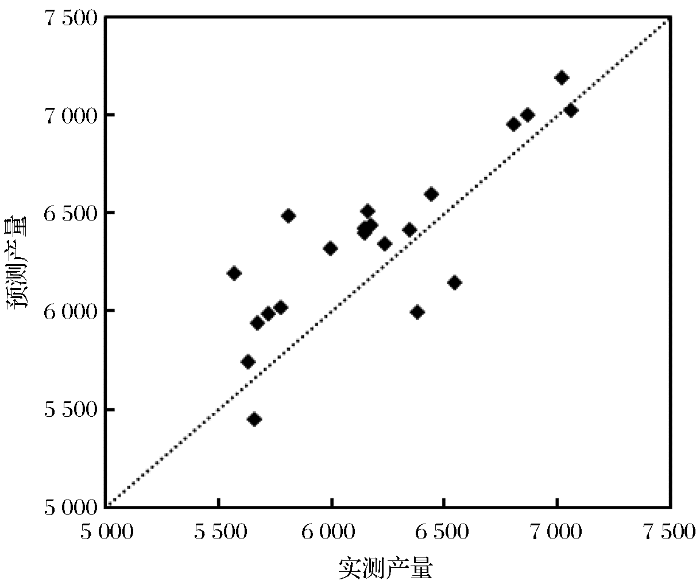
为评估上述提出的多生育期相对变量估产方法的准确性，将63个采样点随机分为两部分，其中42个采样点用来建模，21个采样点进行模型验证，依据前文所述使用分蘖期、拔节期、孕穗期和抽穗期4个生育期组合建立估产模型：

YE=(-0.44+0.65×RNDSI[784,635](TS)+0.16×RNDSI[807,744](JS)+0.34×RNDSI[784,712](BS)+0.26×RNDSI[816,736](HS))×Y S

R2=0.77，验证模型的平均相对误差绝对值达到了4.31%，RMSE=306.19 kg/hm2，模型结果较为理想。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   模型验证实测产量与预测产量对比

Fig.7   Comparison between measured yield and predicted yield


3.5　估产结果制图

根据上述模型绘制了2017年研究区的产量空间分布图，对比图2研究区实验设计信息，由图可以明显看到不同施氮量田块间产量的差异，并且图中所展示出的产量与田块的实测平均产量也相一致。根据此图可以提早发现产量异常值区域，例如施氮量不足、病虫害等情况，提早进行预防与防治，使产量维持在正常水平，确保粮食安全。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   研究区水稻产量空间分布图

Fig.8   Spatial distribution map of rice yield


4 结论与讨论

4.1　讨　论

水稻估产需要多生育期的遥感数据，但是无人机每次获取的遥感数据条件不一致，例如获取时间、天气条件和稻田背景均不一致(水稻前期背景是水土混合物，之后背景会有浮萍)等。如果想获得绝对准确的反射率计算植被指数，则需要精准的二向反射校正、直接辐射和散射辐射影响校正和背景差别校正。事实上，利用不同生育期反射率计算的植被指数忽略了以上影响，因而Matsushita等[27]指出植被指数NDVI在复杂多变的大气条件和冠层背景条件下以及其开环的结构（没有反馈调节因子）使得减弱的噪音量并不理想。考虑到无人机每次获取数据虽然存在大气条件、光照条件差异以及稻田背景不一致的问题，但是对于同一景数据的不同田块的获取条件是一致的，即具有相同的辐射、大气、太阳高度角等外界条件和相似的背景条件，因此将其中一块田块作为基准田块，借助于比值形式的优势，计算相对光谱变量，进一步消除外界条件对植被反射率的影响，结果证明了该方法的有效性。

较多的研究指出EVI耦合了抗大气植被指数(Atmospherically Resistant Vegetation Index, ARVI)和土壤调节植被指数(Soil Adjusted Vegetation Index, SAVI)，使得同时减小了大气和土壤背景对真实反射率的影响并避免了基于比值的植被指数的饱和问题[28]，但公式中存在的非比值项使观测时的几何形态和太阳高度角随地形的变化更加敏感[29]，这些非比值项也不适用于本研究提出的相对光谱变量，本研究利用NDVI简单比值的形式消除上述大气和植被背景对反射率的影响，所以研究中未考虑EVI。

由于氮素是水稻生长关键的营养元素之一，且不同地域土壤氮素水平差异较大[30]，本实验通过设置一系列从低到高不同梯度的氮素实验,能够更加有效地模拟不同地域水稻的真实生长情况，对于最终的估产模型而言，也能在一定程度上提高模型在不同氮素水平下的鲁棒性。

尺度效应是定量遥感研究中的科学核心问题[31]，Tian等[32]也曾指出当一个植被类型中混入其他植被类型时会产生较大的反演误差。而本研究假设提取出的6×6个连续相邻像元均为纯水稻植株像元，这明显是一个理想化的结果，提取的像元中必然包含其他背景值例如相邻的非采样水稻植株、杂草和土壤等，从而影响模型精度。

水稻不同生育期相对光谱变量与产量的相关性差异较大，从分蘖期至孕穗期相关性逐渐增加并在孕穗期达到最大之后逐渐减小，所以孕穗期与产量的相关性最高，是水稻估产的最佳生育期，已有研究结果也得出同样的结果[33]。主要原因一是因为孕穗期时水稻的叶面积指数达到最大值，冠层覆盖整个水田表面，高光谱成像仪获取到的像元均为纯水稻植株像元，二是该时期是水稻营养物质积累的巅峰时期与最终的产量关系密切。

估产使用的最优波段组合主要位于红边区域和近红外区域，红边区域是植被反射率显著变化的光谱区域，包含着大量植被信息。近红外区域是叶子健康状况最灵敏的标志，对植被差异及植物长势反应敏感，该结果与前人研究结果相一致[34]。除本研究使用的NDVI型相对植被指数外，其他比值类型相对光谱指数是否与水稻产量存在相关性以及它们对估产准确性的影响需要做进一步研究。

4.2　结　论

成像高光谱无人机平台的应用打破了卫星遥感的时空分辨率限制，为精准农业提供了更加丰富的高光谱信息。在本研究提出了相对植被指数的概念，并使用RNDSI构建相对植被指数估产模型，不同生育期构建最佳RNDSI的波段略有不同，但主要分布在近红外和红边区域；在利用RNDSI估产时，使用分蘖期RNDSI[784,635]、拔节期RNDSI[807,744]、孕穗期RNDSI[784,712]和抽穗期RNDSI[816,736]组成的多元线性回归模型是多生育期估产的最优模型；通过对该模型进行验证，估产平均相对误差绝对值达到了4.31%。研究结果表明相对植被指数能一定程度消除大气和光照条件的差异以及背景影响，能够较为准确的估算水稻产量，为水稻遥感估产提供了一种新的思路。

参考文献

National Bureau of Statistics of the People's Republic of China. Main Data Bulletin of the Sixth National Population Census of China in 2010

Source

[J]. Chinese Journal of Family Planning, 2011, 54(8):511-512.

[本文引用: 1]

中华人民共和国国家统计局.

2010年第六次全国人口普查主要数据公报(第1号)

[J]. 中国计划生育学杂志, 2011, 54(8):511-512.

[本文引用: 1]

Huang J, Wang X, Li X, et al.

Remotely Sensed Rice Yield Prediction Using Multi-temporal NDVI Data Derived from NOAA's-AVHRR

[J]. PloS one, 2013, 8(8):e70816. doi:10.1371/Journal.pone.0070816.

[本文引用: 1]

National Bureau of Statistics of the People's Republic of China.

China Statistical Yearbook

2015[M]. Beijing: China Statistics Press, 2016.

[本文引用: 1]

中华人民共和国国家统计局. 中国统计年鉴2015[M]. 北京: 中国统计出版社, 2016.

[本文引用: 1]

Chen Jingsong, Huang Jianxi, Lin Hui, et al.

Rice Yield Estimation by Assimilation Remote Sensing into Crop Growth Model

[J]. Scientia Sinica Informationis, 2010, 40(S1): 173-183.

[本文引用: 1]

陈劲松, 黄健熙, 林珲, 等.

基于遥感信息和作物生长模型同化的水稻估产方法研究

[J]. 中国科学: 信息科学, 2010, 40(增刊1): 173-183.

[本文引用: 1]

Chen Zhongxin, Ren Jianqiang, Tang Huajun,et al. 2016.

Progress and Perspectives on Agricultural Remote Sensing Research and Applications in China

[J]. Journal of Remote Sensing, 2016，20(5): 748–767.

[本文引用: 1]

陈仲新, 任建强, 唐华俊,等.

农业遥感研究应用进展与展望

[J]. 遥感学报, 2016, 20(5):748-767.

[本文引用: 1]

Turner D, Lucieer A, Watson C.

An Automated Technique for Generating Georectified Mosaics from Ultra-high Resolution Unmanned Aerial Vehicle (UAV) Imagery, based on Structure from Motion (SfM) Point Clouds

[J]. Remote sensing, 2012, 4(5): 1392-1410.

[本文引用: 1]

Gao Lin, Yang Guijun, Yu Haiyang, et al.

Retrieving Winter Wheat Leaf Area Index based on Unmanned Aerial Vehicle Hyperspectral Remoter Sensing

[J]. Transactions of the Chinese Society of Agricultural Engineering, 2016, 32(22): 113-120.

[本文引用: 1]

高林, 杨贵军, 于海洋, 等.

基于无人机高光谱遥感的冬小麦叶面积指数反演

[J]. 农业工程学报, 2016, 32(22)：113-120.

[本文引用: 1]

Zhao Xiaoqing, Yang Guijun, Liu Jiangang, et al.

Estimation of Soybean Breeding Yield based on Optimization of Spatial Scale of UAV Hyperspectral Image

[J]. Transactions of the Chinese Society of Agricultural Engineering, 2017, 33(1): 110-116.

[本文引用: 1]

赵晓庆, 杨贵军, 刘建刚, 等.

基于无人机载高光谱空间尺度优化的大豆育种产量估算

[J]. 农业工程学报, 2017, 33(1)：110-116.

[本文引用: 1]

Yue J, Yang G, Li C, et al.

Estimation of Winter Wheat Above-ground Biomass Using Unmanned Aerial Vehicle-based Snapshot Hyperspectral Sensor and Crop Height Improved Models

[J]. Remote Sensing, 2017, 9(7): 1-19. doi:10.33901rs9070708.

[本文引用: 1]

Calderón R, Navas-Cortés J A, Lucena C, et al.

High-resolution Airborne Hyperspectral and Thermal Imagery for Early Detection of Verticillium Wilt of Olive Using Fluorescence, Temperature and Narrow-band Spectral Indices

[J]. Remote Sensing of Environment, 2013, 139: 231-245.

[本文引用: 1]

Hall F G, Strebel D E, Nickeson J E, et al.

Radiometric Rectification: Toward a Common Radiometric Response Among Multidate, Multisensor Images

[J]. Remote Sensing of Environment, 1991, 35(1): 11-27.

[本文引用: 1]

Yuan D, Elvidge C D.

Comparison of Relative Radiometric Normalization Techniques

[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 1996, 51(3): 117-126.

[本文引用: 1]

de Carvalho O A, Guimarães R F, Silva N C, et al.

Radiometric Normalization of Temporal Images Combining Automatic Detection of Pseudo-invariant Features from the Distance and Similarity Spectral Measures, Density Scatterplot Analysis, and Robust Regression

[J]. Remote Sensing, 2013, 5(6): 2763-2794.

[本文引用: 1]

Du Y, Teillet P M, Cihlar J.

Radiometric Normalization of Multitemporal High-resolution Satellite Images with Quality Control for Land Cover Change Detection

[J]. Remote Sensing of Environment, 2002, 82(1): 123-134.

[本文引用: 1]

Zhu Wanxue, Li Shiji, Zhang Xubo, et al.

Estimation of Winter Wheat Yield Using Optimal Vegetation Indices from Unmanned Aerial Vehicle Remote Sensing

[J]. Transactions of the Chinese Society of Agricultural Engineering, 2018, 34(11): 78-86.

[本文引用: 2]

朱婉雪, 李仕冀, 张旭博,等.

基于无人机遥感植被指数优选的田块尺度冬小麦估产

[J]. 农业工程学报, 2018, 34(11):78-86.

[本文引用: 2]

Ouyang Ling, Mao Dehua, Wang Zongming, et al.

Analysis Crops Planting Structure and Yield based on GF-1 and Landsat 8 OLI Images

[J]. Transactions of the Chinese Society of Agricultural Engineering, 2017, 33(11): 147-156.

[本文引用: 1]

欧阳玲, 毛德华, 王宗明,等.

基于GF-1与Landsat 8 OLI影像的作物种植结构与产量分析

[J]. 农业工程学报, 2017, 33(11):147-156.

[本文引用: 1]

Liu Huanjun, Meng Linghua, Zhang Xinle, et al.

Estimation Model of Cotton Yield with Time Series Landsat Images

[J]. Transactions of the Chinese Society of Agricultural Engineering, 2015, 31(17): 215-220.

[本文引用: 1]

刘焕军, 孟令华, 张新乐, 等.

基于时间序列 Landsat 影像的棉花估产模型

[J]. 农业工程学报, 2015, 31(17)：215-220.

[本文引用: 1]

Ren Jianqing, Chen Zhongxin, Zhou Qingbo, et al.

MODIS Vegetation Index Data Used for Estimating Corn Yield in USA

[J]. Journal of Remote Sensing, 2015, 19(4): 568-577.

[本文引用: 1]

任建强, 陈仲新, 周清波,等.

MODIS 植被指数的美国玉米单产遥感估测

[J]. 遥感学报, 2015, 19(4): 568-577.

[本文引用: 1]

Liu Jiaodi, Cao Weibin, Li Hua, et al.

The Research of Cotton Yield Estimation base on Vegetation Index Using Remote Sensing in Xingjian

[J]. Journal of Shihezi University (Natural Science Edition), 2011, 29(2): 153-157.

[本文引用: 1]

刘姣娣, 曹卫彬, 李华, 等.

基于植被指数的新疆棉花遥感估产模型研究

[J]. 石河子大学学报(自然科学版), 2011, 29(2): 153-157.

[本文引用: 1]

Siyal A A, Dempewolf J, Becker-Reshef I.

Rice Yield Estimation Using Landsat ETM+ Data

[J]. Journal of Applied Remote Sensing, 2015, 9(1): 095986. doi:10.1117/1.JRS.9.095986.

[本文引用: 1]

Tucker C J, Holben B N, Elgin Jr J H, et al.

Relationship of Spectral Data to Grain Yield Variation

[J]. Photogrammetric Engineering and Remote Sensing, 1980, 46(5): 657-666.

[本文引用: 1]

Pei Haojie, Feng Haikuan, Li Changchun, et al.

Remote Sensing Monitoring of Winter Wheat Growth with UAV based on Comprehensive Index

[J]. Transactions of the Chinese Society of Agricultural Engineering, 2017, 33(20): 74-82.

[本文引用: 1]

裴浩杰, 冯海宽, 李长春, 等.

基于综合指标的冬小麦长势无人机遥感监测

[J]. 农业工程学报, 2017， 33(20): 74-82.

[本文引用: 1]

Du M, Noguchi N.

Monitoring of Wheat Growth Status and Mapping of Wheat Yield’s Within-field Spatial Variations Using Color Images Acquired from UAV-camera System

[J]. Remote Sensing, 2017, 9(3): 289. doi:10.3390/rs9030289.

[本文引用: 1]

Luna I, Lobo A.

Mapping Crop Planting Quality in Sugarcane from UAV Imagery: A Pilot Study in Nicaragua

[J]. Remote Sensing, 2016, 8(6): 500. doi:10.3390/rs8060500.

[本文引用: 1]

Kim M, Ko J, Jeong S, et al.

Monitoring Canopy Growth and Grain Yield of Paddy Rice in South Korea by Using the GRAMI Model and High Spatial Resolution Imagery

[J]. GIScience & Remote Sensing, 2017, 54(4): 534-551.

[本文引用: 1]

Guan K, Li Z, Rao L N, et al.

Mapping Paddy Rice Area and Yields over Thai Binh Province in Viet Nam from MODIS, Landsat, and ALOS-2/PALSAR-2

[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2018, 11(7): 2238-2252.

[本文引用: 1]

Matsushita B, Yang W, Chen J, et al.

Sensitivity of the Enhanced Vegetation Index (EVI) and Normalized Difference Vegetation Index (NDVI) to Topographic Effects: A Case Study in High-density Cypress Forest

[J]. Sensors, 2007, 7(11): 2636-2651.

[本文引用: 1]

Wang Zhengxing, Liu Chuang,

Huete Alfredo. From AVHRR-NDVI to MODIS-EVI: Advances in Vegetation Index Research

[J]. Acta Ecologica Sinica, 2003, 23(5): 979-987.

[本文引用: 1]

王正兴, 刘闯, Alfredo Huete.

植被指数研究进展: 从 AVHRR—NDVI 到 MODIS—EVI

[J]. 生态学报, 2003, 23(5): 979-987.

[本文引用: 1]

Garroutte E L, Hansen A J, Lawrence R L.

Using NDVI and EVI to Map Spatiotemporal Variation in the Biomass and Quality of Forage for Migratory Elk in the Greater Yellowstone Ecosystem

[J]. Remote Sensing, 2016, 8(5): 404. doi:10.3390/rs8050404.

[本文引用: 1]

Wang Z, Zhang X, Liu L, et al.

Evaluating the Effects of Nitrogen Deposition on Rice Ecosystems Across China

[J]. Agriculture, Ecosystems & Environment, 2019,206617:1-11. doi:10.1016/j.agee.2019.106617.

[本文引用: 1]

Li X, Wang Y.

Prospects on Future Developments of Quantitative Remote Sensing

[J]. Acta Geographica Sinica, 2013, 68(9): 1163-1169.

[本文引用: 1]

Tian Y, Woodcock C E, Wang Y, et al.

Multiscale Analysis and Validation of the MODIS LAI Product: I. Uncertainty Assessment

[J]. Remote Sensing of Environment, 2002, 83(3): 414-430.

[本文引用: 1]

Zhou X, Zheng H B, Xu X Q, et al.

Predicting Grain Yield in Rice Using Multi-temporal Vegetation Indices from UAV-based Multispectral and Digital Imagery

[J]. Isprs Journal of Photogrammetry & Remote Sensing, 2017, 130:246-255.

[本文引用: 1]

Verger A, Vigneau N, Chéron C, et al.

Green Area Index from an Unmanned Aerial System over Wheat and Rapeseed Crops

[J]. Remote Sensing of Environment, 2014, 152:654-664.

[本文引用: 1]

/

〈 〉